从零开始发明 AC 自动机
Published:
AC 自动机是一种多模字符串匹配算法。
给你一个文本串 $S$ 和 $n$ 个模式串 $T_{1 \sim n}$,请你分别求出每个模式串 $T_i$ 在 $S$ 中出现的次数。
$1 \le n \le 2 \times {10}^5$,$T_{1 \sim n}$ 的长度总和不超过 $2 \times {10}^5$,$S$ 的长度不超过 $2 \times {10}^6$。
下文中涉及时间复杂度的部分,$n$ 为模式串长度之和,$m$ 为文本串长度。
前置知识
- 字典树:[Luogu P8306]【模板】字典树。
- KMP:[Luogu P3375]【模板】KMP(不必要,但是最好了解其思想)。
- 自动机(DFA)基本概念:https://oi-wiki.org/string/automaton/。
- 自动机五要素:
- 字符集 $\Sigma$。
- 状态集合 $Q$。
- 起始状态 $start$。
- 接收状态集合 $F$。
- 转移函数 $\delta$。$\delta(u,c)$ 中 $u,\delta(u,c) \in Q$,$c \in \Sigma$。
Step 1:AC 自动机基于字典树
有多个模式串,考虑有什么简单的结构能解决多个字符串的问题。不难想到哈希和字典树。
哈希可能会碰撞,且看起来跟自动机相关理论没什么关系,很难扩展。
字典树可以视作自动机。
建立字典树时间复杂度 $O(n)$。
int ins(string s) {
int u = 0;
for (auto ch : s) {
int c = ch - 'a';
if (!tr[u][c])
tr[u][c] = ++tot;
u = tr[u][c];
}
return u;
}
Step 2:fail 数组的定义
多模字符串匹配是单个模式串匹配的扩展,所以考虑 KMP。
KMP 算法可以视作自动机。基于字符串 $s$ 的 KMP 自动机接受且仅接受以 $s$ 为后缀的字符串。
那么 AC 自动机就应该是:基于字符串 $s_{1 \sim n}$ 的 AC 自动机接受且仅接受以 $s_{1 \sim n}$ 任意一个为后缀的字符串。
考虑在 Trie 上定义一个类似 KMP 中 next 数组的数组。
具体地,定义 $fail(u)$ 为 $u$ 表示的字符串 最长的 且 出现在 Trie 上的 真 后缀对应的状态。
在自动机上连上 $u$ 与 $fail(u)$ 的边,这条边被称为 fail 边。
从 OI-Wiki 偷一张图来解释:
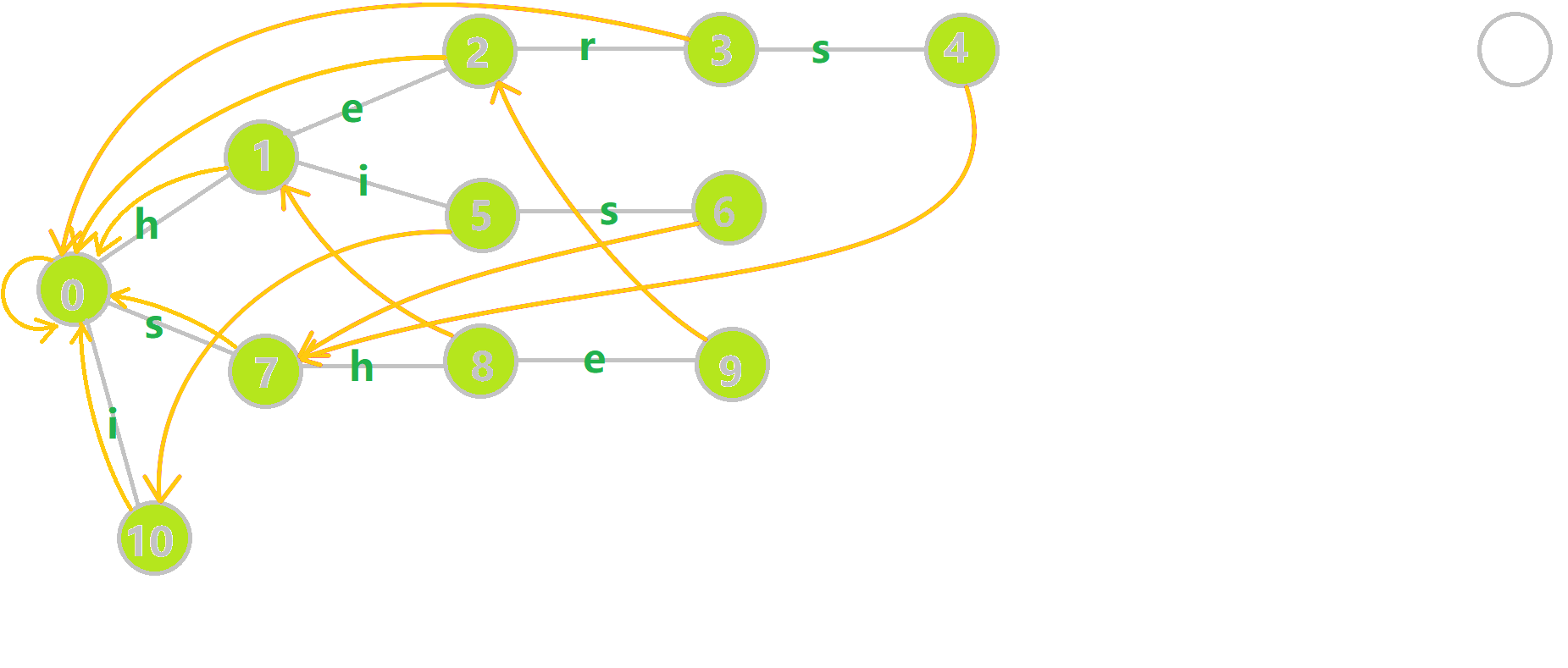
灰色边为 Trie,黄色边为 fail 边。
例如此图中 $9$ 号连到 $2$ 号,是因为 $\texttt{she}$ 出现在 Trie 上的最长真后缀为 $\texttt{he}$,即 $2$ 号。
不难发现,这个 $fail(u)$ 当 Trie 中只有一个模式串时,就是 KMP 的 next 数组(这里的 next 数组表示 border 长度)。
重要性质:fail 边形成一棵树。这是 KMP 的 fail 树的应用:[Luogu P5829]【模板】失配树。
Step 3:fail 如何求 & 构建 AC 自动机
自动机五要素:
- 字符集 $\Sigma$,为小写字母。
- 状态集合 $Q$,为 Trie 上的所有节点。
- 起始状态 $start$,为 Trie 的根节点 $0$。
- 接收状态集合 $F$,为所有模式串在 Trie 上的节点。
- 转移函数 $\delta$,下文着重讲解这一点。
以下 $tr$ 指原字典树。
若 $tr_{u,c}$ 存在,则 $\delta(u,c) = tr_{u,c}$,$fail(\delta(u,c)) = \delta(fail(u),c)$。
- 注意到 $fail(\delta(u,c))$ 基于 $fail(u)$,所以我们 BFS 求解 fail。
若 $tr_{u,c}$ 不存在:
- 若 $u$ 是根节点 $0$,则 $\delta(u,c) = 0$。
- 如果没有这一条,则 $0$ 的儿子的 $fail$ 会连到自身,不满足真后缀。
- 否则 $\delta(u,c) = \delta(fail(u),c)$。
最后一条的递归与 KMP 的不断跳 next 是相同的。关于这一点,我们可以看看 KMP 自动机的 $\delta$:
\[\delta(u,c) = \begin{cases} u+1 & c = s_{u+1} \\ 0 & c \ne s_{u+1} \land u = 0 \\ \delta(next(u),c) & c \ne s_{u+1} \land u \ne 0 \end{cases}\]再看看 AC 自动机的 $\delta$:
\[\delta(u,c) = \begin{cases} tr_{u,c} & tr_{u,c} \text{ exists} \\ 0 & tr_{u,c} \text{ does not exist} \land u = 0 \\ \delta(fail(u),c) & tr_{u,c} \text{ does not exist} \land u \ne 0 \end{cases}\]不能说十分类似,只能说是一模一样。
| 代码上,我们不用重新建一个自动机,直接按照 AC 自动机的 $\delta$ 改 Trie 的结构即可。时间复杂度 $O(n | \Sigma | )$。 |
// tr 原本为字典树
void bfs() {
queue<int> q;
for (int c = 0; c < 26; c++)
if (tr[0][c])
q.push(tr[0][c]);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int c = 0; c < 26; c++)
if (tr[u][c]) {
fail[tr[u][c]] = tr[fail[u]][c];
q.push(tr[u][c]);
} else
tr[u][c] = tr[fail[u]][c];
}
}
你非要新建一个自动机也不是不行。但是空间常数大一倍,没啥意义。
// tr 为字典树
// dt 指转移函数 delta
void bfs() {
queue<int> q;
for (int c = 0; c < 26; c++)
if (tr[0][c])
q.push(dt[0][c] = tr[0][c]);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int c = 0; c < 26; c++)
if (tr[u][c]) {
dt[u][c] = tr[u][c];
fail[dt[u][c]] = dt[fail[u]][c];
q.push(dt[u][c]);
} else
dt[u][c] = dt[fail[u]][c];
}
}
// 注意后文作匹配的时候要沿着 dt 而不是 tr
Step 4:多模字符串匹配
接下来我们就可以把文本串作为输入给到 AC 自动机。
用一个数组记录每一个节点被走过了多少次。
建出 fail 树,DFS 子树求和,保存在 $sum$ 数组。
此时 $sum_u$ 为 $u$ 对应的字符串被匹配到的次数。原因是 fail 树上,若一节点匹配上了,则其祖先也必然匹配。
第 $i$ 个模式串对应节点的子树和即为答案。
(这一段看具体代码更容易懂。)
总结 & 完整代码
- 建出 Trie 树,保存每个模式串在 Trie 上的位置。$O(n)$。
把 Trie 树改造为 AC 自动机,并求出 fail 数组,建出 fail 树。$O(n \Sigma )$。 - 把文本串作为输入给到 AC 自动机,在 fail 树上求和得到答案。$O(m)$。
| 空间复杂度为 $O(n | \Sigma | + m)$。 |
DFS 用了 lambda 表达式。以普通函数的形式写一个 DFS 也是没有问题的。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 2e5 + 5; // 模式串长度之和
int tr[MAXN][26], fail[MAXN], tot = 0;
int e[MAXN], sum[MAXN];
vector<int> G[MAXN];
int ins(string s) {
int u = 0;
for (auto ch : s) {
int c = ch - 'a';
if (!tr[u][c])
tr[u][c] = ++tot;
u = tr[u][c];
}
return u;
}
void bfs() {
queue<int> q;
for (int c = 0; c < 26; c++)
if (tr[0][c])
q.push(tr[0][c]);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int c = 0; c < 26; c++)
if (tr[u][c]) {
fail[tr[u][c]] = tr[fail[u]][c];
q.push(tr[u][c]);
} else
tr[u][c] = tr[fail[u]][c];
}
}
int main() { ios::sync_with_stdio(0); cin.tie(0);
int n; cin >> n; for (int i = 1; i <= n; i++) {
string s; cin >> s;
e[i] = ins(s);
}
bfs();
for (int u = 1; u <= tot; u++)
G[fail[u]].push_back(u);
string t; cin >> t;
int u = 0;
for (auto ch : t) {
int c = ch - 'a';
u = tr[u][c];
sum[u]++;
}
auto dfs = [&](int u, auto&& self) -> void {
for (auto v : G[u]) {
self(v, self);
sum[u] += sum[v];
}
};
dfs(0, dfs);
for (int i = 1; i <= n; i++)
cout << sum[e[i]] << '\n';
return 0;
}