AP E&M Chapter 11 Gauss’s Law
Published:
Flux
The flux $\Phi$ (通量) is defined as
\[\boxed{ \Phi = \int \vec{F} \cdot d\vec{A} }\]where $\vec{F}$ is vector field, and $d\vec{A}$ is defined as a vector with magnitude equal to $dA$ and direction perpendicular to the surface. 💡For open surfaces, the direction of $d\vec{A}$ can be chosen to point inward or outward. For closed surfaces, $d\vec{A}$ always points outward.
(Usually, this formula is written as $\Phi = \int_S \vec{F} \cdot d\vec{A}$, which implies that the integral is over the entire surface $S$)
If the flux is positive, it means field lines exit the surface, and vice versa.
Electric flux (电通量) is the flux when the vector field is an electric field:
\[\boxed{ \Phi_{\text{electric}} = \int \vec{E} \cdot d\vec{A} }\]Gauss’s Law
\[\colorbox{#424242}{$ \color{white}\boxed{ \Phi_{\text{electric}} = \oint \vec{E} \cdot d\vec{A} = \frac {Q_{\text{enclosed}}} {\varepsilon_0} } $}\]The symbol $\oint$ means that we integrate over a closed surface (which is called the gaussian surface (高斯面)).
At this link, there is a intuitive understanding for Gauss’s Law.
Coulomb’s Law only gives the electric field of an electrostatic point charge. However, Gauss’s Law is more general and can be used in any situation. That’s what makes it a law instead of a theorem.
Coulomb’s Law V.S. Gauss’s Law
💡 Coulomb $\implies$ Gauss
(Based on the principle of superposition for electric field)
Step 1: We need to prove the differential form of Gauss’s Law:
\[\boxed{\nabla \cdot \vec{E} = \frac \rho {\varepsilon_0}}\]Proof.
\[\vec{E}(\vec{r}) = \frac 1 {4\pi\varepsilon_0} \int \rho(\vec{r'}) \frac {\hat r} {|\vec{r} - \vec{r'}|^2} dV'\] \[\begin{aligned} \nabla \cdot \vec{E} &= \frac 1 {4\pi\varepsilon_0} \int \rho(\vec{r'}) \nabla \cdot \left( \frac {\hat r} {|\vec{r} - \vec{r'}|^2} \right) dV' \\ &= \frac 1 {4\pi\varepsilon_0} \int \rho(\vec{r'}) 4 \pi \delta(\vec{r} - \vec{r'}) dV' \\ &= \frac {\rho(\vec{r'})} {\varepsilon_0} \\ \end{aligned}\]where $\delta$ is the Dirac delta function.
$\square$
Step 2: We need to prove the integral form of Gauss’s Law from the differential form:
\[\oint \vec{E} \cdot d\vec{A} = \frac {Q_{\text{enc}}} {\varepsilon_0}\]Proof. According to Gauss’s Divergence Theorem (高斯散度定理):
\[\begin{aligned} \oint \vec{E} \cdot d\vec{A} &= \int_{\text{enclosed}} (\nabla \cdot \vec{E}) dV \\ &= \int \frac \rho {\varepsilon_0} dV \\ &= \frac {Q_{\text{enclosed}}} {\varepsilon_0} \\ \end{aligned}\]$\square$
Gauss $\implies$ Coulomb
(Based on the spheric symmetry of the electric field due to a point charge)
Use the same method as Example 11.3.
Insulators
Insulators (绝缘体) are materials that have no “free” electrons, so charge is not free to move within them. Consequently, all sorts of charge distributions are possible on nonconductors: You can put charge wherever you want to and it stays there.
Example 11.1: Infinite Plane
Calculate the electric field produced by an infinitely large sheet of charge with uniform charge density $+σ$ $\ce{C/m^2}$.
Method 1: Following the old way
Recall that the electric field of a uniformly charged disk with radius $a$ at a distance $d$ along the axis from its center is (from Example 10.12)
\[E = \frac {\sigma d} {2 \varepsilon_0} \left( \frac 1 d - \frac 1 {\sqrt{a^2 + d^2}} \right)\]An infinitely large sheet is the limit of a disk when the radius $a$ approaches infinity:
\[\begin{aligned} E &= \lim\limits_{a \to \infty} \frac {\sigma d} {2 \varepsilon_0} \left( \frac 1 d - \frac 1 {\sqrt{a^2 + d^2}} \right) \\ &= \frac \sigma {2 \varepsilon_0} \\ \end{aligned}\]Therefore, we can conclude that the electric field due to an infinite plane of charge with charge density $\sigma$ is:
\[\boxed{ E = \frac \sigma {2 \varepsilon_0} }\]Method 2: Use Gauss’s Law
We notice the charge distribution has planar symmetry. Therefore, we take a cylinder as the gaussian surface, and the cylinder is evenly divided by the plane.
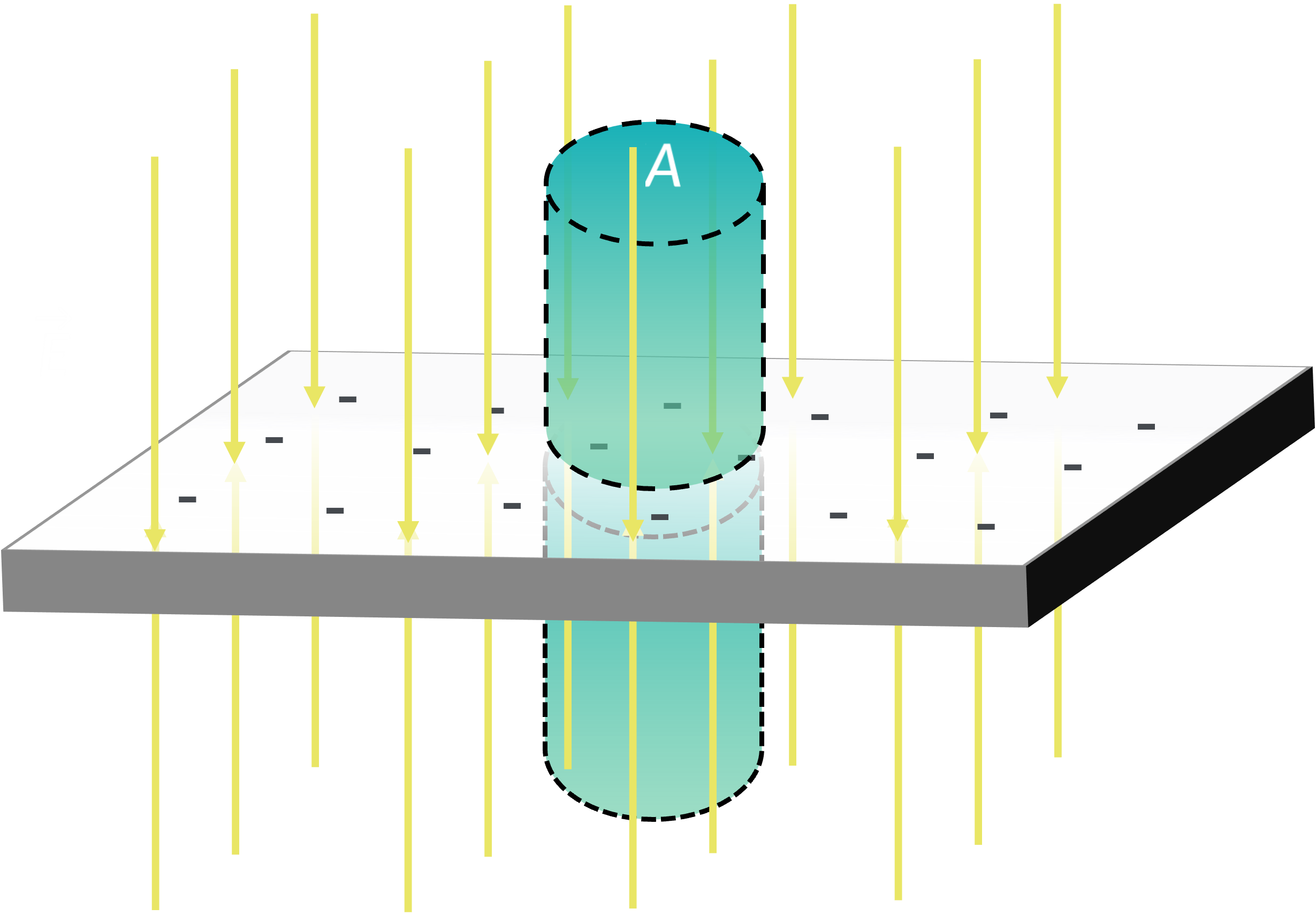
We get the same answer as above.
Example 11.2: Infinite Line
Calculate the electric field produced by an infinitely long line of charge of constant linear charge density $\lambda$ $\ce{C/m}$.
We notice the charge distribution has cylindrical symmetry. Therefore, we take a cylinder whose axis is along the line as the gaussian surface.
Example 11.3.0: Shell
Given a thin spherical shell of surface charge density $\sigma$ $\ce{C/m^2}$ and radius $R$, calculate the magnitude of
- (a) the electric field outside the shell and
- (b) the electric field inside the shell as functions of $r$, the distance from the center of the sphere.
We notice the charge distribution has spherical symmetry. Therefore, we take a sphere with radius $r$ as the gaussian surface.
\[\begin{aligned} \Phi &= \oint \vec{E} \cdot d\vec{A} \\ &= 4 \pi r^2 E \\ \end{aligned}\](a)
\[\begin{aligned} \Phi &= \frac Q {\varepsilon_0} \\ 4 \pi r^2 E &= \frac {\sigma 4 \pi R^2} {\varepsilon_0} \\ E &= \frac {\sigma R^2} {\varepsilon_0 r^2} \\ \end{aligned}\](b)
\[\begin{aligned} \Phi &= \frac Q {\varepsilon_0} \\ 4 \pi r^2 E &= 0 \\ E &= 0 \\ \end{aligned}\]Example 11.3.1: Gauss’s law for gravity
Gauss’s law for gravity (高斯重力定律):
\[\boxed{ \oint \vec{g} \cdot d\vec{A} = -4\pi G m_{\text{enclosed}} }\]From the Gauss’s law for gravity, we can derive the Shell theorem (壳层定理):
- A spherically symmetric body affects external objects gravitationally as though all of its mass were concentrated at a point at its center.
- If the body is a spherically symmetric shell (i.e., a hollow ball), no net gravitational force is exerted by the shell on any object inside, regardless of the object’s location within the shell.
Example 11.4
Consider an insulating sphere of radius $a$. Within the sphere the charge density is given by the equation $\rho(r) = br^3$. Calculate the electric field at a point $r_0$ with (a) $r_0 < a$, (b) $r_0 > a$, and (c) $r_0 = a$.
This question is relatively easy, so I’m not gonna put the answer here. However, this problem reveals an important principle:
As long as the volume charge density is finite, the electric field is continuous.
Example 11.5: Infinite Rod
An infinitely long nonconducting cylindrical rod of radius a has a linear charge density of $\lambda$ $\ce{C/m}$ distributed evenly through its volume. Calculate the electric field (a) outside and (b) inside the rod at a distance $R$ from its center.
This question is also easy, and answers are here:
(a)
\[E = \frac \lambda {2 \pi R \varepsilon_0}\](b)
\[E = \frac {\lambda R} {2 \pi \varepsilon_0 a^2}\]Conductors
Conductors (which, as far as Physics C is concerned, are equivalent to metals) have free electrons, so charge is free to move within them.
Static Equilibrium
Electrostatic equilibrium (静电平衡) occurs when the charges within a conductor are at rest, resulting in no net movement of charge. (Electrostatic equilibrium - Fiveable)
The electric field inside a conductor is zero in static equilibrium. 💡The electric field inside on the surface of a conductor can only be perpendicular to the surface.
\[\boxed{ \vec{E}_{\text{inside}} = 0 }\]An equivalent saying is the potential inside the conductor is a constant (or we can say the conductor is at a constant potential).
Take a gaussian surface inside the conductor. Because the electric field inside the conductor is always $0$, the electric flux through the gaussian surface is also $0$. Therefore, according to Gauss’s Law, we can derive that the charge enclosed by the gaussian surface is $0$.
If charge existed in the interior of the conductor, this would violate the statement above. Therefore, charge can exist only on the surface of a conductor.
Example 11.6
Suppose we have a hollow metal spherical shell of inner radius $a$ and outer radius $b$. A point charge $+Q$ is located in the center of the shell. The shell itself has a net charge of $+2Q$.
Find the charge distribution on the spherical shell.
Any gaussian surface inside the conductor contains the point charge and the inner surface of the shell. Because charge can only exist on the surface of the shell and the net charge enclosed by the gaussian surface is $0$, it means that the inner surface of the shell needs to contain a net charge of $-Q$. Therefore, the outer surface of the shell has to contain a net charge of $+3Q$.
