AP E&M Chapter 12 Capacitors
Published:
Intro to Capacitor (电容器)
Suppose two metal plates are placed face to face, and they are connected to a battery.
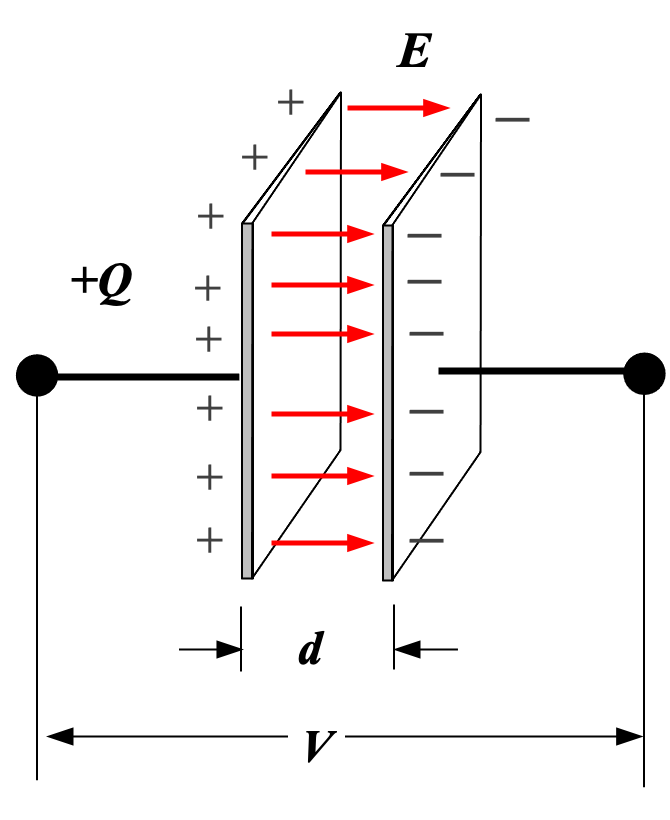
At first, the battery deposits positive charge on the left plate. Because like charges repel and unlike charges attract, positive charges on the right plate flow away, establishing a current. The new distribution of charges also creates a voltage between the two plates.
Suppose the battery is disconnected. The voltage between the two plates still exists, so it can be used as a battery. Therefore, a capacitor can store energy.
Capacitance
The capacitance (电容) of a capacitor is defined as the ratio of the charge accumulation to the voltage. It is a property of the capacitor itself, which means it does not depend on $Q$ or $V$.
\[\boxed{ C = \frac Q V }\]The unit of capacitance is farad (法拉), given by $1 \text{ farad} = 1 \ \ce{F} = \frac {1 \ \ce{C}} {1 \ \ce{V}}$.
Most real-life capacitors are in the range of microfarads $\text{mF}$ (微法), nanofarads $\mu\text{F}$ (纳法), picofarads $\text{pF}$ (皮法).
Example 12.1 Parallel Plate Capacitor
Calculate the capacitance of a parallel plate capacitor with plates of area $A$ separated by a distance $d$. Assume that the dimensions of the plates are much greater than the separation $d$ so that “edge effects” can be ignored.
Note: This solution assumes that the plates are separated by a vacuum.
Because edge effects are negligible, we assume the two plates of the capacitors are infinitely large sheets with uniform charge density.
Assume the plates have charges $+Q$ and $-Q$, respectively. We now need to calculate the voltage between the two plates. The charge density $\sigma$ is $\frac Q A$.
From Example 11.1, we know the electric field produced by an infinitely large sheet of charge with uniform charge density $+σ$ $\ce{C/m^2}$ is
\[\frac \sigma {2 \varepsilon_0}\]Between the two plates, the electric fields produced by the two plates add together:
\[E = - \frac \sigma {2 \varepsilon_0} + (- \frac \sigma {2 \varepsilon_0}) = - \frac \sigma {\varepsilon_0}\]The absolute value of voltage is the path integral of $\vec{E}$:
\[\begin{aligned} |V| &= \int_{\text{path between the plates}} \vec{E} \cdot d\vec{R} \\ &= \int_0^d E dR \\ &= Ed \\ &= \frac {\sigma d} {\varepsilon_0} \\ &= \frac {Qd} {A\varepsilon_0} \\ \end{aligned}\]An important step in the derivation is: (valid only for parallel plate capacitors)
\[\boxed{ |V| = Ed }\]Plug in the value for $V$ into $C = \frac Q V$:
\[\begin{aligned} C &= \frac Q V \\ &= \frac Q {\frac {Qd} {A\varepsilon_0}} \\ &= \frac {A \varepsilon_0} d \\ \end{aligned}\]The capacitance of parallel plate vacuum capacitor is:
\[\boxed{ C = \frac {A \varepsilon_0} d }\]Combinations of Capacitors
In Series
Capacitors in series (串联) store the same charge.
\[C = \frac Q V = \frac Q {\sum V_i} = \frac 1 {\sum \frac 1 {C_i}}\] \[\boxed{ C_{\text{equivalent}} = \frac 1 {\sum \frac 1 {C_i}} }\]In Parallel
Capacitors in parallel (并联) have the same voltage between the two sides.
\[C = \frac Q V = \frac {\sum Q_i} V = \sum C_i\] \[\boxed{ C_{\text{equivalent}} = \sum C_i }\]💡 Short-Circuit Created by Capacitors
What if a capacitor is connected directly to a battery?
- If the capacitor voltage just equals the source voltage, nothing happens.
- If the capacitor voltage is less than the source voltage or greater than the source voltage, an instantaneous infinite current will occur, resulting in a short-circuit effect.
Similar situations happen when:
- two capacitors with different voltages are directly connected
- a charged capacitor is connected to itself
Energy Stored in Capacitors
\[\begin{aligned} U &= \int dU \\ &= \int V dq \\ &= \int_0^Q \frac q C dq \\ &= \frac {Q^2} {2C} \end{aligned}\]Therefore, the energy stored in a capacitor is
\[\boxed{ U = \frac {Q^2} {2C} = \frac 1 2 CV^2 = \frac 1 2 QV }\]Dielectrics
When the plates of capacitor are separated by a dielectric material (介电质) instead of vacuum, the charge on each plate induces an opposite charge on the surface of the dielectric material, causing an increase in capacitance.
The new capacitance can be calculated by the formula
\[\boxed{ C = \kappa_D C_0 }\]where $\kappa_D$ is called the dielectric constant (相对介电常数) (which is a property of each dielectric material), and $C_0$ is the original capacitance.
The dielectric constant of vacuum is $1$.
Example 12.3 Capacitors with Dielectrics
\[\begin{aligned} C &= \kappa_D C_0 \\ &= \frac {\kappa_D A \varepsilon_0} d \\ \end{aligned}\]Calculate the capacitance of a parallel plate capacitor with plates of area $A$ separated by a distance $d$. Assume that the dimensions of the plates are much greater than the separation $d$. The volume between the plates is filled with a dielectric material of dielectric constant $\kappa_D$.
Therefore, the capacitance of a parallel plate capacitor with a dielectric is
\[\boxed{ C = \frac {\kappa_D A \varepsilon_0} d }\]