数据结构 5

9 minute read

Published: June 28, 2025

静态链分治

也叫树上启发式合并，俗称 DSU on tree，虽然我完全不知道为什么叫这个名字。

对于一棵树，$siz_u$ 是 $u$ 的子树大小，$hson_u$ 是 $u$ 的重儿子。静态链分治算法的核心是这样一个式子：

\[\sum\limits_{u=1}^n (siz_u - siz_{hson_u}) = O(n \log n)\]

即所有轻子树大小之和为 $O(n \log n)$。

这个是重链剖分的基本性质：从每个节点往根节点的方向走，每经过一条轻边则子树大小至少翻一倍。

（btw，如果是长链剖分的长儿子，这个式子算出来是 $O(n \sqrt n)$ 的。来源：树分治小记 - command_block）

接下来具体讲一下算法的用途和流程。

首先问题要可以离线。我们要对每个节点都计算出一个答案，并且这个答案基于一个 $info$ 可以算出，而且每个节点的 $info$ 可以由儿子的 $info$ 推过来。

但是 $info$ 如果不是 $O(1)$ 或者 log 级别的话，对于每个节点都维护一个 $info$ 是不现实的，需要资源复用。

这话还是很抽象，看一个例子。

静态链分治例题

CF208E Blood Cousins (Easy)

给你一片森林，每次给定参数 $u,k$，询问一个点 $u$ 与多少个点拥有共同的 $k$ 级祖先。
$n,m \le 10^5$。离线（但是题解区有一个在线的可持久化线段树做法）。

套路用静态链分治处理离线的单点询问，可以把询问挂到子树上。

我们首先求出 $u$ 的 $k$ 级祖先 $p$（LA 问题倍增即可），把询问挂在那里，变成 $p$ 有几个 $k$ 级后代。

但是 $k$ 级后代是个相对的概念，不适合静态链分治的全局统计。我们发现一个等价的说法，就是 $p$ 子树中深度为 $dep_p + k$ 的点的个数。

此时就和前面的模板题做法一致了。时间复杂度 $O(n \log n)$。

btw 这题线段树合并也可以做（也是 1log）。

P4149 [IOI 2011] Race (Easy)

给一棵树，每条边有权。求一条简单路径，权值和等于 $k$，且边的数量最小。
$n \le 2 \times 10^5$，值域 $10^6$。

超绝 IOI 水题。

套路用静态链分治处理离线的路径询问，可以把询问挂在 LCA 上。

和上一题一样，$\text{dis}(u,v)$ 是局部信息，先转成全局的信息方便统计。

熟悉的套路：$\text{dis}(u,v) = \text{dis}(1,u) + \text{dis}(1,v) - 2 \times \text{dis}(1, \text{LCA}(u,v))$。

开个桶，维护每个 $\text{dis}(1,u)$ 对应的最小 $dep$，和上面一样做法。$O(n \log n)$。

实现细节：为了防止出现两段路径 $u \rightsquigarrow v_1$ 和 $u \rightsquigarrow v_2$ 拼起来时 $v_1$ 和 $v_2$ 在同一子树内的情况，我们在加入轻子树 $info$ 之前，先遍历一遍轻子树算这棵子树和前面子树拼起来的答案，这一遍不记 $info$。（所以要写三个 DFS，预处理一个，静态链分治自身一个，算贡献前先算答案一个）

btw 这题点分治也可以做（也是 1log）。

CF741D Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths (Normal)

（据说是算法发明者出的题？）

一棵根为 $1$ 的树，每条边上有一个字符。一条简单路径被称为 Dokhtar-kosh 当且仅当路径上的字符经过重新排序后可以变成一个回文串。
求每个子树中最长的 Dokhtar-kosh 路径的长度。
$n \le 5 \times 10^5$，$\lvert \Sigma \rvert = 22$。（嗯真的是 $22$，不是我打错了）

重排是回文串，很明显跟异或是有关的。每个点 $u$ 处维护一个桶，桶的每个元素是一个长为 $\lvert \Sigma \rvert$ 的二进制数，代表 $u$ 往下的路径上的颜色数 $\bmod 2$。

然后和上面那题一样做法，但是统计答案的时候要枚举哪一位异或之后是 $1$（当然还有一位也没有的情况），总共 $\lvert \Sigma \rvert + 1$ 个情况，复杂度多一个 $O(\lvert \Sigma \rvert)$。

最终时间复杂度 $O(\lvert \Sigma \rvert n \log n)$，空间复杂度 $O(n + 2^{\lvert \Sigma \rvert})$。（$\lvert \Sigma \rvert = 22$ 不是 $26$ 就是为了防止在这里爆空间啦）

线段树合并

思想和静态链分治很相似，都是要对每个节点维护一个大 $info$。~~因此前面的好几个例题也都是线段树合并的例题。~~

我们的目标是合并两棵树：

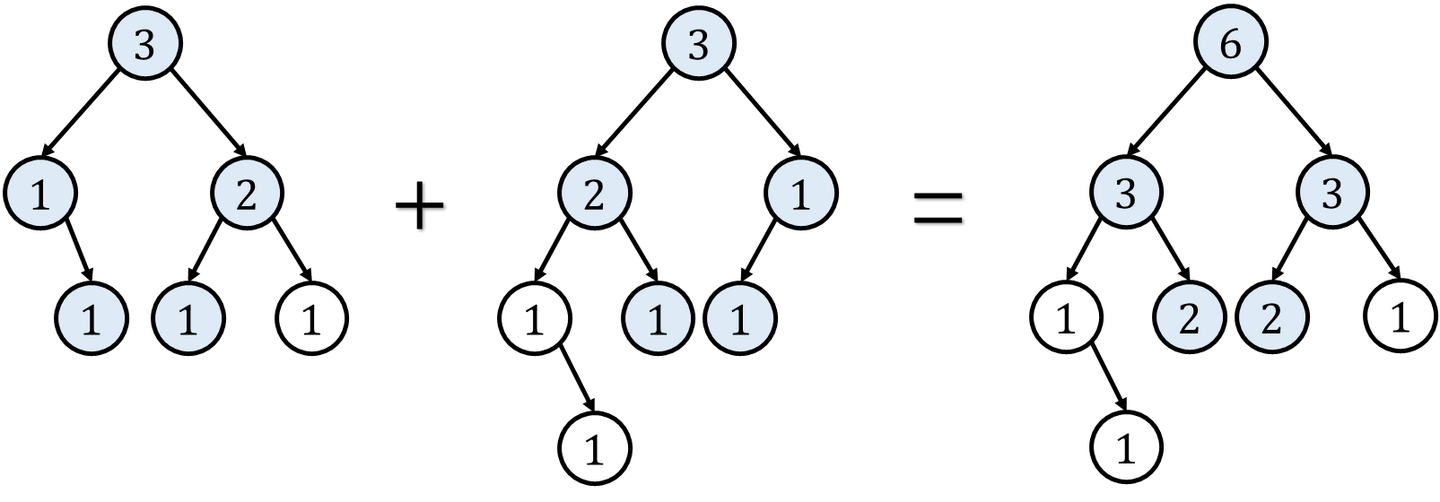
第一种实现方式类似于可持久化：

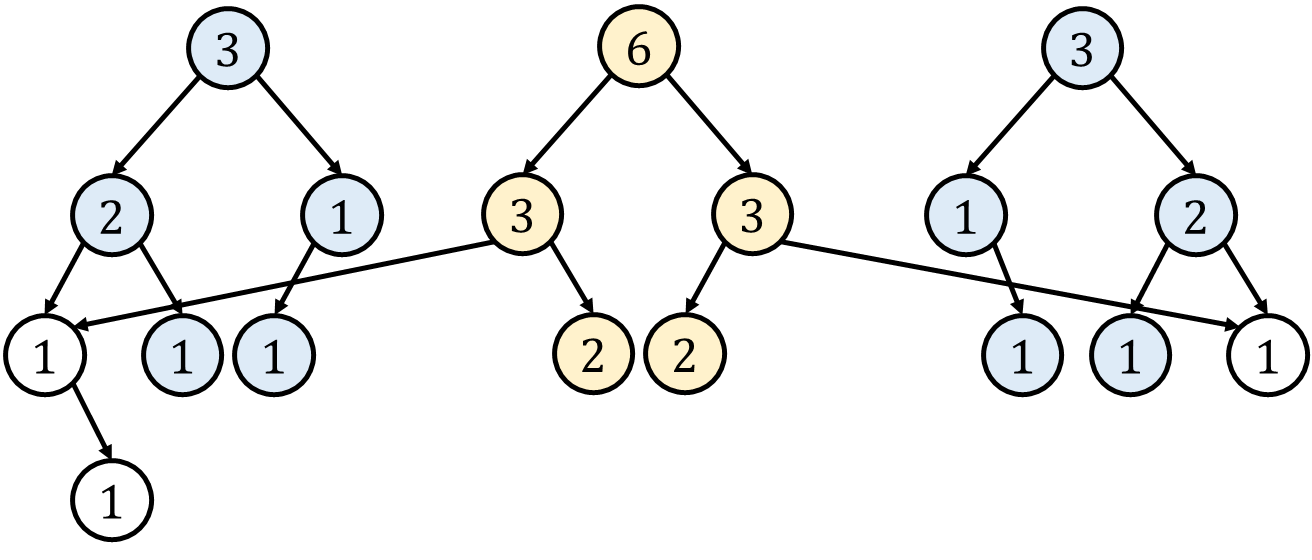
第二种方式更省空间，但是会丢失一棵树的信息：

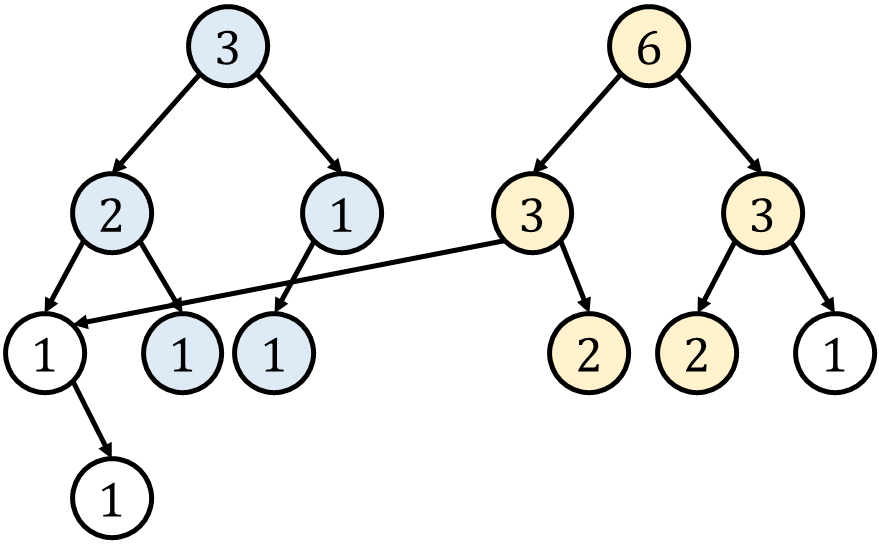
Alex_Wei 说涉及修改时，线段树合并很多时候和标记永久化一起用。

时间复杂度分析

令 $T_1 \odot T_2$ 表示线段树 $T_1,T_2$ 合并得到的线段树，$\lvert T \rvert$ 表示线段树 $T$ 的节点数量。

结论：对于 $n$ 棵线段树 $T_1, T_2, \cdots, T_n$，将它们以任意顺序合并得到树 $T_f$。总时间复杂度为 $O(\sum\limits_{i=1}^n \lvert T_i \rvert - \lvert T_f \rvert) = O(n \log V)$。

证明：考虑数学归纳。

假设命题对于 $n < N$ 都成立，我们要证明 $n = N$ 的情况。我们把这 $n$ 棵树分为两个不交的集合 $S_1, S_2$，分别以任意顺序合并得到线段树 $A_1, A_2$，然后合并这两棵树。

任意顺序合并出 $A_1, A_2$：$O(\sum\limits_{T \in S_1} \lvert T \rvert - \lvert A_1 \rvert) + O(\sum\limits_{T \in S_2} \lvert T \rvert - \lvert A_2 \rvert)$，即 $O(\sum\limits_{i=1}^n \lvert T_i \rvert - \lvert A_1 \rvert - \lvert A_2 \rvert)$。
合并 $A_1, A_2$：遍历到的不重叠节点数量不超过重叠节点的 $2$ 倍，因此复杂度和重叠节点数成正比，为 $O(\lvert A_1 \rvert + \lvert A_2 \rvert - \lvert A_1 \odot A_2 \rvert)$。

加起来得到整个过程的复杂度为：

\[O(\sum\limits_{i=1}^n \lvert T_i \rvert - \lvert T_f \rvert)\]

Ref

线段树合并例题

P3521 [POI 2011] ROT-Tree Rotations (Normal)

给一棵 $2n-1$ 个节点的二叉树，每个叶子上有一个 $[1,n]$ 的数字，保证每个数字出现且仅出现一次。现在允许任意次交换某两棵兄弟子树。对操作完毕的树进行 DFS，可以得到一个先序遍历序，它是一个 $[1,n]$ 的排列。求这个排列最小的逆序对数。
$n \le 2 \times 10^5$。

令 $u$ 是一个非叶子节点，$l,r$ 是它的两个儿子。令 $T_u$ 表示 $u$ 的子树，$f(u)$ 表示 $T_u$ 内的逆序对数。

\[f(u) = f(l) + f(r) + \sum \limits_{x \in T_l, y \in T_r} [x > y]\]

前两项直接递归，而且和这一层要不要交换毫无关系。看第三项。

如果我们能对每个节点维护一个桶，然后就可以每次用 $l,r$ 的桶统计答案。

显然时空会爆，但是这个思路是可行的。我们只要对叶子用平衡树（要支持查 rank 操作）维护桶，然后每次递归回来的时候启发式合并（因为 $l,r$ 的桶对后面的计算无用，直接合起来当 $u$ 的桶），时间复杂度 $O(n \log^2 n)$。写 Splay 应该能做到 $O(n \log n)$？

看一下比较稳的 1log 做法。我们改用线段树维护桶，然后线段树合并。

如果不交换，线段树每一处节点合并贡献是 $l$ 的线段树右子树和乘 $r$ 的线段树左子树和。若交换就是反一下。

时间复杂度 $O(n \log n)$。

长链剖分

P5904 [POI 2014] HOT-Hotels 加强版 (Hard)

TODO:

整体二分 & CDQ

$O((n+m) \log n)$ 离线静态区间 k 小值

点分治

序列分治的过程：每次取中点，计算穿过中点的区间答案，在中点两边分别递归。

树上点分治的过程：每次取重心，计算穿过重心的路径答案，以重心为根递归每棵子树。

为什么选择树的重心？树的重心有性质：以树的重心为根时，所有子树的大小都不超过整棵树大小的一半。每次递归子树大小至少减半，递归层数就是 $O(\log n)$ 的，每层 $O(n)$，总时间复杂度 $O(n \log n)$。

点分治例题

💡P4149 [IOI 2011] Race (Easy)

给一棵树，每条边有权。求一条简单路径，权值和等于 $k$，且边的数量最小。
$n \le 2 \times 10^5$，值域 $10^6$。

放一道入门题过来。这题是刚才静态链分治的例题。

这题有些太简单了，只要开一个 $10^6$ 的桶维护即可。

重点是放一下代码看细节：

int n, k;
vector<pair<int, int>> G[MAXN];

bool vis[MAXN]; // 是否已经成为过重心
int siz[MAXN] /*子树大小*/, mx[MAXN] /*最大儿子子树大小*/;
int centroid;
int tot; // 当前树的总点数
void get_centroid(int u, int fa) { // 找重心，储存在 centroid
    if (vis[u]) return;
    siz[u] = 1;
    mx[u] = 0;
    for (auto [v, w] : G[u]) if (v != fa && !vis[v]) {
        get_centroid(v, u);
        mx[u] = max(mx[u], siz[v]);
        siz[u] += siz[v];
    }
    mx[u] = max(mx[u], tot - siz[u]);
    if (!centroid || mx[u] < mx[centroid])
        centroid = u;
}
int ans = INF; // 最终答案
int pre[MAXM]; // 这棵子树之前的子树的总桶
vector<int> del; // 要清空的桶的位置
void calc(int u, int fa, int dep, int dis) { // 计算这棵子树和之前子树产生的贡献
    if (dis > k)
        return;
    cmin(ans, dep + pre[k - dis]);
    for (auto [v, w] : G[u]) if (v != fa && !vis[v]) {
        calc(v, u, dep+1, dis+w);
    }
}
void rec(int u, int fa, int dep, int dis) { // 把这棵子树的信息记录进总桶
    if (dis > k)
        return;
    cmin(pre[dis], dep), del.push_back(dis);
    siz[u] = 1;
    for (auto [v, w] : G[u]) if (v != fa && !vis[v]) {
        rec(v, u, dep+1, dis+w);
        siz[u] += siz[v];
    }
}
void solve(int u) { // 点分治
    get_centroid(u, 0);
    u = centroid, vis[u] = true, centroid = 0;
    pre[0] = 0;
    for (auto [v, w] : G[u]) if (!vis[v]) {
        calc(v, u, 1, w);
        rec(v, u, 1, w);
    }
    for (auto x : del)
        pre[x] = INF;
    del.clear();
    for (auto [v, w] : G[u]) if (!vis[v]) {
        tot = siz[v];
        solve(v);
    }
}

// main 里调用
    rep(x, 0, k)
        pre[x] = INF;
    tot = n;
    solve(1);

尤其注意清空的时候不能大手一挥用 memset 或者一个循环直接碾过去，时间复杂度 $O(nV)$ 当场死给你看。再递归一次一个一个清空，或者用一个容器装好所有要销毁的位置一起清空（代码用的是后者）。

颜色树 (Hard)

网上没有原题。

给定一棵 $n$ 个点的树，树上每个节点均有颜色。求有多少条路径包含了所有 $k$ 种颜色。
$k \le 10$。
需要一个低于 $O(2^k n \log n)$ 的做法。

先点分治。$k \le 10$ 显然是压位。问题转化为：

往集合 $S$ 插入一个二进制数
给定一个 $x$，求 $\sum\limits_{y \in S} [x \subseteq y]$。$x \subseteq y$ 代表 $x \land y = x$。

暴力做插入 $O(1)$ 查询 $O(2^k)$。考虑平衡。神秘小 Trick：

设 $f_{A,B}$ 表示有几个二进制数前一半为 $A$ 后一半包含 $B$（空间复杂度 $O(2^k)$）。

插入时 $A$ 确定，枚举 $B$，时间复杂度 $O(\sqrt{2}^k)$。
查询时 $B$ 确定，枚举 $A$，时间复杂度 $O(\sqrt{2}^k)$。

总时间复杂度 $O(\sqrt{2}^k n \log n)$。

这个 Trick 以前没有见过，有点意思。在二进制的相关问题提供了一个“分块”的思路。

Self-Driving Bus

给一棵树，结点编号为 $[1,n]$，求有多少个编号区间使得对应结点连通。
$n \le 10^5$。

考虑怎么刻画连通。树上 $x$ 个点连通当且仅当有 $x-1$ 条边把它们连起来。

TODO:

Ref: 网上仅有的两篇题解

[【题解】HackerRank - Self-Driving Bus Zerol’s Notes](https://zerol.me/2018/02/10/Self-Driving-Bus/)
[hackerrank]Self-Driving Bus - CSDN

P10632 Normal (Hard)

给定一棵 $n$ 个点的树，求每次均匀随机选择一个点当重心的点分治的期望时间复杂度（每次执行点分治的连通块的大小之和的期望）。保留四位小数。
$n \le 3 \times 10^4$。

设随机变量 $f_{u,v} \in {0,1}$ 表示在某次分治中以 $u$ 作为根节点，$v$ 是否在 $u$ 的连通块内，换句话说为 $v$ 对 $u$ 的贡献。令概率 $p_{u,v} = P(f_{u,v} = 1)$。

虽然事件之间不独立，但是根据期望的线性性，答案为：

\[\mathbb E\left[ \sum \sum f_{u,v} \right] = \sum \sum \mathbb E[f_{u,v}] = \sum \sum p_{u,v}\]

观察 $u \leftrightsquigarrow v$ 这条链，当且仅当 $u$ 是这条链上第一个被选中的点时，事件 $f_{u,v} = 1$ 才会发生。链上每一个点被首次选中的概率是相等的，因此概率为 $\frac 1 {\text{dis}(u, v) + 1}$。

这一步也可以看成，枚举 $v$，对 $u$ 做 CF280C Game on Tree。

最终答案即为树上所有链的点数倒数和：

\[\sum\limits_{u} \sum\limits_{v} \frac 1 {\text{dis}(u, v) + 1}\]

变个形，设 $c_i$ 为长度为 $i$ 的路径个数。

\[n + 2 \sum\limits_{i=1}^{n-1} \frac {c_i} {i + 1}\]

统计全局路径的问题，考虑点分治。

每一次分治时的 $c$ 数组可以 FFT 得到。

FFT 时有一个细节，要按子树大小排序之后依次 FFT（按照子树高度也可以），每次卷积时间复杂度 $O(siz_v \log siz_v)$，最终总时间复杂度 $O(n \log^2 n)$。

如果不排序，时间复杂度会退化到 $O(n^2 \log^2 n)$（不太确定能不能到 2log，但是 1log 肯定可以）。只看一层递归的话，卡法是开头放一个 $\frac n 2$ 的子树，后面放 $\frac n 2$ 个 $1$ 的子树。

总之，总时间复杂度 $O(n \log^2 n)$。

这个题目告诉我们，求出所有链长的值域数组是比较困难的，需要 2log 的点分治 + FFT，所以非必要不要把题目往这方面想；真遇到了这种题也只能认了，没有简单做法。

点分树

把点分治的每一次重心连成树，就得到了点分树。

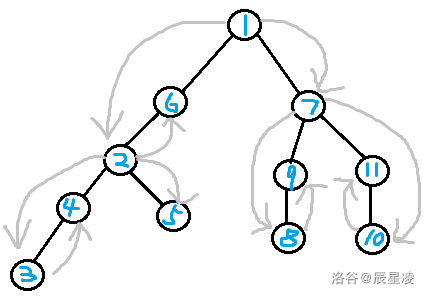
点分树树高 $O(\log n)$，显然 $\sum siz_u = O(n \log n)$。这两个式子是点分树的核心性质。

由于树高非常小，很多时候修改可以暴力跳父亲。

点分树不会保留原树的形态特点，对于路径问题或者连通块问题比较有好处。并不是一定要查到 $u,v$ 的 LCA 才能得到 $u \leftrightsquigarrow v$ 的信息，在路径上随便选一点就行了。事实上，我们利用点分树解决问题时，使用的就是 $u,v$ 在点分树上的 LCA。

接下来用一道经典老题展示一下点分树的处理手法。

给定一棵树，对于树上的所有节点 $u$，计算 $\sum\limits_{v=1}^n \text{dis}(u,v)$。
$n \le 10^5$。

这个题有简单的换根做法，但是我们考虑点分树，看看怎么利用树高为 $O(\log n)$ 的性质。

对于任意一个 $v$，我们可以找到点分树上的 LCA。根据点分树的定义，以 LCA 为重心时 $u,v$ 首次被分隔开。

对于每个 $u$，我们反过来枚举这个 LCA（总共只有 $O(\log n)$ 个），$v$ 就只会出现在 LCA 儿子的子树中，可以通过预处理信息得到。

注意不要把 $\text{deg}_{\text{LCA}}$ 带进时间复杂度，每一个 $\text{LCA}$ 处的统计应该是比较小的，$O(1)$ 或者 $O(\log n)$（当然这题是 $O(1)$，我们预处理全部儿子的信息总和，再减掉一个特定儿子）。

时间复杂度 $O(n \log n)$。~~全方面被换根吊打~~。

可持久化点分树

见下面例题 #6073. 「2017 山东一轮集训 Day5」距离。

点分树例题

P6329 【模板】点分树 | 震波 (Normal)

维护一颗带点权树，需要支持两种操作：
给定 $x$，修改 $x$ 的点权。
给定 $x,k$，查询与点 $x$ 距离不超过 $k$ 的点权值之和。
$n,m \le 10^5$。

不带修做法

模仿上一题的信息预处理，我们预处理 $f_{i,j}$ 代表点分树上 $i$ 的子树中与 $i$ 距离小于等于 $j$ 的点权之和，$g_{i,j}$ 代表点分树上 $i$ 的子树中与 $fa_i$ 距离小于等于 $j$ 的点权之和。

对于一个查询 $(x,k)$，对于 $x$ 祖先中的一对父子 $u \leftrightarrow fa_u$，令 $w = \text{dis}(x,fa_u)$，则贡献为 $F(u) = f_{fa_u, k-w} - g_{u, k-w}$，要判一下 $k-w$ 是否合法。注意 $\text{dis}$ 是原树距离。

最终答案为 $f_{x,k}$ 加上 $x$ 的所有祖先 $u$ 的 $F(u)$。

计算 $\text{dis}$ 需要 $\text{LCA}$，如果树剖求就是 $O(\log n)$，如果用 Alex_Wei 的 DFS 序就是 $O(1)$。

令 $n,m$ 同阶，总时间复杂度 $O(n \log^2 n)$ 或者 $O(n \log n)$。

完整做法

注意到单点修改在点分树上也只影响祖先的信息，我们依然可以暴力跳父亲。

每一个单点修改会带来对 $f_i$ 和 $g_i$ 的后缀修改，同时我们在查询时又要支持 $f_i$ 和 $g_i$ 的单点查询，我们使用树状数组来维护。

令 $n,m$ 同阶，总时间复杂度 $O(n \log^2 n)$。

注意空间复杂度：数组第二维 $j$ 表示距离，不会超过点分治当前连通块的大小，也就是说树状数组的上限只要开到 $siz_u$ 就行了。我们开树状数组时用 vector 精细地实现，空间复杂度就是 $O(\sum siz_u) = O(n \log n)$。

#6073. 「2017 山东一轮集训 Day5」距离

ZJY 的独家做法。

给定一棵 $n$ 个点的边带权树和一个排列 $p$。有 $q$ 个询问，给定节点 $l,r,k$，求：
\[\sum\limits_{j \in l \leftrightsquigarrow r} \text{dis}(p_j, k)\]
$n,q \le 2 \times 10^5$，值域 $10^9$，强制在线。

首先问题规约到

\[\sum\limits_{j \in \text{root} \leftrightsquigarrow x} \text{dis}(p_j, k)\]

每个询问都能用 $4$ 个这玩意儿拼出来。

我们固定 $x$ 看 $k$，发现可以点分树做。

给每个 $\text{root} \leftrightsquigarrow x$ 一个版本的点分树，我们发现把 $x$ 往远离 $\text{root}$ 方向移动一步，就会多加入一个 $p_j$，只会修改 $O(\log n)$ 个节点。我们可以把这 log 个节点 path copy 出来，做成类似可持久化线段树的结构。每次新版本是 $O(\log n)$ 的，每次查询也是 $O(\log n)$ 的，最终时间复杂度 $O(n \log n)$。

Share on

Bluesky Facebook LinkedIn X (formerly Twitter)

Xinyuan Mao

数据结构 5

静态链分治

CF600E Lomsat gelral

静态链分治例题

CF208E Blood Cousins (Easy)

P4149 [IOI 2011] Race (Easy)

CF741D Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths (Normal)

线段树合并

时间复杂度分析

Ref

线段树合并例题

P3521 [POI 2011] ROT-Tree Rotations (Normal)

长链剖分

CF1009F Dominant Indices

P5904 [POI 2014] HOT-Hotels 加强版 (Hard)

P5903 【模板】树上 K 级祖先

整体二分 & CDQ

P3332 [ZJOI2013] K大数查询

P4093 [HEOI2016/TJOI2016] 序列

P4095 [HEOI2013] Eden 的新背包问题

点分治

点分治例题

💡P4149 [IOI 2011] Race (Easy)

颜色树 (Hard)

Self-Driving Bus

P10632 Normal (Hard)

点分树

可持久化点分树

点分树例题

P6329 【模板】点分树 | 震波 (Normal)

不带修做法

完整做法

#6073. 「2017 山东一轮集训 Day5」距离

Share on

You May Also Enjoy

TestPost

Cycle Space 与 Cut Space

图论 1

函数的极值

Xinyuan Mao

静态链分治

静态链分治 例题

CF208E Blood Cousins (Easy)

P4149 [IOI 2011] Race (Easy)

CF741D Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths (Normal)

线段树合并

时间复杂度分析

Ref

线段树合并 例题

P3521 [POI 2011] ROT-Tree Rotations (Normal)

长链剖分

P5904 [POI 2014] HOT-Hotels 加强版 (Hard)

整体二分 & CDQ

点分治

点分治 例题

💡P4149 [IOI 2011] Race (Easy)

颜色树 (Hard)

P10632 Normal (Hard)

点分树

可持久化点分树

点分树 例题

P6329 【模板】点分树 | 震波 (Normal)

不带修做法

完整做法

Share on

You May Also Enjoy

静态链分治例题

线段树合并例题

点分治例题

点分树例题