根号算法：分块 & 块状链表 & 莫队

这一类问题的思路是：先思考小数据时怎么做，合并又怎么做。

分块很熟悉了，什么是块状链表？

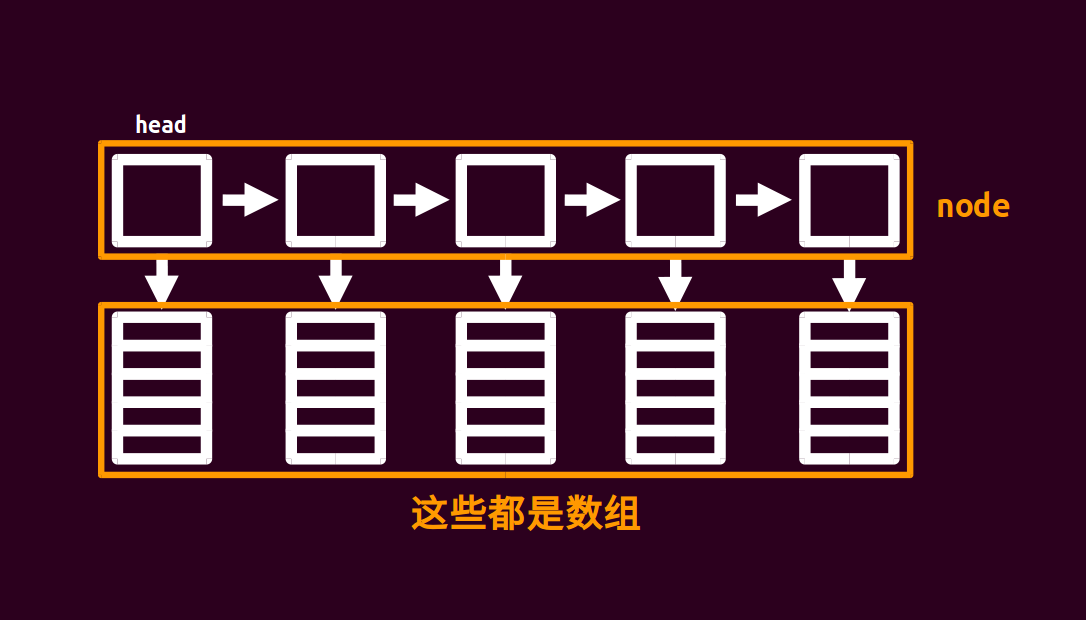
每日任务：从 OI-Wiki 偷图

显然这样的结构和分块是大差不差的，只要每个块的大小都是 $O(B)$ 级别（$B$ 是块长）。而且相比分块来说，它还能支持插入。

一个小问题是，如果我一直在同一块上插入的话，块的大小就不是 $O(B)$ 然后就退化了。所以一般的解决办法是：当块的大小达到 $2B$ 时，暴力分裂成两个块。

根号算法 例题

P3203 [HNOI2010] 弹飞绵羊 (Normal)

上面已经有 LCT 思路了，接下来介绍一个绝妙的分块思路。

这个思路真的超级离谱啊，为什么会有人在这种题目想到分块啊…… 或许正是因为要维护的东西过于离谱吧。

对每个点维护 $step_i$ 和 $to_i$，分别表示跳出当前所在块需要的步数，以及跳到的位置。

查询非常直接：

// 点的编号是 1~n 而非题目里的 0~(n-1)
int query(int x) {
    if (x > n)
        return 0;
    return query(to[x]) + step[x];
}

单点修改直接重构整个块即可。

查询 $O(\frac n B)$，单点修改 $O(B)$，平衡一下取 $B = \Theta(\sqrt n)$。总时间复杂度 $O(n \sqrt n)$。

P4278 带插入区间K小值 (Normal)

序列，插入，单点修改，查询区间 k 小值。强制在线。 操作数以及值域都在 $7 \times 10^4$ 以内。

首先带插入，所以想到平衡树和块状链表。平衡树又难写常数又大，所以我们想一下块状链表的思路。（注：本题确实有平衡树的 $\text{polylog}$ 做法）

联想到以前做过的 P2801 教主的魔法，在那题中我们实现了查询区间中 $\le k$ 的数的个数。

我们发现查询第 $k$ 小可以用二分答案以多一个 $\log V$ 的代价转化为上面的那个问题。然后就做完了。

时间复杂度分析。

认为 $n,q$ 同阶。

• 修改：$O(B)$（不重构时）
  • 有重构 $O(B \log B)$，重构总次数 $O(\frac n B)$，总复杂度 $O(n \log B)$，均摊下来 $O(\log B)$ 忽略。
• 查询：$O(B + \frac {n \log V} B \log B)$。

解得 $B = \Theta(\sqrt{n \log V (\log n + \log \log V)})$。若进一步认为 $n,V$ 同阶，则 $B = \Theta(\sqrt n \log n)$。实测开 $B = 512$ 能过，而且不卡常。

总结：$n,q,V$ 同阶的情况下，时间复杂度 $O(n \sqrt n \log n)$。

课后作业 3 - P2137 Gty的妹子树

一颗树，根节点为 $1$，要求支持在线添加一个结点、修改一个结点权值和询问子树内权值大于 $x$ 的点的个数。强制在线。 $n,q \le 3 \times 10^4$，值域 $2^{31}$。

块状链表维护 DFS 序，用 Splay 例题 Gty的游戏 的 Trick 支持查询子树，即多维护一个深度然后二分。TODO:

修改 $O(B)$；查询 $O(B + \frac {n \log n} B)$。解得 $B = \Theta(\sqrt{n \log n})$。

AT_joisc2014_c 歴史の研究【强制在线】(Hard)

类似题目：P4168 [Violet] 蒲公英

求区间加权众数（$x$ 乘上 $x$ 的出现次数 的最大值）。 $n,q \le 10^5$，值域 $10^9$。

令 $n,q$ 同阶。

众所周知这两个题离线的话就是回滚莫队的板子。但是现在被强制在线了，我们只能用分块了。

对于这一类高级分块问题，我们一般采取的思路是：预处理 $ans_{L,R}$ 表示第 $L$ 块到第 $R$ 块的答案，然后每次查询的时候扫描散块的剩余部分来计算影响。

这么说太抽象了，我们来看具体的思路：

首先起手一个离散化。设 $ans_{i,j}$ 表示第 $i$ 块到第 $j$ 块的加权众数，再设一个 $sum_{i,v}$ 表示前 $i$ 块中 $v$ 的出现次数，方便后面计算。

这两个数组都可以 $O(n \sqrt n)$ 预处理，这里讲一下 $ans$：$O(\sqrt n)$ 枚举 $i$，$O(\sqrt n)$ 枚举 $j$，再开一个 $O(\sqrt n)$ 大小的桶就行了。

询问 $[l,r]$ 时，我们先把答案预设为当中整块的答案 $ans_{i,j}$，然后扫描散块，看看散块中出现的加权众数有没有比 $ans_{i,j}$ 大，这里需要用到 $sum$ 数组。

总复杂度 $O(n \sqrt n)$。

BZOJ3744 Gty的妹子序列 | P5046 [Ynoi2019 模拟赛] Yuno loves sqrt technology I

hydro

查询静态区间逆序对。强制在线。 $n,m \le 5 \times 10^4$ | $n,m \le 10^5$。

TODO:

BZOJ3787 Gty的文艺妹子序列 (Hard)

hydro

支持单点修改的上面那题。强制在线。

TODO:

莫队 例题

BZOJ3809 Gty的二逼妹子序列 | P4867 Gty的妹子序列

给定一个序列 $a_{[1,n]}$，$m$ 次询问值域在 $[a,b]$ 内的数在区间 $[l,r]$ 中出现了多少种。 所有东西在 $10^5$ 内。

直接莫！修改次数 $O(n \sqrt n)$，询问次数 $O(n)$，权值线段树维护，总时间复杂度 $O(n \sqrt n \log n)$，寄！

我们发现修改和询问并不是平衡的，因此我们调大询问复杂度，改用值域分块，修改复杂度 $O(1)$，询问复杂度 $O(\sqrt n)$。总时间复杂度 $O(n \sqrt n)$，过！

P4074 [WC2013] 糖果公园

给定一棵树，每个点有一个颜色 $col_u$。 给定两个权值数组 $v$ 和 $w$。 两种操作：

• 修改一个点的颜色。
• 对于一条路径，询问 $\sum\limits_{c \in \text{colors}} v_c \sum\limits_{i=1}^{cnt_c} w_i$，其中 $cnt_c$ 表示路径上颜色 $c$ 出现的次数。

$n,q \le 10^5$，$v_i, w_i \le 10^6$。时限 $6$ 秒。

如果是序列问题的话，直接带修莫就做完了。$O(n^{\frac 5 3})$ 美滋滋。但是现在是树。

树上莫队

求出括号序，用 $fi_u$ 和 $la_u$ 表示一个节点 $u$ 两次出现在括号序中的位置。

假设求的是 $u \leftrightsquigarrow v$ 的信息。分类讨论：

• $u$ 和 $v$ 是子孙后代关系：$[fi_u, fi_v]$（大小关系可能要反一下）。
• 否则：$[la_u, fi_v]$（大小关系可能要反一下），并且要额外算上 $\text{LCA}(u, v)$，并且去掉出现了 $2$ 次的节点。

然后和以前一样莫就可以了！依然是 $O(n^{\frac 5 3})$。