字符串 1
Published:
全文的 index 都从 $1$ 开始。
DFA
DFA 是 deterministic finite automaton 的缩写，即确定有限状态自动机。
- 基本概念：https://oi-wiki.org/string/automaton/
- 自动机五要素：
- 字符集 $\Sigma$。
- 状态集合 $Q$。
- 起始状态 $start$。
- 接收状态集合 $F$。
- 转移函数 $\delta$。$\delta(u,c)$ 中 $u,\delta(u,c) \in Q$，$c \in \Sigma$。
MP
首先澄清一个误区：大家平时说的 KMP 其实指的都是 MP 算法（Morris-Pratt 算法）。在后面的题中我们就能看到完全体的 KMP 算法（Knuth-Morris-Pratt）的用处。
在除了这一段以外的部分，无特殊说明时 KMP 指 MP 算法。
给你两个字符串 $S$ 和 $T$，问 $S$ 在 $T$ 中出现的所有位置。
令 $n = \lvert S \rvert$，$m = \lvert T \rvert$。 需要 $O(n + m)$ 的做法。
我们尝试对 $S$ 搭建一个 DFA，使它仅接受以 $S$ 为后缀的字符串。然后我们输入 $T$ 看看 $T$ 的哪些前缀被接受即可。考虑如何搭建这个 DFA。
观察暴力匹配的过程，我们发现有很多时候都是因为我们重复查看了某些信息导致冗余。（观看视频《最浅显易懂的 KMP 算法讲解》的 1:38-4:20 获得更直观的理解）根据这样的直觉，我们可以构建出以下 DFA。
\[\delta(u,c) = \begin{cases} u+1 & c = S_{u+1} \\ 0 & c \ne S_{u+1} \land u = 0 \\ \delta(next(u),c) & c \ne S_{u+1} \land u \ne 0 \end{cases}\]（特别地，$S_{n+1} \not \in \Sigma$，即走到 $u=n$ 的时候一定走第三个转移）
$next(u)$ 代表 $S_{[1,u]}$ 的最大 border 长度（对应在 DFA 上的状态），也记作 $\pi_u$。可以这样求得：
\[next(u) = \begin{cases} 0 & u = 1 \\ \delta(next(u-1), S_u) & u \ne 1 \\ \end{cases}\]完整建出 $\delta$ 时间复杂度 $O(n \lvert \Sigma \rvert)$。
但是如果只是求 $next$ 数组的话，其实有更优秀的做法。暴力模拟这个递归，总时间复杂度就是 $O(n)$ 的。
nxt[1] = 0;
rep(i, 2, n) {
int p = nxt[i-1];
while (p && S[p+1] != S[i])
p = nxt[p];
if (S[p + 1] == S[i])
p++;
nxt[i] = p;
}
接下来证明时间复杂度。首先把代码写成另一种等价的形式：
nxt[1] = 0;
int p = 0;
rep(i, 2, n) {
// p 直接继承上一个 nxt
while (p && S[p+1] != S[i])
p = nxt[p];
if (S[p+1] == S[i])
p++;
nxt[i] = p;
}
不难发现 $p$ 自增的次数是 $O(n)$ 的，而 $p$ 非负，因此 $p$ 减小的次数也是 $O(n)$ 的，证毕。本质上这是一个势能分析，也因此 MP 算法的复杂度是均摊的。
有了这个方法后，字符串匹配就很简单了：只要求出 $S + \text{#} + T$ 的 $next$（$\text{#} \not \in \Sigma$），找到所有 $next$ 为 $n$ 的地方即可。
当然还有一种更简单的写法，就是直接对着 $T$ 套用上面的第二个代码：
p = 0;
rep(i, 1, m) {
while (p && S[p+1] != T[i])
p = nxt[p];
if (S[p+1] == T[i])
p++;
if (p == n) {
cout << i-n+1 << '\n';
p = nxt[p]; // 成功匹配后要转移
}
}
像呼吸一样自然。
💡失配树
对于任意 $u$ 有 $next(u) < u$，因此形成一个树结构，称为失配树。
KMP
其实 MP 还能有小优化。
观察这个例子：算 ababab 的 $next$。
- 算到第 $3$ 个位置的
a时，正常来说 $next(3) = 1$。但是只要 $4$ 这个位置配不上，从 $3$ 落到 $1$ 之后也是配不上的，因为 $2$ 和 $4$ 的字符相同。所以完全没有必要落到 $1$，落到 $next(1) = 0$ 是更好的选择，因此直接把 $next(3) \gets 0$。 - 同理，算到 $5$ 时也没有必要落到 $next(5) = 3$，而是直接落到 $next(3) = 0$，因此 $next(5) \gets 0$。
总结：$S_{u+1} = S_{next_{\text{MP}}(u) + 1}$ 时，$next_{\text{KMP}}(u) \gets next_{\text{KMP}}(next_{\text{MP}}(u))$，否则 $next_{\text{KMP}}(u) \gets next_{\text{MP}}(u)$。
别忘了 $u+1$ 可能越界，特别判一下。
int nxt[MAXN];
void build() {
nxt[1] = 0;
int p = 0;
rep(i, 2, n) {
while (p && S[p+1] != S[i])
p = nxt[p];
if (S[p+1] == S[i])
p++;
if (i+1 <= n && S[p+1] == S[i+1]) // Here
nxt[i] = nxt[p]; // Here
else
nxt[i] = p;
}
}
注意 $next_{\text{KMP}}$ 相比于 $next_{\text{MP}}$ 丢失了 “前缀最长 border” 这个语义，性质相对没有那么好。
可持久化 (K)MP
超冷门科技。
这道例题没有地方提供评测。但是除此以外，有一道可以评测的类似题目：CF1721E Prefix Function Queries
[BZOJ NOI 十连测第 5 场 B] 可持久化字符串
一次操作会在字符串尾部添加一个字符，并且你需要在每次操作后输出最小 period 长度。 要求可持久化与在线。
$n \le 3 \times 10^5$，$\lvert \Sigma \rvert = O(n)$。
首先有结论（见下文 Border 与 Period 理论）：最小 period 长度为 $n - \pi_n$。也就是这个题肯定需要一个 KMP 家族的算法。
但是普通的 (K)MP 算法是无法支持可持久化的，因为复杂度是均摊的。
如果 $\lvert \Sigma \rvert$ 很小的话，直接建出 MP 自动机就行了，可惜是 $O(n)$。
TODO: 还在写
在 KMP 跳的时候同时维护 MP，用于求最小周期
倍增 $O(n \log^2 n)$。
参考：
AC 自动机
AC 自动机（Aho—Corasick automaton）接受且仅接受以指定的字符串集合 $S$ 中的某个元素 $S_i$ 为后缀的字符串。
即 MP 自动机的扩展版本。
我们把这个字符串集合塞进 Trie，然后在 Trie 上做 MP：
\[\delta(u,c) = \begin{cases} tr_{u,c} & tr_{u,c} \text{ exists} \\ 0 & tr_{u,c} \text{ does not exist} \land u = 0 \\ \delta(fail(u),c) & tr_{u,c} \text{ does not exist} \land u \ne 0 \end{cases}\]（$tr$ 表示这棵 Trie）
$fail(u)$ 为 $u$ 表示的字符串的出现在 Trie 上的最长真后缀对应的状态。
\[fail(u) = \begin{cases} 0 & u = 0 \\ \delta(fail(fa_u), c_u) & u \ne 0 \\ \end{cases}\]$c_u$ 表示 $u$ 的最后一个字符，即 $fa_u \to u$ 的这条边。
因为两者计算耦合，我们需要按深度求解，即 BFS 这棵 Trie。
void bfs() {
queue<int> q;
for (int c = 0; c < SIGMA; c++)
if (tr[0][c])
q.push(tr[0][c]);
while (!q.empty()) {
int u = q.front(); q.pop();
for (int c = 0; c < SIGMA; c++)
if (tr[u][c]) {
fail[tr[u][c]] = tr[fail[u]][c];
q.push(tr[u][c]);
} else
tr[u][c] = tr[fail[u]][c];
}
}
时间复杂度 $O(n \lvert \Sigma \rvert)$，其中 $n = \sum \lvert S_i \rvert$。
与 MP 的失配树同理，$fail$ 数组也形成一棵树，称为 fail 树。
Z 函数（扩展 KMP）
一个字符串的 Z 函数定义为它的每个后缀和它本身的 LCP 长度。即 $z_i = \text{lcp}(S, S_{[i,n]})$。
给定字符串 $S$ 和 $T$，求 $S$ 的 Z 函数，并求出 $T$ 和 $S$ 的每一个后缀的 LCP 长度数组 $p$。
对于 $i$，称区间 $[i, i + z_i - 1]$ 是 $i$ 的 Z-box。我们在算法运行过程中维护目前发现的右端点最大的 Z-box $[l,r]$。
现在我们要求 $z_i$，并且尝试利用 $i-1$ 及之前信息求得的 $[l,r]$。
- 如果 $i > r$，那么 $[l,r]$ 并不能帮上忙，暴力计算。
- 如果 $i \le r$：
- 分析：因为 $[l,r]$ 是一个 Z-box，所以 $S_{[1,r-l]} = S_{[l,r]}$。截取出同一段后缀：$S_{[i-l,r-l]} = S_{[i,r]}$，这段后缀的长度是 $len = r-i+1$。
- 如果 $z_{i-1} < len$，那么 $z_i = z_{i-l}$。
- 否则，$z_i$ 至少是 $len$，对于后面的部分 $[l,r]$ 又帮不上忙了，暴力计算。
- 如果新的 Z-box $[i, i + z_i - 1]$ 的右端点比 $r$ 大，那么要更新 $[l,r]$。
z[1] = n;
int l = 0, r = 0;
rep(i, 2, n) {
if (i <= r)
z[i] = min(z[i-l+1], r-i+1);
while (i + z[i] <= n && S[i + z[i]] == S[z[i] + 1])
z[i]++;
if (i + z[i] - 1 > r)
r = i + z[i] - 1, l = i;
}
记住 $i + z_i$ 可能越界，要判一下。
时间复杂度 $O(n)$，证明：每次暴力计算都会造成 $r$ 的自增（因为都是在 $[l,r]$ 帮不上忙的时候才算的），而 $r \le n$，暴力计算次数 $O(n)$，证毕。
第二问和 (K)MP 一样，构造 $T + \text{#} + S$ 这样的结构就迎刃而解。当然也可以直接把代码套上 $T$：
l = 0, r = 0;
rep(i, 1, m) {
if (i <= r)
p[i] = min(z[i-l+1], r-i+1);
while (i + p[i] <= m && T[i + p[i]] == S[p[i] + 1])
p[i]++;
if (i + p[i] - 1 > r)
r = i + p[i] - 1, l = i;
}
Manacher
给定一个长为 $n$ 的字符串，求出所有回文子串。注意到个数是 $O(n^2)$ 的，所以用一种更紧凑的形式表达：
在每个字符之间插入特殊字符，比如
aba变成#a#b#a#。接下来对于每个字符，求出以它为回文中心的最长回文串半径 $r_i$。比如以b为中心则半径为 $3$（#a#）。要求时间复杂度 $O(n)$。
模仿 Z 函数的思路。
（这一部分有字母冲突，注意区分 $r_i$ 和 $r$ 的不同含义）
对于 $i$，我们称 $[i, i+r_i]$ 是一个 box。我们在算法运行过程中维护目前发现的右端点最大的 box $[mid, r]$。
现在我们要求 $r_i$，并且尝试利用 $i-1$ 及之前信息求得的 box $[mid,r]$。
- 如果 $i > r$，那么 $[mid,r]$ 并不能帮上忙，暴力计算。
- 如果 $i \le r$：
- 分析：因为 $[mid, r]$ 是一个 box，所以令 $j = 2 \times mid - i$ 为 $i$ 关于 $mid$ 的对称点，以 $j$ 为中心 $r_j$ 为半径的回文串中，位于以 $mid$ 为重心 $r$ 为半径的回文串的部分就能映射到 $i$ 这里。
- 如果 $r_j < r-i$，那么 $r_i = r_j$。
- 否则，$r_i$ 至少是 $r-i$，对于后面的部分 $[mid,r]$ 又帮不上忙了，暴力计算。
- 如果新的 box $[i,i+r_i]$ 的右端点比 $r$ 大，那么要更新 $[mid,r]$。
（几乎就是照抄 Z 函数的思路了吧……每一步都有对应）
// MAXN 要开 2 倍！
int mid = 0, mx = 0; // [mid, mx] 维护的 box
rep(i, 1, n) {
if (i <= mx)
r[i] = min(r[2 * mid - i], mx - i);
while (i - r[i] >= 1 && i + r[i] <= n && S[i - r[i]] == S[i + r[i]])
r[i]++;
if (i + r[i] > mx)
mid = i, mx = i + r[i];
}
和 Z 函数一样，暴力扩展要记得判越界。
Border 与 Period 理论
- Border 与 period 一一对应：对于任意一个 border $k$，$n - k$ 必定为一个 period。
- 推论：最小 period 等于 $n - \pi_n$。P4391
- 弱周期引理 Weak Periodicity Lemma (WPL)：$p$ 和 $q$ 是 $S$ 的 period 且 $p + q \le \lvert S \rvert$，则 $\gcd(p, q)$ 也是 $S$ 的 period。
- 周期引理 Periodicity Lemma (PL)：$p$ 和 $q$ 是 $S$ 的 period 且 $p + q - \gcd(p, q) \le \lvert S \rvert$，则 $\gcd(p, q)$ 也是 $S$ 的 period。
- PL 严格强于 WPL。
- $p + q - \gcd(p,q)$ 这个下界是紧的，$\lvert S \rvert$ 再小就有反例了。
例题
P3893 [GDOI2014] Beyond (Normal)
给定两个长度为 $n$ 的字符串 $A$ 与 $B$，求出最大的 $L$，使得 $A$ 与 $B$ 的前 $L$ 个字符所组成的字符串循环同构。
需要低于 $O(n \log n)$ 的做法。
首先刻画循环同构这个条件：存在至少一种方案，把字符串分两块调换一下之后相同。
比如 $\texttt{abcd}$ 和 $\texttt{cdab}$ 就是 $\texttt{ab}$ 和 $\texttt{cd}$ 换一下的结果。
我们令 $s = \texttt{ab}$ 和 $t = \texttt{cd}$。
接着沿用这个例子，$s$ 在 $A$ 位于前缀，$B$ 中是一个普通的子串。注意子串是后缀的前缀，所以它是 $B$ 的某个后缀和 $A$ 的 LCP。Z 函数出现了。
同理，$t$ 是 $A$ 的某个后缀和 $B$ 的 LCP。
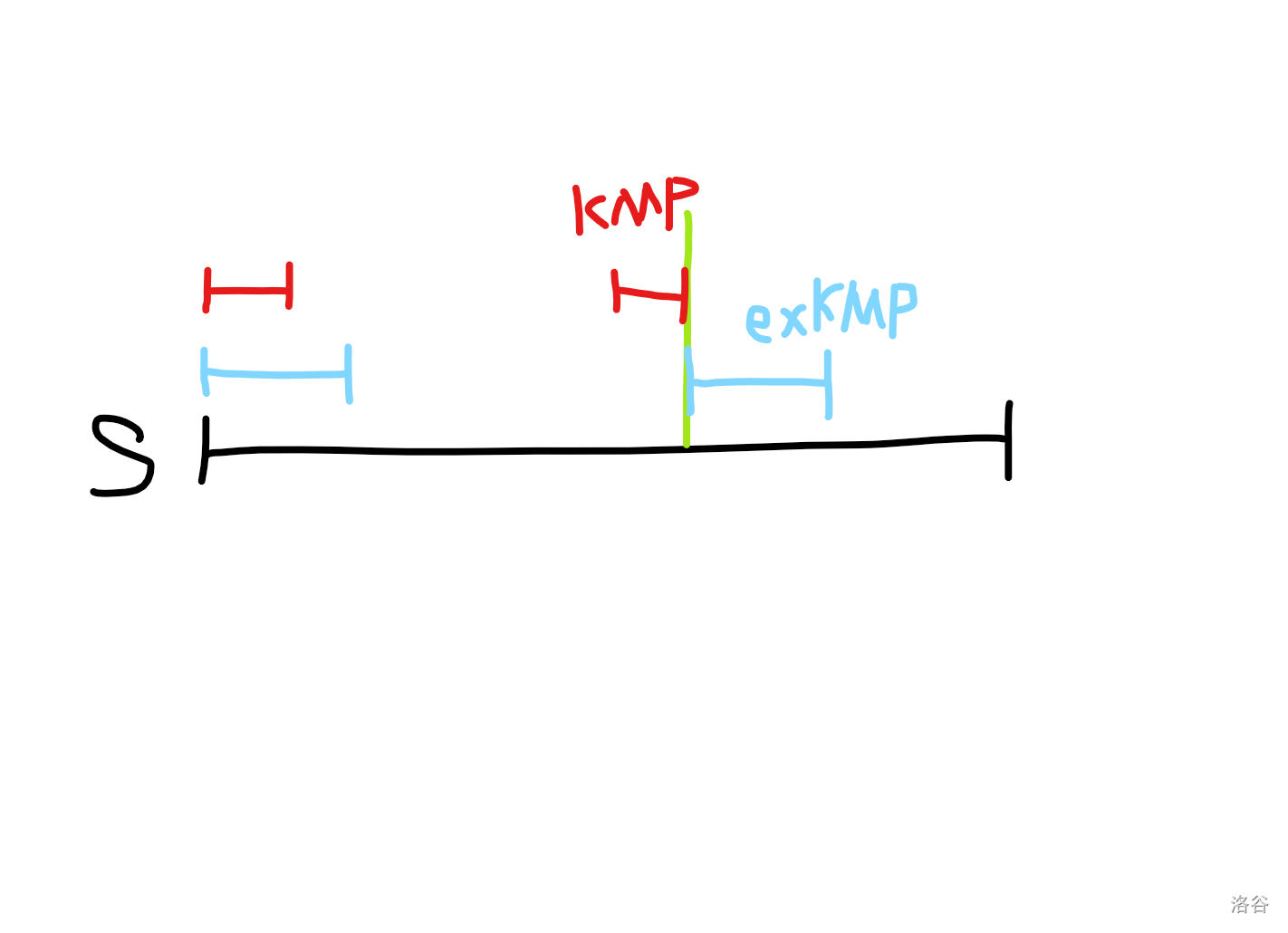
建出 Z 函数：
- $exA$ 表示 $A$ 的某个后缀和 $B$ 的 LCP。
- $exB$ 表示 $B$ 的某个后缀和 $A$ 的 LCP。
我们枚举 $A$ 的前缀 $A_{[1,i]}$ 作为 $s$。现在我们要求一个最大的 $j$，使得 $j \le exA_{i+1}$ 且 $exB_{j+1} \ge i$。答案即为 $\max i+j$。
这是一个二维偏序，可以使用树状数组 $O(n \log n)$。在原题上已经可以过了，但是其实不够优秀。
思考一下二维偏序的具体求解过程：我们把 $j$ 按 $exB_{j+1}$ 排序，倒序加入树状数组，在树状数组上查询 $[0,exA_{i+1}]$ 这个前缀的最大值。
这里我们用倒序是因为树状数组只支持加入而不能删除，但是我们其实还有一个只支持删除不支持插入的结构：序列并查集。
路径压缩与启发式合并都上，时间复杂度 $O(n \alpha(n))$。注意不要让排序称为瓶颈，用桶排序。
序列并查集练习题
P3715 [BJOI2017] 魔法咒语 (Easy)
用 $n$ 个字符串 $S$ 拼成一个长为 $L$ 的长串，长串中不能出现另外的 $m$ 个字符串 $T$，求总方案数。
- $n,m \le 50$
- $\sum \lvert S_i \rvert, \sum \lvert T_i \rvert \le 100$
- $\lvert \Sigma \rvert = 26$
这个题目有两个 Task：
- Task 1: $L \le 100$
- Task 2: $L \le 10^8$ 且 $\forall i$ 有 $\lvert S_i \rvert \le 2$。
对 $T$ 建 AC 自动机显然是没有问题的。为了避免禁忌词汇，拆除相应的 $\delta$ 即可。
注意到我们要恰好拼出 $L$，这很背包。设一个 01 背包：
令 $f_{u,i}$ 表示当前在 AC 自动机的节点 $u$，拼出串长为 $i$ 的方案数。
设 $to_{u,j}$ 表示 $u$ 后面输入 $S_j$ 到达的节点。
\[f_{u,i} = \sum\limits_{j=1}^n \sum\limits_{v} [to_{v,j} = u] f_{v,i-\lvert S_j \rvert}\]顺推（可以把 DP 柿子的两重循环都摊掉），时间复杂度 $O((n L + \lvert \Sigma \rvert) \sum \lvert T_i \rvert)$。
Task 2 即为对 Task 1 做法做矩阵快速幂，时间复杂度 $O((n + \lvert \Sigma \rvert) \sum \lvert T_i \rvert + (\sum \lvert T_i \rvert)^3 \log L)$。
P4324 [JSOI2016] 扭动的回文串 (Normal)
给定两个长度为 $n$ 的字符串 $A$ 和 $B$。 扭动的回文串定义为 $A_{[i,j]}$ 与 $B_{[j,k]}$ 相接成的字符串为回文串或者 $A$、$B$ 的一个回文子串。 求最长的扭动回文串。
需要一个 $O(n)$ 的算法。
$O(n \log n)$ 做法
枚举每一个回文中心。不妨设回文中心 $x$ 处于 $A$ 中（在 $B$ 中做法一样）。注意到必定从 $A$ 中的 $r_x$ 开始扩展是最优的，接下来一侧在 $A$ 中一侧在 $B$ 中，并且答案具有可二分性，二分哈希就做完了。
$O(n)$ 做法
思路来源：题解：P4324 [JSOI2016] 扭动的回文串 - wuxigk
注意到答案是 $O(n)$ 的，我们弄点势能的东西。每次从上次答案的基础上一个一个往外扩展（用哈希判定能否扩展），因为答案是 $O(n)$ 的所以只会扩展 $O(n)$ 次。
86ms，跑到最优解了可还行。
[ARC077F] SS (Hard)
定义：偶串是形如 $A+A$ 的串。 对于一个偶串 $S+S$，$f(S+S)$ 是满足以下条件的字符串：
- $f(S+S)$ 是偶串
- $S+S$ 是 $f(S+S)$ 的前缀
- $\lvert S+S \rvert < \lvert f(S+S) \rvert$。
省流版解释：$f(S+S)$ 是在 $S+S$ 后面添加一些字符得到的最短偶串。
给定字符串 $S$，求 $f^{\infty}(S+S)$ 的区间 $[l,r]$ 中每个字母的出现次数。$f^{\infty}$ 表示 $f$ 无穷多次复合。
$n = \lvert S \rvert \le 10^5$，$l,r \le 10^{18}$，$\lvert \Sigma \rvert = 26$。
令 $f(S+S) = T+T$ 和 $g(S) = T$，即 $f(S + S) = g(S) \times 2$。
$f^k(S+S) = g(f^{k-1}(S+S)) \times 2$，递归边界 $f^0(S+S) = S$，因此 $f^\infty(S+S) = g^{\infty}(S)$。
考虑求出 $g(S)$ 具体的形式：
首先 $T$ 一定是 $S+B$ 这样的形式。现在我们需要 $S+S$ 是 $T+T = S+B+S+B$ 的前缀，即 $S$ 是 $B+S$ 的前缀。
而 $S$ 又是 $B+S$ 的后缀，因此 $S$ 是 $B+S$ 的 border，根据 period 和 border 一一对应，$B$ 是 $B+S$ 的 period，即 $S$ 的 period。$B$ 又要最小，所以 $B$ 是 $S$ 的最小 period。
总结：令 $S$ 的最小 period 对应的串为 $A$，则 $T = g(S) = S + A$。
接着手玩容易猜出结论：
- 若 $\lvert A \rvert$ 是 $S$ 的整 period，则 $g^{\infty}(S)$ 就是 $A \times \infty$，非常好做。
- 否则，$\lvert S \rvert$ 必为 $S+A$ 的最小 period，即 $g^2(S) = (S+A) + S$。
递推：若定义 $g^{-1}(S) = A$ 和 $g^0(S) = S$，则
- $g^1(S) = g^0(S) + g^{-1}(S)$。
- $g^2(S) = g^1(S) + g^0(S)$。
$\lvert g^{k-2}(S) \rvert$ 一直是 $g^{k-1}(S)$ 的最小 period，一直是一个 $g(S) = S + A$ 的 pattern，所以 $g^k(S) = g^{k-1}(S) + g^{k-2}(S)$。
这就很 Fibonacci 了，所以 $\lvert g^k(S) \rvert$ 在 $k$ 增长时是指数级别增长的。这就很 $\log$。
时间复杂度 $O(n + \lvert \Sigma \rvert \log r)$。
对上述结论的证明
结论：令 $A$ 为 $S$ 的最小 period 对应的串，且 $\lvert A \rvert$ 不是 $S$ 的整 period。则 $S + A$ 的最小 period 对应的串为 $S$。
令 $T = S+A$。
首先 $\lvert S \rvert$ 显然是 $S+A$ 的一个 period。接下来尝试证明最小，考虑反证法，假设 $p$ 是 $S+A$ 的一个更短的 period，即 $p < \lvert S \rvert$。
首先 $p$ 也是 $S$ 的 period，而且 $\lvert A \rvert \le p$，因为 $A$ 是最小的。
我们有了两个 $S$ 的 period，尝试通过 (W)PL 构造一个更小的 period $\gcd(\lvert A \rvert, p)$，破坏 $\lvert A \rvert$ 的最小性以完成反证。那么接下来的证明分为两步：
- $\lvert A \rvert + p$ 的大小符合 (W)PL 的前置条件。
- $\gcd(\lvert A \rvert, p) < \lvert A \rvert$，确实是一个更小的 period。
在此处整理一下目前的所有条件：
- $\lvert A \rvert$ 是 $S$ 的最小 period，而且不是整的。
- $p$ 是 $T$ 的 period，推出 $p$ 是 $S$ 的 period，而且有 $\lvert A \rvert \le p < \lvert S \rvert$。
- 别忘了 $\lvert S \rvert$ 也是 $T$ 的 period。
步骤一
对于 $i \in [\lvert S \rvert + 1, \lvert T \rvert]$，$T_i = T_{i - \lvert S \rvert}$，因为 $\lvert S \rvert$ 是 $T$ 的 period。
使用 $p$ 是 $T$ 的 period，$T_i = T_{i-p}$，注意因为 $p \ge \lvert A \rvert$ 所以 $T_{i-p}$ 是落在 $S$ 范围内的。
联立两个式子得到 $T_{i - \lvert S \rvert} = T_{i-p}$ 对任意 $i \in [\lvert S \rvert + 1, \lvert T \rvert]$ 成立。平移一下可知 $\lvert S \rvert - p$ 是 $A$ 的 period。
使用 $\lvert A \rvert$ 是 $S$ 最小 period，得 $p \equiv \lvert S \rvert \pmod {\lvert A \rvert}$. TODO: 这步没懂，应该可以证明 $(\lvert S \rvert - p) \bmod \lvert A \rvert$ 是一个更小的 $S$ 的周期导出矛盾。
而 $p < \lvert S \rvert$，因此至少要差一整个 $\lvert A \rvert$，$p \le \lvert S \rvert - \lvert A \rvert$。
变形得 $\lvert A \rvert + p \le \lvert S \rvert$，符合 WPL 条件。
步骤二
依然反证。如果不满足 $\gcd(\lvert A \rvert, p) < \lvert A \rvert$ 的话，只能 $\gcd(\lvert A \rvert, p) = \lvert A \rvert$，即 $\lvert A \rvert \mid p$。
别忘了前面的同余关系 $p \equiv \lvert S \rvert \pmod {\lvert A \rvert}$，使用 $\lvert A \rvert \nmid \lvert S \rvert$ 的条件，可知 $\lvert A \rvert \nmid p$，矛盾。
考试的时候怎么测试此类结论？
- 枚举所有长度超级小的字符串。
- 对于大串，随机一个 $S$，然后用一些 $SSSSASS$ 这样的结构，其中 $A \ne S$。