字符串 2
Published:
SA
把一个字符串的后缀按字典序排序。按排名输出后缀位置。
题目要求的东西记为 $sa$ 数组,其反函数为 $rk$ 数组。
例如:eaabd,其后缀为 eaabd aabd abd bd d,排序后为 aabd abd bd d eaabd,$sa = \langle 2,3,4,5,1 \rangle, rk = \langle 5,1,2,3,4 \rangle$。
二分哈希直接排序当然也是 $O(n \log^2 n)$ 的,但是我们有更靠谱的做法。
以下内容来源:我自己的 SA 学习笔记。
求解考虑倍增。
初始轮,$w=1$,把 $sa$ 按每个后缀开头的字符排序。
接下来的每一轮,$w \leftarrow w \times 2$,这次的串 $x$ 应该由上一轮的 $[x,x+w)$ 和 $[x+w,x+2w)$ 两个后缀的前缀拼成。把 $sa$ 以 $rk_x$ 为第一关键字,$rk_{x+w}$ 为第二关键字排序,其中 $rk$ 为由上一轮的排序的 $sa$ 得到的 $rk$。
时间复杂度 $O(n \log^2 n)$,如果用基数排序可以做到 $O(n \log n)$。
int sa[MAXN], rk[MAXN * 2], tmp[MAXN * 2];
// 因为有 +w,开大一倍防止越界
// 因为在统计这一轮的 rk 时还要用到上一轮的 rk,所以这一轮的 rk 先放在 tmp 里,结束后 copy
void build_SA(string S) {
rep(i, 1, n)
sa[i] = i, rk[i] = S[i];
for (int w = 1; w <= n; w <<= 1) {
auto cmp = [&](int x, int y) -> bool {
if (rk[x] == rk[y])
return rk[x+w] < rk[y+w];
return rk[x] < rk[y];
};
sort(sa+1, sa+n+1, cmp);
rep(i, 1, n)
tmp[sa[i]] = tmp[sa[i-1]] + cmp(sa[i-1], sa[i]);
copy(tmp+1, tmp+n+1, rk+1);
}
}
Height 数组
定义:$h_i = \text{lcp}(sa_i, sa_{i-1})$。特别地,$h_1 = 0$。
Lemma $h[rk_i] \ge h[rk_{i-1}] - 1$。证明略。
基于这个引理,我们按 $rk$ 顺序暴力求出 $h$,均摊后总复杂度就是 $O(n)$。
int k = 0;
rep(i, 1, n) {
int j = sa[rk[i] - 1];
if (k) k--;
while (S[i + k] == S[j + k])
k++;
h[rk[i]] = k;
}
P2408 不同子串个数
求字符串 $S$ 的本质不同子串数量。
$\lvert S \rvert = n \le 10^5$。
按照 $sa$ 的顺序依次求解。$sa_{i-1}$ 和 $sa_i$ 的重复前缀数量为 $h_i$。
因此,答案为
\[\frac {n (n+1)} 2 - \sum\limits_{i=2}^n h_i\]记得开 long long。
SAM
提供一个 SAM 可视化网址:SAM Drawer
搭建一个自动机,接受且仅接受 $S$ 的所有后缀,且节点数最少。这个自动机称为后缀自动机(SAM),还有一个名字叫 Directed Acyclic Word Graph (DAWG)。
可以证明,节点数是 $O(n)$ 的。
1984 最新最热算法!
首先有一个小结论:把 SAM 上的所有节点都算成接受节点,SAM 就会变成“子串自动机”,接受且仅接受原串的子串。很简单,每个后缀都是从空串所在的节点一步一步转移过来的,所以肯定能经过每个后缀的前缀。后缀的前缀就是子串。
也就是说,SAM 其实是所有子串而不仅仅是所有后缀的集合体。
我们有一个 insight:一个子串会在原串中出现许多次(比如 $\texttt{aba}$ 在 $\texttt{abaababa}$ 的三个位置),这个子串的后缀也必然在这些位置出现,而且可能在更多位置出现(比如 $\texttt{aba}$ 的后缀 $\texttt{a}$ 相对而言就多出现 $2$ 次),这里有一种隐含的“父子关系”的感觉。
根据这个直觉,我们定义一个字符串的 right 集合(也叫 $\text{endpos}$ 集合)为它出现的每个区间的右端点。比如 $\texttt{aba}$ 在 $\texttt{abaababa}$ 的 right 集合是 ${3, 6, 8}$。同理,$\texttt{ba}$ 的 right 集合也是 ${3, 6, 8}$。我们把 right 集合相同的子串称为在同一等价类。不妨把 $a$ 与 $b$ 在同一等价类记作 $a \sim b$。
在一个等价类 $u$ 中,令最长串的长度是 $\text{len}(u)$,最短串的长度是 $\min(u)$。
Lemma 1 不妨设 $\lvert a \rvert \le \lvert b \rvert$。要么 $\text{endpos}(b) \subseteq \text{endpos}(a)$(当且仅当 $a$ 是 $b$ 的后缀),要么 $\text{endpos}(a) \cap \text{endpos}(b) = \varnothing$。
Lemma 2 在一个等价类 $u$ 中,所有串长度刚好覆盖 $[\min(u), \text{len}(u)]$ 区间。
接下来我们刻画前面说的父子关系。在前面的例子中 $\texttt{a}$ 所在的等价类 ${1,3,4,6,8}$,就可以看作是 $\texttt{aba}$ 和 $\texttt{ba}$ 所在的等价类 ${3, 6, 8}$ 的父亲。也就是说 $\text{endpos}$ 的 $\subset$ 关系相当于等价类的父子关系。也因此,这种父子关系构成一棵树,称作后缀链接树,也叫 parent 树。对于一个等价类 $u$,我们记它的父亲为 $fa_u$(有的人记作 $link_u$)。特别地,空串对应的等价类的 $fa$ 为 NULL。
可以发现一个至关重要的性质:等价类的总数是 $O(n)$ 的。可以类比虚树的构造,在已有 $n$ 个叶子($n$ 个后缀)的情况下,这样树最多也只能有 $2n-1$ 个节点。
Lemma 3 $\min(u) = \text{len}(fa_u) + 1$。
* 根据 CF 的那篇文章,$S$ 的后缀链接树是 $S$ 反转后的后缀树(Suffix Tree)。所以也有人把后缀链接树叫做前缀树(Prefix Tree)。
SAM 构造
感性理解一下,以后缀链接树的等价类作为节点产生的 DFA,应当也是最小的 DFA。主要是我不会证。OI-Wiki 说 Myhill–Nerode 定理可以证明这一点。这意味着 SAM 是一个极其优雅的结构——它是字符串与生俱来最小的结构。
SAM 的每个节点都是一个等价类,因此 SAM 的节点数量是 $O(n)$ 的。
对于每一个节点,维护 $\delta$、$fa$ 和 $\text{len}$,不维护 $\text{endpos}$。$\delta(u,c)$ 存在的充要条件是:$u$ 中的至少一个字符串,在加上 $c$ 之后仍然是 $S$ 的子串。
我们采取在线的构造,一开始只有一个空串等价类,每次在字符串末尾添加一个字符并修改 SAM。注意时间复杂度是均摊的。
令 $last$ 表示当前时刻整个字符串 $S$ 所在的等价类。接下来要添加一个字符 $c$,把 $S$ 的 SAM 改造为 $S+c$ 的 SAM。
- 首先必然要新建一个 $S+c$ 所在等价类的节点 $cur$。显然 $\text{len}(cur) = \lvert S \rvert + 1 = \text{len}(last) + 1$。而且 $cur$ 必然在原先的自动机内是不存在的。
- 沿着后缀链接树往上爬。
- 令 $p=last$,若 $\delta(p,c)$ 是 NULL,则 $\delta(p,c) \gets cur$,然后 $p \gets fa_p$ 这样往上爬。
- 重复这个过程直到找到一个有效的 $\delta(p,c)$ 或者 $p$ 是 NULL。
- 若 $p$ 是 NULL 即已经爬到根了还没找到,这种情况只可能出现在加入了一个没出现过的字符,令 $fa_{cur}$ 为根节点即可。
- 若找到了一个 $q = \delta(p,c)$,相对复杂一点。在这里细分一下情况:
Case 1: $\text{len}(q) = \text{len}(p) + 1$
$fa_{cur} \gets q$ 即可。
既然 $\delta(p,c)$ 存在,意味着 $S$ 末尾长为 $\text{len}(p)$ 的后缀的一部分出现位置后面一个字符正好是 $c$ 能接上,这些串(加上 $c$ 之后)的 $\text{endpos}$ 即为 $q$ 这个节点。
$\text{endpos}(cur) \subseteq \text{endpos}(q)$,而且 $q$ 作为第一个找到的点满足 $\text{len}(q)$ 最长,因此 $fa_{cur} \gets q$。
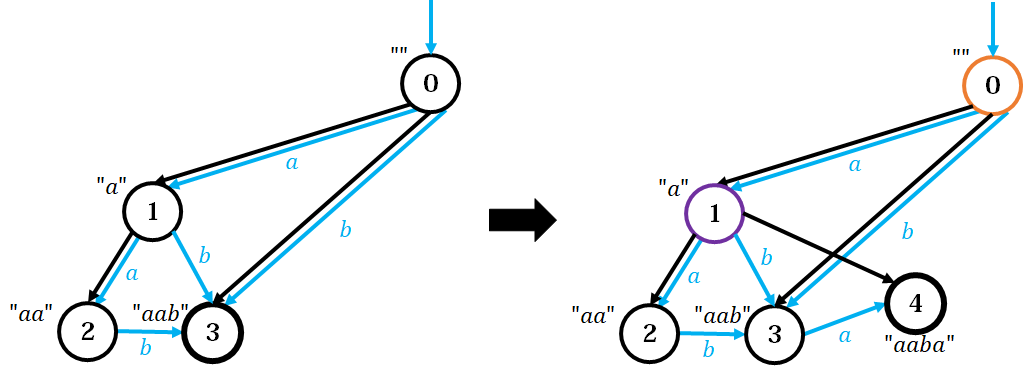
(在 $\texttt{aab}$ 后面插入一个 $\texttt{a}$。黑色是后缀链接树,蓝色是 SAM;橙色是 $p$,紫色是 $q$)
Case 2: $\text{len}(q) > \text{len}(p) + 1$
* 为什么是大于而不是不等于:这个地方不可能出现 $\text{len}(q) < \text{len}(p) + 1$,因为 $\text{len}(p)$ 对应的串 $+c$ 之后一定出现在 $q$ 里。
此时 $q$ 其实混了一堆东西:有从 $\text{len}(p)$ 对应的串 $+c$ 之后得到的 $\text{len}(p) + 1$,也有比 $\text{len}(p)$ 更长的串 $+c$。
必须强行分开这两种。新建一个 $clone$ 节点,继承 $q$ 的 $fa$ 和所有 $\delta$,唯一不同的是 $\text{len}(clone) = \text{len}(p) + 1$。并且将 $fa_q \gets clone$。
与此同时还要通知所有 $p$ 的祖先。从 $p$ 沿着后缀链接树往上爬,令爬到的节点为 $u$,把所有 $\delta(v,c) = q$ 全都改成抵达 $\delta(u,c) = clone$。注意只要有 $\delta(v,c)$ 不存在,$u$ 的所有祖先也不会有 $c$ 的出边,要及时退出。
最后 $fa_{cur} \gets clone$。
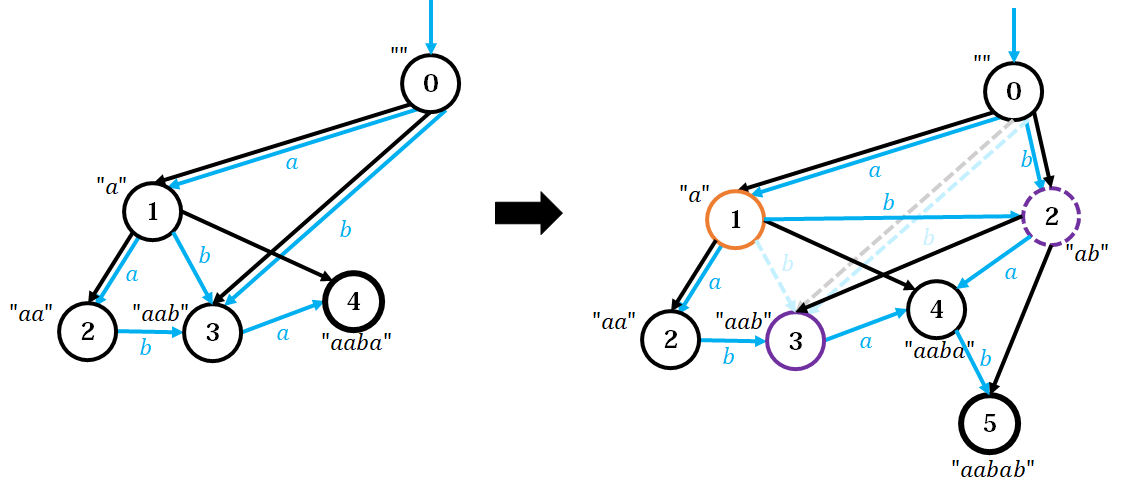
(在 $\texttt{aaba}$ 后面插入一个 $\texttt{b}$。橙色是 $p$,紫色实线是 $q$,紫色虚线是 $clone$)
实现
| 实现 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| 数组 | $O(n)$ | $O(n \lvert \Sigma \rvert)$ |
| 平衡树 | $O(n \log \lvert \Sigma \rvert)$ | $O(n)$ |
| 哈希表 | $O(n)$ | $O(n)$ |
但是 unordered_map 真的常数巨大而且可能被卡,所以这里使用了折中的平衡树 map。后面例题的时间复杂度分析也使用 map 版本。
实践中,小字符集用数组,大字符集用 map,哈希表不用考虑(乐)。
SAM 的节点数量是不超过 $2n-1$ 的,所以要开 $2$ 倍数组。
struct SAM {
int root;
int fa[MAXN * 2], len[MAXN * 2];
map<int, int> nxt[MAXN * 2];
int tot, last;
SAM() {
root = 0;
len[root] = 0, fa[root] = -1;
tot = 0;
last = root;
}
void extend(int c) {
int cur = ++tot;
len[cur] = len[last] + 1;
int p = last;
while (p != -1 and !nxt[p].count(c)) {
nxt[p][c] = cur;
p = fa[p];
}
if (p == -1)
fa[cur] = root;
else {
int q = nxt[p][c];
if (len[q] == len[p] + 1)
fa[cur] = q;
else {
int clone = ++tot;
nxt[clone] = nxt[q];
fa[clone] = fa[q];
len[clone] = len[p] + 1;
fa[q] = fa[cur] = clone;
while (p != -1 and nxt[p][c] == q) {
nxt[p][c] = clone;
p = fa[p];
}
}
}
last = cur;
}
};
时间复杂度证明
结论:$n \ge 2$ 时,SAM 状态数不超过 $2n - 1$;$n \ge 3$ 时,转移数不超过 $3n - 4$。这两个上界都是紧的,构造分别是 $\texttt{abb} \cdots \texttt{bb}$ 和 $\texttt{abb} \cdots \texttt{bbc}$。
TODO:
Ref
名人堂属于是。
- 后缀自动机 (SAM) - OI Wiki
- 后缀自动机 学习笔记 - xht
- 后缀自动机(SAM) - 秋钧
- 算法学习笔记(85): 后缀自动机 - Pecco
- 【补档】后缀自动机学习笔记 - command-block
- 常见字符串算法 II:自动机相关 - qAlex_Weiq
- 后缀自动机(SAM)学习笔记 - ouuan的博客
[后缀自动机学习笔记 Menci’s OI Blog](https://oi.men.ci/suffix-automaton-notes/) [【manim 算法】OI自动机大炒饭(字典树,KMP自动机,AC自动机,后缀自动机,广义后缀自动机)](https://www.bilibili.com/video/BV1uV4y1W7cB/) - A short guide to suffix automata - quasisphere
SAM 维护 endpos
SAM 的节点只维护 $\delta$、$fa$ 和 $\text{len}$,并不直接维护 $\text{endpos}$,但是在一些题目当中我们又确实需要查询 $\text{endpos}$ 相关的信息。
见下面例题中的 P4094 [HEOI2016/TJOI2016] 字符串。
定位子串所在的节点
相当于找 $S_{[1,r]}$ 的祖先中第一个 $\text{len} \ge r-l+1$ 的。倍增即可,时间复杂度 $O(\log n)$。
例题
P3804 【模板】后缀自动机(SAM) (Easy)
求出 $S$ 的所有出现次数不为 $1$ 的子串的出现次数乘上该子串长度的最大值。
$\lvert S \rvert = n \le 10^6$,$\lvert \Sigma \rvert = 26$。
注意到我们要求:
\[\max\limits_{u} \left( [\lvert \text{endpos}(u) \rvert \ne 1] \times \lvert \text{endpos}(u) \rvert \times \text{len}(u) \right)\]问题转化为求 $\lvert \text{endpos}(u) \rvert$。
相当于求 $u$ 在后缀链接树上有几个后代含有 $S_{[1,x]}$,只要每次插入新字符时,创建的新节点 $siz$ 设为 $1$,clone 出来的节点 $siz$ 设为 $0$,DFS 一遍求子树大小即可。
P4070 [SDOI2016] 生成魔咒【强制在线】 (Easy)
有一个空串。$n$ 次操作,每次在串的末尾加一个字符。每次操作结束后求出当前本质不同子串数量。
$n \le 10^5$,$\lvert \Sigma \rvert = 10^9$。
若没有强制在线,这题有 SA 的做法,但是 SAM 的做法是更加自然且显然的。
在 SAM 上,对于一个新的状态 $u$,新加的本质不同子串个数是 $\text{len}(u) - \text{len}(fa_u)$。做完了。
P8368 [LNOI2022] 串
给定一个英文小写字母构成的字符串 $S$,你需要找到一个尽可能长的字符串序列 $(T_0, T_1, \ldots, T_l)$,满足:
- $T_0$ 是 $S$ 的子串;
- $\forall 1 \le i \le l$,$\lvert T_i \rvert - \lvert T_{i - 1} \rvert = 1$;
- $\forall 1 \le i \le l$,存在 $S$ 的一个长度为 $\lvert T_i \rvert + 1$ 的子串 $S’i$,使得 $S’_i$ 的长度为 $\lvert T{i - 1} \rvert$ 的前缀为 $T_{i - 1}$,长度为 $\lvert T_i \rvert$ 的后缀为 $T_i$。
输出这样的字符串序列的长度的最大值(即 $l$ 的最大值)。
多组数据,$1 \le \lvert S \rvert \le 5 \times {10}^5$,$1 \le \sum \lvert S \rvert \le 1.5 \times {10}^6$。
TODO:
P4094 [HEOI2016/TJOI2016] 字符串 (Hard)
超级标准的 SA / SAM 套路题。
给出字符串 $S$,多次询问 $a,b,c,d$ 求 $S_{[a,b]}$ 的所有子串与 $S_{[c,d]}$ 的最长公共前缀的最大值。
$n,m \le 10^5$。$\lvert \Sigma \rvert = 26$。
不管是哪条路,我们都要先发现一个性质,就是答案是有可二分性的。二分一下转成判定性问题。
设 $len$ 为当前二分到的需要判定的长度。
支路 1:SA
LCP 和 SA 是非常搭的。接下来转化问题就要往后缀上靠。
我们现在要找一个 $S$ 的子串 $s$:
- 首先 $s$ 的开头要在 $[a, b - len + 1]$ 内。
- 其次 $\text{lcp}(s, S_{[c,d]}) \ge len$,或者等价说法 $\text{lcp}(s, S_{[c,n]}) \ge len$,转化成后缀问题(顺便清掉了 $d$ 这个变量)。
- 不难发现,在 $sa$ 的顺序上,这是一个包含 $rk_c$ 的连续区间。再二分一次求出这个区间 $[l,r]$,用 height 数组判定。
接下来我们要查询 $sa_{[l,r]}$ 内是否有 $[a, b - len + 1]$ 内的任何一个数。
对于这个问题我们可能会想到离线扫描线,但是二分是不能离线的!所以只能在线可持久化线段树。
二分套可持久化线段树,时间复杂度 $O(M(n) + m \log^2 n)$($M(n)$ 为搭建 SA 的时间复杂度),与 $\lvert \Sigma \rvert$ 无关。
Ref:
- [HEOI2016/TJOI2016]字符串(后缀数组+二分+主席树/后缀自动机+倍增+线段树合并) - Owen_codeisking
- 题解 P4094 【[HEOI2016/TJOI2016]字符串】 - shadowice1984
支路 2:SAM
SAM 这么强大,肯定还是得试试的!
我们要判断 $s_{[c, c + len - 1]}$ 是否在 $s_{[a,b]}$ 出现过。都建出 SAM 了,放到后缀链接树上考虑一下。
首先要找到 $s_{[c, c + len - 1]}$ 所在的状态 $u$,倍增即可。
接下来我们想要知道是否 $\text{endpos}(u) \cap [a + len - 1, b] = \varnothing$。但是上面讲 SAM 的时候我们好像没有维护 $\text{endpos}$ 啊?
SAM 是可以维护 $\text{endpos}$ 的!$\text{endpos}$ 相当于一个值域数组,我们要给树上每个节点都开一个值域数组,这样的需求用线段树合并可以实现。
TODO: 一定写一下!
P4770 [NOI2018] 你的名字 (Lunatic)
牛。
这题的不超纲做法应该是 SA,但是强大的 SAM 依然可以做这题!
给定一个串 $S$。 $q$ 次询问,每次给定一个串 $T$ 和一个区间 $[l,r]$,求 $T$ 有几个本质不同子串没有在 $S_{[l,r]}$ 出现。
$\lvert S \rvert = n \le 5 \times 10^5$,$q \le 10^5$,$\sum \lvert T \rvert \le 10^6$,$\lvert \Sigma \rvert = 26$。
正难则反,我们算 $T$ 有几个本质不同子串在 $S_{[l,r]}$ 出现了。
Subtask: $l=1, r=n$
SAM 是可以维护 $\text{endpos}$ 的!
TODO:
P7361 「JZOI-1」拜神 (Lunatic)
给定一个串 $S$。$q$ 次询问,每次给定一个区间 $[l,r]$,求 $S_{[l,r]}$ 出现至少两次的子串的长度最大值。
$\lvert S \rvert = n \le 5 \times 10^4$,$q \le 10^5$,$\lvert \Sigma \rvert = 26$。
TODO:
广义 SAM
SAM 与广义 SAM 的关系,和 (K)MP 与 ACAM 的关系是一样的。
首先要定义广义后缀:Trie 树上的一个叶子 $y$,与它的一个祖先 $x$ 构成的路径 $x \rightsquigarrow y$ 构成一个广义后缀。广义 SAM 压缩的就是广义后缀。
相对应地,修改 $\text{endpos}(u) = {y \vert \exists x \text{ s.t. } x \rightsquigarrow y \in u }$。
广义 SAM 的构造
离线 BFS
和 AC 自动机一模一样。
记录每一个 Trie 节点 $u$ 在 SAM 上的位置 $pos_u$。对于 Trie 上的一条边 $u \xrightarrow{c} v$,从 $pos_u$ 开始 extend,新节点即为 $pos_v$。
以下代码过不了模板题,会被卡常。写成数组的方式即可通过,但是可读性会减少。
struct SAM {
int root;
int fa[MAXN * 2], len[MAXN * 2];
map<char, int> nxt[MAXN * 2];
int tot;
ll ans; // 本质不同子串数量
SAM() {
root = 0;
len[root] = 0, fa[root] = -1;
tot = 0;
ans = 0;
}
// 注意该函数和 extend 大体相同,但是指定构造的初始位置 last,并且返回新建节点
int extend_from(int last, char c) {
// 省略构造部分!
ans += len[cur] - len[fa[cur]];
return cur;
}
};
struct Trie {
int root = 0;
map<char, int> tr[MAXN];
int fa[MAXN];
int tot;
Trie() {
root = 0;
fa[root] = -1;
tot = 0;
}
void insert(string &s) {
int u = root;
for (char c : s) {
if (!tr[u].count(c))
tr[u][c] = ++tot;
fa[tr[u][c]] = u;
u = tr[u][c];
}
}
};
struct GSAM {
SAM sam;
Trie trie;
int pos[MAXN];
void insert(string &s) {
trie.insert(s);
}
void build() {
queue<int> q;
pos[trie.root] = sam.root;
q.push(trie.root);
while (!q.empty()) {
int u = q.front(); q.pop();
for (auto [c, v] : trie.tr[u]) {
pos[v] = sam.extend_from(pos[u], c);
q.push(v);
}
}
}
};
主函数:
int main() { ios::sync_with_stdio(0); cin.tie(0);
int n; cin >> n;
GSAM gsam;
rep(i, 1, n) {
string s; cin >> s;
gsam.insert(s);
}
gsam.build();
cout << gsam.sam.ans << '\n';
cout << gsam.sam.tot + 1 << '\n';
return 0;
}
因为是先插入所有字符串后再构造,所以说它是离线算法。
在线
TODO:
广义 SAM 例题
P4081 [USACO17DEC] Standing Out from the Herd P (Easy)
TODO: