高开省选 Day 6
Published:
老师:1kri
网络最大流
形式化描述
- 容量限制:$0 \le f(u,v) \le c(u,v)$
- 流量守恒:对不是源汇点的 $u$,有 $\sum\limits_{i} f(i,u) = \sum\limits_{j} f(u,j)$
- 在这两个条件下最大化 $\sum\limits_{i} f(S,i)$,即 $\sum\limits_{j} f(j,T)$。
不难发现一个性质,$f(u,v) = -f(v,u)$。因为两边都正着流显然是不优的,可以抵消。
解法
我们不关心实际的 $c$,我们只关心每条边的剩余容量 $c-f$。
我们每次选一条剩余容量为正的边往下走,看看能不能找到一条 $S \rightsquigarrow T$ 的路径,然后找到路径上剩余容量最小的边流满(这个操作叫做增广)。但是为了防止走错我们要建一条反向边,以后可能需要撤销,可以证明这样的方法是正确的。这个方法叫做 Ford–Fulkerson 增广。
Edmonds–Karp 算法给出了一个 $O(nm^2)$ 的做法。不展开。
Dinic 算法给出了一个 $O(n^2 m)$ 的做法。
比 Dinic 效率更高的做法在 OI 中没有实用价值。
Dinic 算法
TODO: 算法具体过程
单位容量网络上,Dinic 的复杂度是 $O(\min(m \sqrt m, n^{\frac 2 3} m))$。
单位容量网络上,除了源汇点以外每个节点都满足要么入度为 $1$ 要么出度为 $1$,Dinic 的时间复杂度为 $O(\sqrt n m)$。
P.S. OI 的场景中似乎并没有魔改 Dinic 算法这样的题目,所以直接背 Dinic 代码当成黑盒用应该也是个不错的选择。
二分图最大匹配:Hopcroft–Karp 算法
给定一张二分图,求其最大匹配:选择尽量多的不相交的边。
令 $n$ 为点数,$m$ 为边数。$n,m \le 2 \times 10^5$。
首先似乎有 bitset 优化匈牙利算法的解法(一篇教程),但是这题数据范围太大了还是只能网络流。
我们把左图的二分图建成一张右图,每条边的容量为 $1$。通过给左右的边加了 $1$ 的限制,使得每个点都只能存在于一条路径中。
时间复杂度 $O(\sqrt n m)$。
二分图最小点覆盖 / 最大独立集:Kőnig 定理
给定一张二分图,求:
- 最小点覆盖:选择最少的顶点,满足每条边至少有一个端点被选。
- 最大独立集:在一张无向图中选择最多的顶点,满足两两之间互不相邻。
Kőnig 定理:二分图最小点覆盖等于最大匹配。
任意图上,最大独立集等于总点数减掉最小点覆盖。(独立集和点覆盖一一对应)
给定最大匹配,构造最小点覆盖和最大独立集
对于最小点覆盖,我们不难发现匹配中的每条边都要选且仅选一个端点。我们设第 $i$ 条匹配边选左部还是右部为一个 bool 变量 $a_i$,跑 2-SAT。
最小点覆盖的补集是最大独立集。
DAG 最小链覆盖
给定一张 DAG,求它的最小链覆盖:选出一些路径使得每个点都属于一条路径,求出最少的路径数量。
$n \le 150$,$m \le 6000$。
一般图上的最小链覆盖是 NP-Hard 的。但是 DAG 的最小链覆盖可以归约到二分图匹配问题。
网络最大流要求的是最大值,但是这题要求一个最小值。我们考虑用尽量多的边把点连成连通块的思路。
建模:把 $S$ 连到每个点,把每个点连到 $T$;每条边可以选或者不选(选的越多越好)容量为 $1$,每个点的流量最多是 $1$。对点的流量限制可以拆点(见例题 P2766 最长不下降子序列问题)。
P.S. 拆点之后不看源汇点我们就得到了一个二分图,本质是归约到二分图最大匹配。
P.P.S. DAG 可以表示偏序关系,根据 Dilworth 定理,DAG 的最小链覆盖等于它的最长反链,也就是说这个题目其实给出了任意偏序集最长反链(也叫宽度,partial order width)的做法。
最小割
给定一个网络,求它的最小割:删掉一些边,使得不存在 $S \rightsquigarrow T$,并且删去边的边权和最小,求这个最小权值。
最大流最小割定理(Max-flow min-cut theorem):最小割等于最大流。
给定最大流,构造最小割
找到从 $S$ 出发,经过剩余容量大于 $0$ 的边能到达的点集,记为 $A$,$A$ 的补集记为 $B$。$A$ 和 $B$ 之间的边就是最小割,可以证明这些边的权值和等于最大流。TODO:
网络流的建模套路
- 求最小值:用尽量多的边把点连成连通块、最小割
- 点有流量限制:拆点
- 见例题 P2766 最长不下降子序列问题。
- 总流量限制:拆源点
- 对选边有限制:把边看成点
网络最大流 例题
由于许多题目较冗长,对于简单的问题不提供简要题意。
P2763 试题库问题【加强版】(Easy)
有 $n$ 道题目和 $m$ 种类别,每个题目可以属于 $a_i$ 个主类别。现在需要从中抽选出 $m$ 道题目组成一套试卷,满足:存在一种给试卷上的题目分配主类别的方法,使得对于每种类别都有 $b_i$ 道题目的主类别是它。
输出一个方案。
这很二分图,建图时题目那一侧的容量设成 $a_i$,类别这一侧的容量设成 $b_i$。
P5030 长脖子鹿放置 (Easy)
我们要求最大独立集,但是一般图最大独立集是 NPC 做不了。
我们发现这张图是二分图,因为我们可以按照所在行的奇偶性分成左部和右部。
P2765 魔术球问题 (Normal)
假设有 $n$ 根柱子,现要按下述规则在这 $n$ 根柱子中依次放入编号为 $1$,$2$,$3$,…的球。
- 每次只能在某根柱子的最上面放球。
- 同一根柱子中,任何 $2$ 个相邻球的编号之和为完全平方数。
计算在 $n$ 根柱子上最多能放多少个球,输出一种方案。
$1 \leq n \leq 55$。
首先二分答案。
我们把所有 $a+b = k^2$ 的 $(a,b)$(其中 $a<b$)连一条边 $a \to b$,然后在这个 DAG 做最小链覆盖即可。
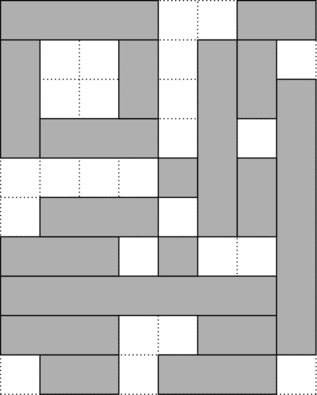
CF1404E Bricks (Normal)
给定一个 $n \times m$ 的网格,网格中有的是黑格有的是白格,要用尽量少的宽度为 $1$ 的砖块盖住黑格,且不能重叠或盖住白格。求砖块数。
$n,m \le 200$。
以下是一个例子:
求最小值,考虑用尽量多的边把点连成连通块的思路。
考虑如果直接建网格图,没有办法刻画“与一个点相连的横边和竖边不能一起选”这样的限制。
我们考虑把边看成点,把横边放在左部,竖边放在右部,跑二分图最大独立集。
CF1592F2 Alice and Recoloring 2 (Hard)
给定一个 $n$ 行 $m$ 列的目标矩阵,矩阵元素只有 $\texttt W$ 或 $\texttt B$,并且你有一个初始矩阵,元素全为 $\texttt W$。现在你可以矩阵实施以下操作:
- 使用 $1$ 块钱,选定一个包含 $(1,1)$ 的子矩阵,把矩阵中的元素全部反转($\texttt W$ 变 $\texttt B$,$\texttt B$ 变 $\texttt W$)。
- 使用 $3$ 块钱,选定一个包含 $(n,1)$ 的子矩阵,把矩阵中的元素全部反转。
- 使用 $4$ 块钱,选定一个包含 $(1,m)$ 的子矩阵,把矩阵中的元素全部反转。
- 使用 $2$ 块钱,选定一个包含 $(n,m)$ 的子矩阵,把矩阵中的元素全部反转。
现在需要你求出把初始矩阵变为目标矩阵最少需要几块钱。 $n, m \le 500$。
发现一个结论:第二和第三个操作没用,因为可以被两次第一个操作直接代替掉。手玩一些样例或许能发现这个结论。
二维差分是显然的。操作 1 是翻转 $4$ 个位置,操作 4 是翻转 $1$ 个位置。
TODO:
P2766 最长不下降子序列问题 (Normal)
给定序列 $a_{[1,n]}$,求能取出几个不重叠的最长不降子序列。
$n \le 500$。
以下为了符合平时做题习惯,用 LIS 代替最长不降子序列,尽管 LIS 原本是最长上升子序列的意思。
我们先求出 LIS 的 DP 数组 $f_i$,表示以 $i$ 结尾的 LIS 长度。
令 $i \prec j$ 表示 $i < j$ 且 $a_i \le a_j$。
令全局 LIS 长度为 $s$。
从 $S$ 向所有 $f_i = 1$ 的 $i$(叫做起点)连边,从 $f_i = s$ 的点(叫做终点)向 $T$ 连边。在所有 $i \prec j$ 且 $f_i + 1 = f_j$ 连边 $i \to j$。这里三处的边的边权都是 $1$。
但是我们还没有保证起点和终点以外的点只能选一次。
我们可以通过拆点的方式限制一个点处的流量。具体来说,我们希望把一个点 $u$ 限流为 $c$,我们把 $u$ 拆成 $in_u$ 和 $out_u$,入边都连到 $in_u$,出边连到 $out_u$,$in_u$ 连一条容量为 $c$ 的边到 $out_u$。
在这题我们就只要 $c=1$ 就行了。
单位网络,$m = O(n^2)$,Dinic 时间复杂度 $O(n^{\frac 8 3})$,可能跑不满,但是不管怎么样 $n \le 500$ 还是能过的。
P2472 [SCOI2007] 蜥蜴 (Easy)
自己做出来了。
超级源点,和上题一样的拆点限制点处的流量,做完了。
P2754 [CTSC1999] 家园 / 星际转移问题 (Normal)
自己做出来了。
二分答案 $T$,我们建一个 $n \times T$ 状态,代表每个点在每个时刻(建边有停留不动和坐太空船两个选项),看看最大流能不能流完 $k$ 个人。
P2057 [SHOI2007] 善意的投票 / [JLOI2010] 冠军调查
TODO:
- 对于第二种冲突,如果投 $1$ 就和 $S$ 连一条容量为 $1$ 的边(代表它在 $),反之亦然。
TODO: 加强?无穷小代价?
P4313 文理分科
TODO:
Hall 定理
令 $G$ 是一个二分图,$X$ 是左部,$Y$ 是右部,且 $\lvert X \rvert \le \lvert Y \rvert$。
对 $W \subseteq X$,记 $N_G(W)$ 为 $Y$ 中所有和 $X$ 中点有边的顶点集合。
Hall 定理:$G$ 的最大匹配等于:
\[\lvert X \rvert - \max\limits_{W \subseteq X} (\lvert W \rvert - \lvert N_G(W) \rvert)\]Hall 定理 例题
CF1373F Network Coverage
TODO:
[ARC076F] Exhausted?
TODO:
最小费用最大流
也称“费用流”。每条边多了一个费用 $w_i$(可正可负),要在达到最大流的前提下使得费用之和 $\sum f_i w_i$ 尽可能小。
TODO:
TODO: 凸性
只要费用最小而不要最大流?
TODO:
要特定总流量?
TODO: