Coriolis Force
Published:
Coriolis 力的推导
对于一个矢量 $\vec{A}$,其在惯性系中对时间的导数和其在旋转系中对时间的导数有以下关系:
\[\left( \frac {d \vec{A}} {dt} \right)_I = \left( \frac {d \vec{A}} {dt} \right)_R + \vec{\omega} \times \vec{A}\]代入 $\vec{A} = \vec{r}$,即质点的位置:
\[\vec{v_I} = \left( \frac {d \vec{r}} {dt} \right)_I = \left( \frac {d \vec{r}} {dt} \right)_R + \vec{\omega} \times \vec{r} = \vec{v}_R + \vec{\omega} \times \vec{r}\]再代入 $\vec{A} = \vec{v}_I$,即质点在惯性系下的速度:
\[\begin{aligned} & \vec{a}_I \\ =& \left( \frac {d \vec{v}_I} {dt} \right)_I \\ =& \left( \frac {d \vec{v}_I} {dt} \right)_R + \vec{\omega} \times \vec{v}_I \\ =& \frac {d} {dt}_R (\vec{v}_R + \vec{\omega} \times \vec{r}) + \vec{\omega} \times (\vec{v}_R + \vec{\omega} \times \vec{r}) \\ =& \vec{a}_R + \left( \frac {d \vec{\omega}} {dt} \right)_R \times \vec{r} + 2 \vec{\omega} \times \vec{v}_R + \vec{\omega} \times (\vec{\omega} \times \vec{r}) \\ \end{aligned}\] \[\boxed{\vec{a}_I = \vec{a}_R + \textcolor{red}{\vec{\omega} \times (\vec{\omega} \times \vec{r})} + \textcolor{limegreen}{2 \vec{\omega} \times \vec{v}_R} + \textcolor{turquoise}{\dot{\vec{\omega}} \times \vec{r}}}\]或者换一个更好看的形式:
\[\boxed{\vec{a}_I = \vec{a}_R - \textcolor{red}{(\vec{\omega} \times \vec{r}) \times \vec{\omega}} - \textcolor{limegreen}{2 \vec{v}_R \times \vec{\omega}} - \textcolor{turquoise}{\vec{r} \times \dot{\vec{\omega}}}}\]红色项被称为离心加速度,绿色项被称为 Coriolis 加速度,蓝色项被称为 Euler 加速度。一般我们考虑的都是参考系匀速转动的情况,所以不会出现 Euler 加速度。
这些加速度分别对应的惯性力为离心力、Coriolis 力和 Euler 力。
例:地转偏向力
地球在匀速自转,在地球的参考系下地球上的运动物体会受到 Coriolis 力。
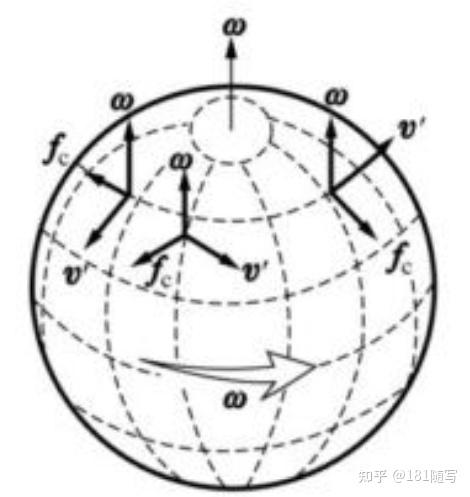
一般来说,$\vec{v}_R$ 与球面相切。从当地上空俯视着看,北半球的 Coriolis 力在 $\vec{v}_R$ 的右偏 $90$ 度方向;南半球的 Coriolis 力在 $\vec{v}_R$ 的左偏 $90$ 度方向;赤道上的 Coriolis 力是竖直的,没有水平的分量。
地球上的足够长的单摆也会受到地球自转的影响。其摆动平面会受地转偏向力影响旋转,在北半球为顺时针,南半球为逆时针,赤道上不会旋转。旋转周期为 $T \approx \frac {2 \pi} {\omega \sin \varphi}$,其中 $\omega$ 为地球自转的角速度,$\varphi$ 为当地纬度。
