动态规划 3
Published:
Slope Trick
TODO:
维护拐点
维护斜率
https://oi-wiki.org/dp/opt/slope-trick/
Minkowski 和
https://oi-wiki.org/geometry/convex-hull/#%E9%97%B5%E5%8F%AF%E5%A4%AB%E6%96%AF%E5%9F%BA%E5%92%8C
$(\min, +)$ 卷积
对凸性封闭,Minkowski 和
TODO:
Slope Trick 例题
P4331 [BalticOI 2004] Sequence (Day1)
TODO:
P11598 [NOISG 2018 Finals] Safety
TODO:
P2748 [USACO16OPEN] Landscaping P (Hard)
TODO:
WQS 二分
全名王钦石二分,最早由王钦石在《浅析一类二分方法》一文中总结。在国外被称为 Aliens Trick。
WQS 二分是一个 2D/1D DP 的优化,用于解决一类问题:有若干个物品,要选取恰好 $m$ 个,在这样的限制条件下最优化一个函数;但是如果没有这样的限制条件则问题很好做。
还需要一个前提条件:令 $f(x)$ 为选择恰好 $x$ 个物品的最优答案,$f$ 具有凸性。
学完做法之后的一个更本质的表述:有一个函数 $f(x)$,给定 $m$,希望求得 $f(m)$,但是 $f$ 的单点值无法快速求。$f$ 有性质:下凸,且对于任意 $\lambda $ 可以快速求 $\min\limits_{x} (f(x) - \lambda x)$。
Method of Lagrange Multipliers
拉格朗日乘数法用于解决“满足 $c(x) = 0$ 时,求 $f(x)$ 的极值”这样的问题。思路是构造拉格朗日函数 $L(x, \lambda) = f(x) - \lambda c(x)$,观察其导数(梯度)的表现,通过这种手段把限制融入目标函数。这样的思想非常有用,我们现在希望找一个离散情况的类比。
在我们这个问题中,我们发现目标的 $f$ 函数很不好求。我们可以将 $f(m)$ 转化为:令 $c(x) = x - m$,限制 $c(x) = 0$ 时 $f(x)$ 的极值(个人感觉这一步转化是最神奇的)。
构造拉格朗日函数 $L(x, \lambda) = f(x) - \lambda c(x) = f(x) - \lambda \cdot (x - m) = (f(x) - \lambda x) + \lambda m$。
$\lambda$ 这一侧平凡,重点关注 $x$ 这一侧。为了求解 $f$ 的极值,我们要求解 $\min\limits_{x} L(x, \lambda)$,这可以转化为 $\min\limits_{x} (f(x) - \lambda x) + \lambda m$。我们记 $b(\lambda) = \min\limits_{x} (f(x) - \lambda x)$ 以及 $p(\lambda) = \arg \min\limits_{x} L(x, \lambda)$。注意直接这样定义的话 $p$ 可能不是单射,所以随便处理一下,比如若合理的 $p$ 有多个则取最大的一个。
为了求解极值,我们关注 $L$ 对 $x$ 的偏差分(前向差分,$\Delta f(x) = f(x+1) - f(x)$):
\[\Delta_x L(x, \lambda) = \Delta f(x) - \lambda\]$L$ 最小,即左边差分小于等于 $0$,右边差分大于等于 $0$:
\[\begin{cases} \Delta_x L(x-1, \lambda) \le 0 \\ \Delta_x L(x, \lambda) \ge 0 \\ \end{cases}\] \[\begin{cases} \Delta f(x-1) - \lambda \le 0 \\ \Delta f(x) - \lambda \ge 0 \\ \end{cases}\] \[\Delta f(x-1) \le \lambda \le \Delta f(x)\]当 $\Delta f$ 具有单调性,即 $f$ 具有凸性的时候,可以保证 $p(\lambda)$ 不会有“跳格”的情况,即对于任意 $x$ 必存在 $\lambda$ 使得刚才的不等式成立,没有无解的情况(但是这不意味着必定存在 $\lambda$ 使得 $p(\lambda) = x$,具体见后文 Corner Case 部分)。
与此同时可以导出 $p(\lambda)$ 单调,可以二分 $\lambda$,找到 $p(\lambda^) = m$,然后直接求解 $f(m) = b(\lambda^) + \lambda m$。
换一个角度来说,$b(\lambda)$ 是原问题在没有个数限制且每选一个物品就有 $-\lambda$ 代价的情况,往往是非常好做的。注意在求解 $b(\lambda)$ 的同时,我们记录 $p(\lambda)$ 用于刚才的二分。令这一步的时间复杂度为 $T(n)$。
二分多 1log,整个问题花费 $O(T(n) \log V_\lambda)$ 的时间可以完成。
几何意义
已知 $f$ 具有凸性,不妨假设 $f$ 的函数图像形成一个下凸包(二阶差分恒非负)。
我们用一个斜率为 $\lambda$ 的直线切凸包,切点为 $(p, f(p))$,可得一个截距 $b(\lambda) = f(p) - \lambda p$,即 $f(p) = b(\lambda) + \lambda p$。而由于前面的推导过程可知 $b$ 和对应的 $p$ 是容易求的。
因此我们希望找到一条切线正好切过 $(m, f(m))$ 这个点,这样可以通过截距反求出函数值。不难发现这个是可二分的。
Corner Case: 三点共线
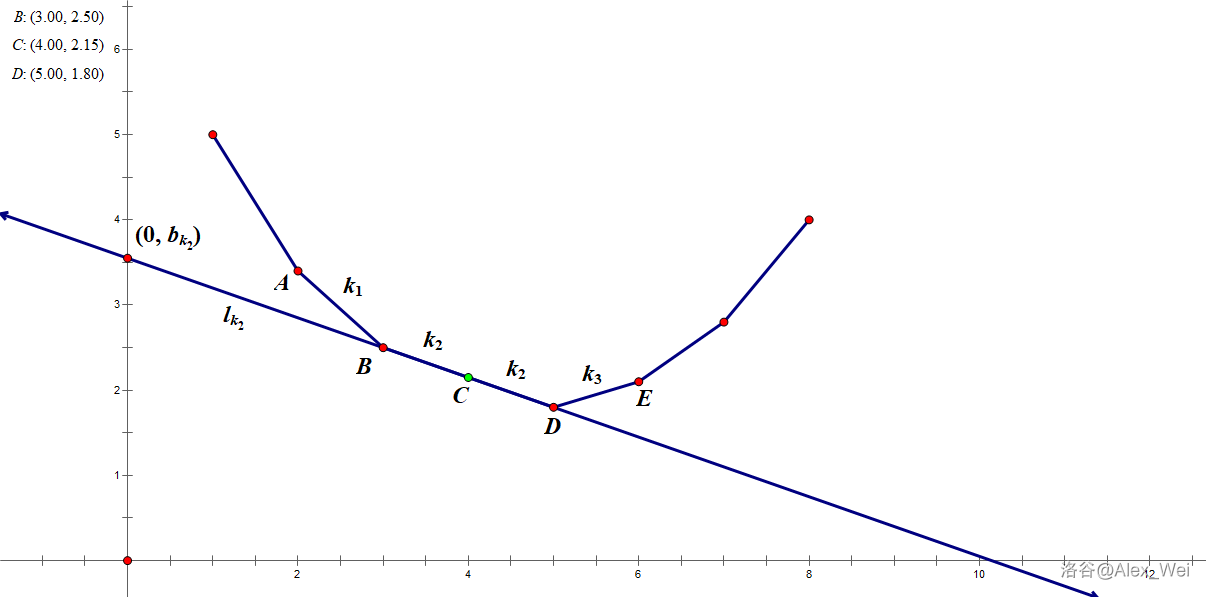
我们想要的 $(m, f(m))$ 在点 C。但是我们用图上这根直线只能切到点 D,但是斜率偏小一点点又只能切到点 B。
在上面的解题过程中,我们对于 $p(\lambda)$ 有多个的情况取了最大的一个。因此我们只要找到使得切点坐标 $\ge m$ 的最小斜率即可,是一个 lower_bound。
注意这里是下凸的情况,上凸时可以类似讨论(TODO: 是 upper_bound 吗)。
Ref
WQS 二分 例题
P1484 种树
给定一条 $n$ 个点的链,每个点有权值 $a_i$(可以为负),求点数最多为 $k$ 的最大权独立集。
$n \le 3 \times 10^5$,$\lvert a_i \rvert \le 10^6$。
环上版本,且限制改为恰好为 $k$:P1792 [国家集训队] 种树。
https://www.luogu.com.cn/discuss/984984
TODO:
P6246 [IOI 2000] 邮局 加强版 加强版 (Lunatic)
https://www.cnblogs.com/Itst/p/12805678.html
TODO:
P5633 最小度限制生成树
TODO:
P2619 [国家集训队] Tree I
TODO:
P5308 [COCI 2018/2019 #4] Akvizna
TODO:
无视 $k$
$f_n$ 是 $n$ 个对手的最多奖金
\[f_i = \max\limits_{0 \le j < i} (f_j + \frac {i-j} i)\] \[f_i = 1 + \max\limits_{0 \le j < i} (f_j - \frac 1 i \times j)\]