动态规划优化 2
Published:
凸函数
下文中“凸函数”默认指“下凸函数”。
凸函数的定义
函数图像上任意两点的连线上的任意一点在函数图像围成的区域内,则这是一个凸函数。
翻译成符号:对于下凸函数,$\forall x, y$ 和 $\forall \alpha \in (0,1)$ 都有
\[f(\alpha x + (1 - \alpha) y) \le \alpha f(x) + (1 - \alpha) f(y)\]
TODO: 斜率单调不减
凸函数的非负线性组合也是凸函数。即:取系数 $\alpha, \beta \ge 0$,凸函数 $f,g$ 的非负线性组合 $\alpha f + \beta g$ 也是凸函数。在离散的情形中,其差分即为 $\Delta(\alpha f + \beta g) = \alpha \Delta f + \beta \Delta g$。
Minkowski 和
https://oi-wiki.org/geometry/convex-hull/#%E9%97%B5%E5%8F%AF%E5%A4%AB%E6%96%AF%E5%9F%BA%E5%92%8C TODO:
点集 $P$ 和点集 $Q$ 的 Minkowski 和记作 $P+Q$,也是一个点集。定义为 $P + Q = {a + b \mid a \in P, b \in Q}$,其中 $a + b$ 就是普通的向量加法。


为什么我们要关注这个运算?不仅因为这个定义很自然,更是因为它和凸包有很好的性质:
- 两个凸集 $P,Q$ 的 Minkowski 和 $P+Q$ 也是凸集。
- $P+Q$ 的边集是 $P$ 的边集和 $Q$ 的边集的按极角排序归并的结果。
证明:
根据凸集的定义,我们只要证明:$\forall r_1, r_2 \in P + Q$,其连线的任意一点也在 $P + Q$ 内。设 $r_1 = p_1 + q_1$,$r_2 = p_2 + q_2$($p_1, p_2 \in P$,$q_1, q_2 \in Q$)。
令 $\alpha \in (0,1)$ 为一个参数,则 $r_1, r_2$ 连线上的任意一点可以表示为 $\alpha r_1 + (1 - \alpha) r_2 = \alpha p_1 + (1 - \alpha) p_2 + \alpha q_1 + (1 - \alpha) q_2$。
因为 $P,Q$ 是凸集,所以 $\alpha p_1 + (1 - \alpha) p_2 \in P$,$\alpha q_1 + (1 - \alpha) q_2 \in Q$。因此它们的和在 $P + Q$ 中,第一条结论证毕。
TODO: 第二条结论
求解两个凸集的 Minkowski 和,只需要分别极角排序然后归并即可。时间复杂度 $O(\lvert P \rvert + \lvert Q \rvert)$,一点损耗都没有。
放一个我一直很想写的例题吧:
给定两个凸包 $P,Q$,$T$ 次询问,每次询问给定一个平移向量 $\vec x$,求 $Q + \vec x$ 和 $P$ 有没有交。
$n = \lvert P \rvert \le 10^5$,$m = \lvert Q \rvert \le 10^5$,$T \le 10^5$。
等价于求 $\vec x$ 是否属于 $P - Q$,其中减号表示 Minkowski “差”。显然两个凸包的 Minkowski “差”还是凸包。
问题转化为给定一个凸包,多次询问判断一个向量是否在给定凸包内。我们可以对凸包极角排序,然后二分极角,单次时间复杂度 $O(\log (n+m))$。
总时间复杂度 $O((n+m) + T \log (n+m))$。
$(\min, +)$ 卷积
两个函数 $f,g$ 的 $(\min, +)$ 卷积 $h$ 定义为:
\[h(x) := \min_y (f(y) + g(x-y))\]凸函数的 $(\min, +)$ 卷积还是凸函数。几何意义上,$h$ 的函数图像是 $f,g$ 函数图像的的 Minkowski 和。
Slope Trick
对于一个分段且每一段都是一次函数的凸函数,我们可以维护拐点或每段斜率来记录这个凸函数。基于这样的想法,我们可以把一个凸函数设成 DP 中的状态。
但是假设有 $n$ 个状态,凸函数需要 $m$ 个数据来记录,则总复杂度 $O(nm)$ 显然不可接受,所以一般来说会用类似滚动数组的方式,即直接从上一个状态转移下来以避免大量的内容复制。
这样的 DP 方式我们称为 Slope Trick。
一般直接想 Slope Trick 是比较困难的。一般的思路是先想二维 DP,然后发现其中一维是凸的,把这一维改成凸函数使用 Slope Trick。
维护斜率跳跃点
若每段斜率离散且值域不大($O(n)$),则我们可以维护导函数的跳跃点。我们规定每一个跳跃点处导函数 $+1$。
注意只有跳跃点的话我们依然无法确定导函数的值,因为可以上下平移。因此一般的做法是记录哪一段是导函数为 $0$ 的区域,即分两个数组,一边记录导函数 $<0$ 部分的跳跃点,一边记录导函数 $>0$ 部分的跳跃点。
举个例子,$\lvert x \rvert + \lvert x-1 \rvert$ 分为三段,$(0,1)$ 这段导函数是 $0$,因此我们记录以下信息:
- 左侧跳跃点:${0}$
- 右侧跳跃点:${1}$
左侧跳跃点最大值和右侧跳跃点最小值之间的部分就是导函数为 $0$ 的部分。
一个小细节:怎么维护 $\lvert x-1 \rvert$ 这样的函数?导函数一下跳了 $2$ 格,记录两次即可。具体来说,记录左侧跳跃点 ${1}$,右侧跳跃点 ${1}$,记录 $2$ 次 $x=1$ 的位置表示 $x=1$ 处导函数 $+2$。
一般来说,右侧跳跃点记作 $\xi_1, \xi_2, \cdots$,左侧跳跃点记作 $\xi_{-1}, \xi_{-2}, \cdots$。导函数为 $0$ 的区间即为 $(\xi_{-1}, \xi_1)$。
维护斜率
https://oi-wiki.org/dp/opt/slope-trick/
TODO:
Slope Trick 例题
P4331 [BalticOI 2004] Sequence (Day1) (Normal)
给定长度为 $n$ 的整数序列 $a$,求一个严格递增整数序列 $b$ 使得 $\sum\limits_{i=1}^n \lvert a_i - b_i \rvert$ 最小。输出最小值和一种方案。
$n \le 10^6, 0 \le a_i \le 2 \times 10^9$。
- 更优雅的版本,且题解更全面:P4597 序列 sequence
- 本题和 CF865D Buy Low Sell High 本质相同,证明见帖子。
首先有一个转化:$b_i$ 严格递增等价于 $b_i - i$ 弱增。这让后面的推导更自然优雅。
以下讨论中,$a_i \gets a_i - i$,$b_i \gets b_i - i$。
考虑 Slope Trick DP。
设状态函数
\[f_i(x) = \min_{b_1 \le \cdots \le b_i \le x} \sum\limits_{j=1}^i \lvert a_j - b_j \rvert\]DP 方程为:
\[f_i(x) = \min_{y \le x} f_{i-1}(y) + \lvert a_i - y \rvert\] \[f_0(x) = 0\]很容易注意到 $\forall i$ 有 $f_i$ 下凸且弱降,答案为 $f_n(\infty) = \min\limits_x f_n(x)$。
实现
首先求 $g(y) := f_{i-1}(y) + \lvert a_i - y \rvert$。相当于在 $f_{i-1}$ 上把 $(-\infty, a_i]$ 段的导数 $-1$,$[a_i, \infty)$ 段的导数 $+1$。
接下来求 $f_i(x) = \min_{y \le x} g(y)$,这等价于 $g$ 和 $0_{[0,\infty)}$ 的 $(\min, +)$ 卷积。从 Minkowski 和的视角来看,这相当于推平 $g$ 的所有导数 $> 0$ 的部分。
此时平衡树已经可以维护维护斜率,但是注意到导数变化很小,维护跳跃点更简单(导数值域 $O(n)$,因此跳跃点个数 $O(n)$):
- 加上 $\lvert a_i - y \rvert$ 相当于在 $a_i$ 处放两个跳跃点。
- 推平导数 $> 0$ 的部分,需要查询最大的跳跃点。这可以用优先队列维护。
输出方案
$\forall i$ 有 $f_i$ 弱降,所以最终的 $\xi_{-1}$ 就是 $b_n$ 的一个最优解。
接下来问题变为求出 $\min_{x \le b_n} f_{i-1}(x)$ 的最优解。这个就 trivial 了。设 $f_{i-1}$ 的最小值在 $p$ 处首次取到:
- $p \le b_n$,则最小值不变。$b_{n-1}$ 最优解为 $p$。
- 否则 $f_{i-1}$ 在 $b_n$ 左侧严格降,在 $x = b_n$ 取到最小值。$b_{n-1}$ 最优解为 $b_n$。
综上所述,$b_{n-1}$ 最优解为 $\min(p, b_n)$。后面归纳下去做就行了。
时间复杂度 $O(n \log n)$。
代码
简单到极致!
// pq 是一个大根堆
rep(i, 1, n)
a[i] -= i;
rep(i, 1, n) {
pq.push(a[i]);
pq.push(a[i]);
pq.pop();
p[i] = pq.top();
}
b[n+1] = INF;
per(i, n, 1)
b[i] = min(p[i], b[i+1]);
rep(i, 1, n)
a[i] += i, b[i] += i;
P11598 [NOISG 2018 Finals] Safety (Normal)
同上题,但是修改限制:去除 $b$ 严格递增的限制,改为 $\forall i, \lvert b_i - b_{i-1} \rvert \le h$。
只需要输出答案,不需要输出方案。
$n \le 2 \times 10^5$,$0 \le a_i \le 10^9$,$0 \le h \le 10^9$。
仿照上题设计状态。但是上题 $b_i \le x$ 这个不适用了,我们现在修改为 $b_i = x$:
\[f_i(x) = \min_{b_1 \le \cdots \le b_i = x} \sum\limits_{j=1}^i \lvert a_j - b_j \rvert\]DP 方程:
\[f_i(x) = \lvert a_i - x \rvert + \min_{\lvert y - x \rvert \le h} f_{i-1}(y)\]边界情况 $f_0(x) = 0$,答案为 $\min_x f_n(x)$。
实现
$\min_{\lvert y - x \rvert \le h} f_{i-1}(y)$ 可以看成 $f_{i-1}$ 与 $0{[-h, h]}$ 的 $(\min, +)$ 卷积。考虑几何意义 Minkowski 和,本质上是把导数为 $0$ 的部分加长 $2h$——把 $f{i-1}$ 导数 $<0$ 的部分向左平移 $h$,导数 $>0$ 的部分向右平移 $h$。
$\lvert a_i - x \rvert$ 依然通过插入两个 $a_i$ 处的跳跃点实现。
两边都用优先队列维护即可,要对于两边分别打全局平移标记。
与此同时要注意我们维护的是导数,要还原原来的函数 $f_i$ 还需要记录一个常数信息,不妨记录最小值。初始时是 $0$,考虑如何更新。
$(\min, +)$ 卷积部分不影响最小值;只有加法部分影响,对 $a_i$ 分类讨论,是否落在常数的 $[\xi_{-1}, \xi_1]$ 范围内:
- 落在常数上:左堆放一个 $a_i$,右堆放一个 $a_i$,不影响最小值。
- 落在 $\xi_{-1}$ 左:左堆放两个 $a_i$,最小值增加 $\xi_{-1} - a_i$。
- 落在 $\xi_1$ 右:右堆放两个 $a_i$,最小值增加 $a_i - \xi_1$。
时间复杂度 $O(n \log n)$。
代码
priority_queue<ll> pq1;
priority_queue<ll, vector<ll>, greater<ll>> pq2;
pq1.push(-INF), pq2.push(INF);
ll tag1 = 0, tag2 = 0; // 向左平移 tag1,向右平移 tag2
ll ans = 0;
rep(i, 1, n) {
tag1 += h, tag2 += h;
ll p = pq1.top() - tag1, q = pq2.top() + tag2;
if (p <= a[i] && a[i] <= q) {
pq1.push(a[i] + tag1);
pq2.push(a[i] - tag2);
} else {
if (a[i] < p) {
pq1.push(a[i] + tag1);
pq1.push(a[i] + tag1);
pq1.pop(), pq2.push(p - tag2);
ans += p - a[i];
} else {
pq2.push(a[i] - tag2);
pq2.push(a[i] - tag2);
pq2.pop(), pq1.push(q + tag1);
ans += a[i] - q;
}
}
}
P2748 [USACO16OPEN] Landscaping P
有 $n$ 个花坛排成一排,第 $i$ 个花坛包含 $a_i$ 泥土,FJ 希望它包含 $b_i$ 泥土。
有 $3$ 种操作:
- 选一个花坛放入 $1$ 泥土,花费 $X$。
- 选一个花坛去掉 $1$ 泥土,花费 $Y$。
- 选花坛 $i,j$,将花坛 $i$ 的 $1$ 泥土运到花坛 $j$,花费 $Z \lvert i - j \rvert$。
求最小总开销。
$n \le 10^5$,$0 \le a_i, b_i \le 10$,$0 \le X,Y \le 10^8$,$0 \le Z \le 1000$。
TODO:
WQS 二分
全名王钦石二分,最早由王钦石在《浅析一类二分方法》一文中总结。在国外被称为 Aliens Trick。
WQS 二分是一个 2D/1D DP 的优化,用于解决一类问题:有若干个物品,要选取恰好 $m$ 个,在这样的限制条件下最优化一个函数;但是如果没有这样的限制条件则问题很好做。
还需要一个前提条件:令 $f(x)$ 为选择恰好 $x$ 个物品的最优答案,$f$ 具有凸性。
学完做法之后的一个更本质的表述:有一个函数 $f(x)$,给定 $m$,希望求得 $f(m)$,但是 $f$ 的单点值无法快速求。$f$ 有性质:下凸,且对于任意 $\lambda $ 可以快速求 $\min\limits_{x} (f(x) - \lambda x)$。
Method of Lagrange Multipliers
拉格朗日乘数法用于解决“满足 $c(x) = 0$ 时,求 $f(x)$ 的极值”这样的问题。思路是构造拉格朗日函数 $L(x, \lambda) = f(x) - \lambda c(x)$,观察其导数(梯度)的表现,通过这种手段把限制融入目标函数。这样的思想非常有用,我们现在希望找一个离散情况的类比。
在我们这个问题中,我们发现目标的 $f$ 函数很不好求。我们可以将 $f(m)$ 转化为:令 $c(x) = x - m$,限制 $c(x) = 0$ 时 $f(x)$ 的极值(个人感觉这一步转化是最神奇的)。
构造拉格朗日函数 $L(x, \lambda) = f(x) - \lambda c(x) = f(x) - \lambda \cdot (x - m) = (f(x) - \lambda x) + \lambda m$。
$\lambda$ 这一侧平凡,重点关注 $x$ 这一侧。为了求解 $f$ 的极值,我们要求解 $\min\limits_{x} L(x, \lambda)$,这可以转化为 $\min\limits_{x} (f(x) - \lambda x) + \lambda m$。我们记 $b(\lambda) = \min\limits_{x} (f(x) - \lambda x)$ 以及 $p(\lambda) = \arg \min\limits_{x} L(x, \lambda)$。注意直接这样定义的话 $p$ 可能不是单射,所以随便处理一下,比如若合理的 $p$ 有多个则取最大的一个。
为了求解极值,我们关注 $L$ 对 $x$ 的偏差分(前向差分,$\Delta f(x) = f(x+1) - f(x)$):
\[\Delta_x L(x, \lambda) = \Delta f(x) - \lambda\]$L$ 最小,即左边差分小于等于 $0$,右边差分大于等于 $0$:
\[\begin{cases} \Delta_x L(x-1, \lambda) \le 0 \\ \Delta_x L(x, \lambda) \ge 0 \\ \end{cases}\] \[\begin{cases} \Delta f(x-1) - \lambda \le 0 \\ \Delta f(x) - \lambda \ge 0 \\ \end{cases}\] \[\Delta f(x-1) \le \lambda \le \Delta f(x)\]当 $\Delta f$ 具有单调性,即 $f$ 具有凸性的时候,可以保证 $p(\lambda)$ 不会有“跳格”的情况,即对于任意 $x$ 必存在 $\lambda$ 使得刚才的不等式成立,没有无解的情况(但是这不意味着必定存在 $\lambda$ 使得 $p(\lambda) = x$,具体见后文 Corner Case 部分)。
与此同时可以导出 $p(\lambda)$ 单调,可以二分 $\lambda$,找到 $p(\lambda^) = m$,然后直接求解 $f(m) = b(\lambda^) + \lambda m$。
换一个角度来说,$b(\lambda)$ 是原问题在没有个数限制且每选一个物品就有 $-\lambda$ 代价的情况,往往是非常好做的。注意在求解 $b(\lambda)$ 的同时,我们记录 $p(\lambda)$ 用于刚才的二分。令这一步的时间复杂度为 $T(n)$。
二分多 1log,整个问题花费 $O(T(n) \log V_\lambda)$ 的时间可以完成。
几何意义
已知 $f$ 具有凸性,不妨假设 $f$ 的函数图像形成一个下凸包(二阶差分恒非负)。
我们用一个斜率为 $\lambda$ 的直线切凸包,切点为 $(p, f(p))$,可得一个截距 $b(\lambda) = f(p) - \lambda p$,即 $f(p) = b(\lambda) + \lambda p$。而由于前面的推导过程可知 $b$ 和对应的 $p$ 是容易求的。
因此我们希望找到一条切线正好切过 $(m, f(m))$ 这个点,这样可以通过截距反求出函数值。不难发现这个是可二分的。
Corner Case: 三点共线
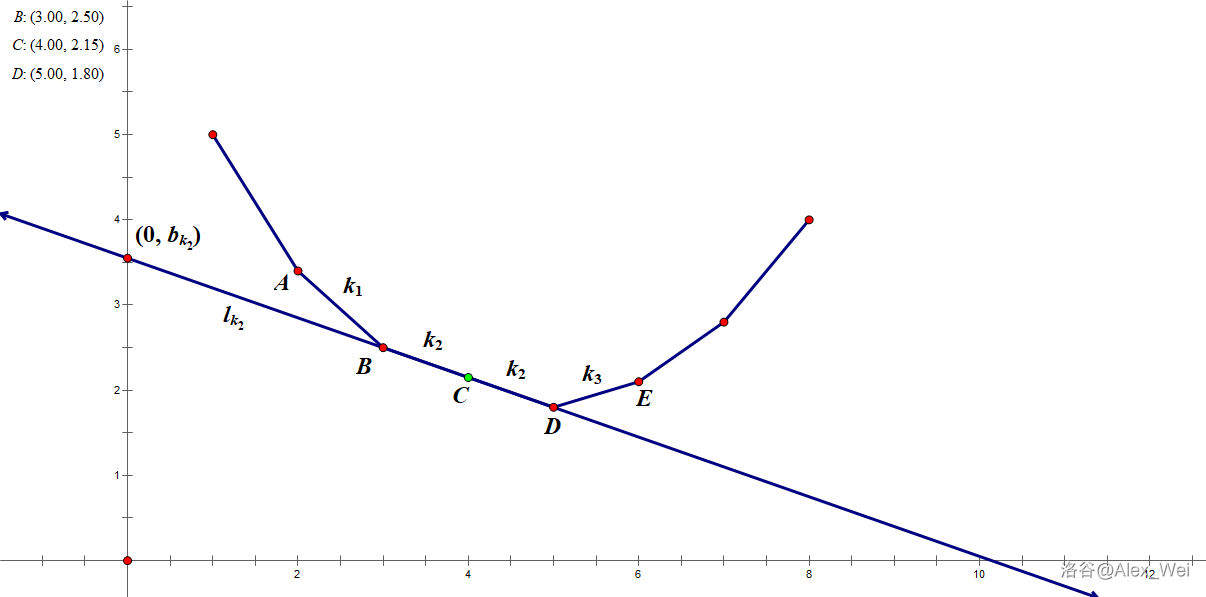
我们想要的 $(m, f(m))$ 在点 C。但是我们用图上这根直线只能切到点 D,但是斜率偏小一点点又只能切到点 B。
在上面的解题过程中,我们对于 $p(\lambda)$ 有多个的情况取了最大的一个。因此我们只要找到使得切点坐标 $\ge m$ 的最小斜率即可,是一个 lower_bound。
注意这里是下凸的情况,上凸时可以类似讨论:找一个使得切点坐标 $\ge m$ 的最大斜率,是一个 upper_bound。
Ref
WQS 二分 例题
例题部分不做凸性证明。
TODO: 重新编排例题顺序。
P1484 种树
给定一条 $n$ 个点的链,每个点有权值 $a_i$(可以为负),求点数最多为 $k$ 的最大权独立集。
$n \le 3 \times 10^5$,$\lvert a_i \rvert \le 10^6$。
环上版本,且限制改为恰好为 $k$:P1792 [国家集训队] 种树。
设 $f(x)$ 为恰好选择 $x$ 个点的答案。最终答案为 $\max_{x \le k} f(x)$。可以证明 $f$ 具有上凸性。
上凸函数取前缀 $\max$ 还是上凸函数。可以看成与 $0_{[0,\infty)}$ 的 $(\max, +)$ 卷积。根据几何意义 Minkowski 和,其实就是推平了右边斜率为负的部分。
直接 WQS 二分即可。为了刚才的推平,一个比较取巧的实现就是二分 $\lambda$ 时直接把二分下界取成 $0$。
二分上界取 $\max \lvert a_i \rvert = 10^6$。TODO:
时间复杂度 $O(n \log V)$。
P6246 [IOI 2000] 邮局 加强版 加强版 (Lunatic)
TODO:
https://www.cnblogs.com/Itst/p/12805678.html
TODO:
P5633 最小度限制生成树
给定一个 $n$ 个点 $m$ 条边的边带权无向图,求一个最小生成树,使得节点 $s$ 连了正好 $k$ 条边。
$n \le 5 \times 10^4$,$m \le 5 \times 10^5$,$k \le 100$。
“恰好 $k$ 条边”很明显是 WQS 二分。根据 WQS 二分的套路,我们可以把与 $s$ 相连的边的边权 TODO: $+ \lambda$ 还是 $- \lambda$,然后跑普通的最小生成树。
这个地方实现得精细一点:注意到我们要多次求最小生成树,我们使用 Kruskal,预先排序,这样每次求解就只有一个 $\alpha$ 的复杂度。具体来说,我们把与 $s$ 相邻的边和与 $s$ 不相邻的边分别排序,对于每次 $\lambda$ 的询问我们归并合成出最后的边的顺序。
时间复杂度 $O(m \log m + m \alpha(m) \log V)$,其中 $V$ TODO:
P2619 [国家集训队] Tree I
TODO:
P5308 [COCI 2018/2019 #4] Akvizna (Easy)
当前局面有 $n$ 个对手。每一轮你可以淘汰一些对手,至少淘汰 $1$ 个。假设当前局面有 $y$ 个对手依然存活,你淘汰 $x$ 个对手,则你获得权值为 $\frac x y$ 的奖励。
你希望在刚好 $k$ 轮之后场上剩 $0$ 个对手。求最大总奖励,保留 $9$ 位小数。
$1 \le k \le n \le 10^5$。
“恰好 $k$ 轮”很明显是 WQS 二分。根据 WQS 二分的套路,我们无视 $k$,设 $f_i$ 为当前局面有 $i$ 个对手,最终的最大总奖励。
\[f_i = \max\limits_{0 \le j < i} (f_j + \frac {i-j} i)\]转化:
\[f_i = 1 + \max\limits_{0 \le j < i} (f_j - \frac 1 i \times j)\]斜率优化即可。斜率 $\frac 1 i$ 单调递减,点的横坐标 $j$ 单调递增,单调队列维护。单次计算时间复杂度 $O(n)$。TODO:
套一层 WQS 二分,总时间复杂度 $O(n \log n)$。TODO: $\lambda$ 值域
https://www.luogu.com.cn/discuss/1087348
