射影几何入门 Day 1
Published:
一篇极度舒适的文章!
射影、无穷远点与无穷远直线
什么是射影?
给定直线 $l$ 和直线 $l’$,可以想象成物体和光屏。以 $P$ 为光源发射光线,则 $l$ 上的每个点 $A$ 都会在 $l’$ 上有一个对应点 $A’$。形式化说,就是直线 $AP$ 与 $l’$ 会产生唯一交点 $A’$。
($P$ 被称为射影中心,$A’$ 被称为 $A$ 的射影)
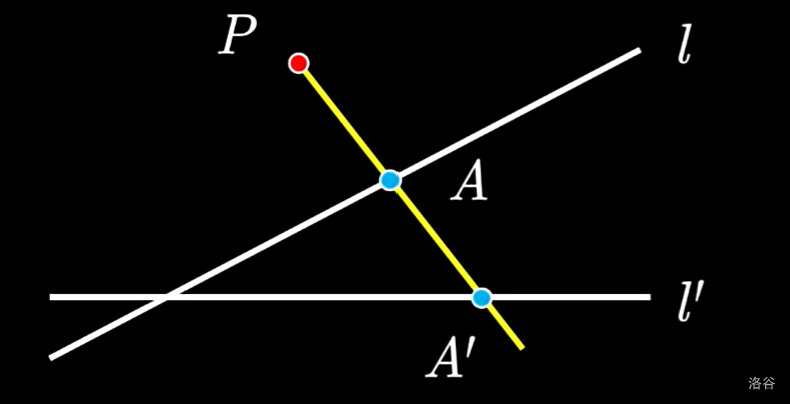
……还是说,并不是?
其实这个图中有两个很不优雅的地方:
- 若光线平行于 $l’$,则此时的 $A$ 根本无法在 $l’$ 上成像;
- 光屏上还存在一个点 $A’$ 满足 $A’P$ 平行于 $l$,$l$ 上的任何一点都无法在光屏的这个位置成像。
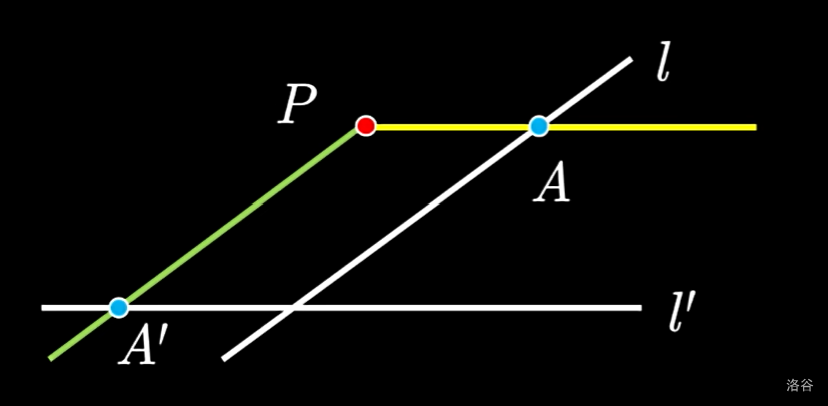
如果我们能把这两个瑕疵补上,这就会让射影成为一个双射。
Desargues 老哥提出了一个天才想法:如果我在每条直线的无穷远处都增加一个无穷远点呢?我们让平行线交于它们的无穷远点,这样就完美地解决了一切问题。
不同方向的平行线拥有不同的无穷远点,这意味着我们要搞一堆无穷远点。这些无穷远点组成了无穷远直线。
“无穷远点构成一条直线”是一个定义。但是很快我们就会看到这个定义的合理性。
总之,加了无穷远元素之后的新世界称为射影平面 $\mathbb P^2$(与 $\mathbb R^2$ 区分),即为原来的欧氏平面加上了无穷远直线。
在射影平面上有很多有趣的性质。比如说,直线变成闭合的了。你可以从一边走到无穷远点,再从另一侧从无穷远点走回来。再比如,原本只有两点确定一直线,现在我们终于有两直线确定一点了。
射影不变性
BV1jc41187Ng【射影几何】“圆锥”曲线为何是双锥?以及初步介绍透视变换(三)
- 结合性
- 共线
- 共点
- 接触性
- 相交
- 相切
- 同素性(一种东西变换完还是这种东西)
- 点
- 直线
- 圆锥曲线(后文会聊)
以下性质无法留存:
- 度量性质
- 角度
- 长度
- 面积
齐次坐标
齐次坐标的构造
射影平面这么优雅的结构,必须想办法用一个代数结构来描述。
原先的欧式坐标显然是不适用的,你不可能给每一个无穷远点都设成类似 $(\infty, \infty)$ 的样子,这没有任何意义。
注意到,无穷远点我们是只在意方向的,也就是说只在意斜率 $\frac y x$……?不,当 $x=0$ 的时候这再次不优雅。但是这启发我们用一种优雅的方式来表示比值。
我们可以不具体计算 $\frac y x$,而是直接用 $x:y$ 这样的比例来表示一个无穷远点。具体来说,$1:2$ 和 $2:4$ 表示同一个无穷远点,而用 $0:1$ 表示直线 $x=0$ 上的无穷远点可以完美解决刚才的问题。
再考虑能不能把有穷的点纳入这套系统。毫无疑问的是我们要再加一维坐标。一个 trivial 的想法是,用 $(x:y, 0)$ 表示无穷远点,用 $(x,y,1)$ 表示有穷的点。但是这显然很诡异。
这时候 Möbius 老哥发力了。他说,既然无穷那里我们只关心比例,那我们能不能也用比例表示有穷点?我可以设一个坐标 $(x:y:z)$ 表示欧式坐标系的 $(\frac x z, \frac y z)$(即我们调整 $x,y,z$ 比例让 $z=1$)。而且这兼容无穷远点,$z=0$ 的时候会 $\div 0$,很像 $\infty$。
齐次坐标就这么诞生啦!$(x:y:z)$ 在 $z=0$ 时表示 $x:y$ 方向上的无穷远点,在 $z \ne 0$ 时表示欧式坐标系的 $(\frac x z, \frac y z)$。特别地,$(0:0:0)$ 没有意义。
普通的欧式坐标其实是齐次坐标的特殊情况,即锁定 $z=1$ 以否认无穷远点的存在。
齐次坐标的真正优势
看起来 $z$ 像是一个莫名其妙加入的指标,但是一旦把它代进一个解析式里,就会有很牛的现象。
比如说,这是一个欧式直线:
\[Ax + By + C = 0\]我们代入齐次坐标:
\[A \frac x z + B \frac y z + C = 0\] \[\boxed{Ax + By + Cz = 0}\]解析式齐次了,$x,y,z$ 竟然是对称的。
对于圆锥曲线也是一样:
\[A x^2 + B xy + C y^2 + D x + E y + F = 0\]会变成
\[\boxed{A x^2 + B xy + C y^2 + D xz + E yz + F z^2 = 0}\]完美的对称性!
事实上,$x,y,z$ 三个坐标本来就是对称的;无穷远并没有任何特殊性。我们非要用欧氏几何的老掉牙思维来套射影平面,才造就了如此不自然的想法。
在圆锥曲线的例子中,我们会对“无穷远没有特殊性”做进一步说明。
另一种严格定义
这个比较简单,而且凸显了对称性。
定义实数三元组的等价关系:
若存在实数 $\lambda$ 使得
\[x_2 = \lambda x_1, y_2 = \lambda y_1, z_2 = \lambda z_1\]则称这两个实数三元组等价
\[(x_1 : y_1 : z_1) \sim (x_2 : y_2 : z_2)\]对于所有实数三元组 $\mathbb R^3$,我们去掉 $(0,0,0)$,并且对于所有的等价类只保留一个元素,我们就得到了射影平面的齐次坐标 $\mathbb P^2$。
这种定义就完全抛弃了落后的欧氏几何,简单地展示了对称性。
一种更好的说法或许是:先有了优雅对称的齐次坐标,而射影平面只是齐次坐标的一种可视化方式。
联立与齐次化
设 $O$ 为坐标原点。有一抛物线 $y^2 = 2px$($p$ 是一个已知常数),有一直线交该抛物线于 $A,B$ 两点,$OA$ 与 $OB$ 斜率乘积 $k_{OA} \times k_{OB} = - \frac 1 2$。
可以证明直线 $AB$ 过一定点,求出这个定点。
* 其实现在我们还不知道什么是抛物线,更不知道 $y^2 = 2px$ 凭什么是抛物线。但是这题并不需要这方面知识。
重写抛物线解析式:
\[y^2 = 2pxz\]设 $AB$ 解析式为 $ax + by = 1$,齐次坐标下为 $ax + by = z$。
由于 $A,B$ 是交点,它们的坐标 $(x:y:z)$ 应满足:
\[\begin{cases} y^2 = 2pxz \\ ax + by = z \\ \end{cases}\] \[\begin{aligned} y^2 = 2px (ax + by) \\ y^2 - 2pbxy - 2pax^2 = 0 \\ \end{aligned}\]注意由于我们使用齐次坐标,得到了一个齐次方程,齐次方程的经典处理手法就是把它变为 $\frac x y$ 或者 $\frac y x$ 的方程,与题目中对斜率的限制不谋而合。
\[(\frac y x)^2 - 2pb \frac y x - 2pa = 0\]这个关于 $\frac y x$ 的二次方程的两根之积是常数 $-\frac 1 2$,显然用 Vieta 定理:
\[\begin{aligned} -2pa = - \frac 1 2 \\ a = \frac 1 {4p} \\ \end{aligned}\]代回解析式 $ax + by = 1$:
\[\frac x {4p} + by = 1\]x-intercept 为 $4p$,即过的定点为 $\boxed{(4p, 0)}$。
如果你是高考玩家,可以写一个“莫名其妙”的构造:
\[\begin{aligned} y^2 = 2px &= 2px \times \textcolor{red}{1} \\ &= 2px \textcolor{red}{(ax + by)} \\ \end{aligned}\]后续做法一致。
我们要对这题进行一些思考。平常圆锥曲线题我们经常会采取联立暴算的方法,一般来说消去的是 $x$ 或 $y$ 指标。
本质上这是在干什么?不妨设我们消 $y$ 指标,我们其实就是不关心竖直方向的信息,以 $y$ 轴无穷远点的视角观察问题。即我们以 $y$ 轴无穷远点为射影中心,把点都投影在 $x$ 轴上。
那么消去 $z$ 是在干嘛?由于 $z$ 是一个比例的信息,我们实际上不关心的是点的具体位置,而只关心方向 $x:y$。即我们以原点 $O$ 为射影中心,把点投影到无穷远直线上。
射影变换
TODO: 重写这段
BV1Wx4y1s7f4 为什么截取圆锥能得到圆锥曲线?- 泰勒猫爱丽丝
对于点 $(x:y:z)$,经过一次射影变换被映射到 $(x’:y’:z’)$。我们要保证相同比例的 $\rho x: \rho y: \rho z$ 会被映射到相同比例的 $\rho x’: \rho y’: \rho z’$。
因此,用矩阵来表示射影变换是合理的:
\[\begin{bmatrix} x' \\ y' \\ z' \end{bmatrix} = \begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix}\]圆锥曲线
我们有一个平面 $\pi$,上面有一个圆 $\Gamma$。我们想研究 $\Gamma$ 射影到另一个平面 $\pi’$ 上能产生的形状。
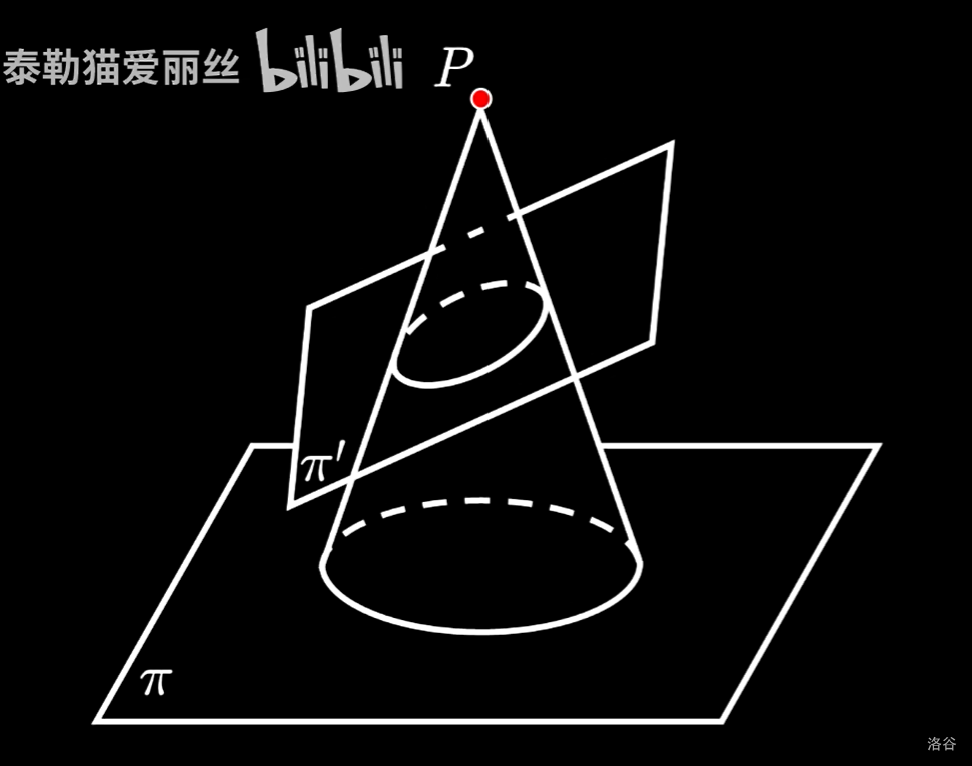
你会发现这个东西也可以被表示为:我有一个双圆锥,我用一个平面去截它,我们要研究截出来线的形状。因此这样产生的形状也被称为圆锥曲线。
注意这个说法是不准确的,因为射影中心还可以是无穷远点,此时会得到一个圆柱而不是圆锥。当然你也可以 argue 一下,说双圆锥和圆柱在射影几何下并没有区别。
直观地看,大部分性质正常的圆锥曲线可以分为三类:椭圆(图 2)、抛物线(图 1)、双曲线(图 3)。

在做解析几何题目的时候,我们会用不同的手法处理这三种曲线。但是这三种曲线真的有什么本质的区别吗?
以双曲线为例,我们可以作出其渐近线 $l_1$ 和 $l_2$,设 $O$ 是它们的交点。
我们可以通过一次射影变换,把 $l_1, l_2$ 变成一对平行线,此时 $O$ 跑到无穷远处,原本的无穷远直线变为了一根正常的直线。并且,双曲线保持与其渐近线的相切关系,变成一个椭圆(关于双曲线为什么和渐近线相切之后会给出严格证明,但是直觉上是显然的)。
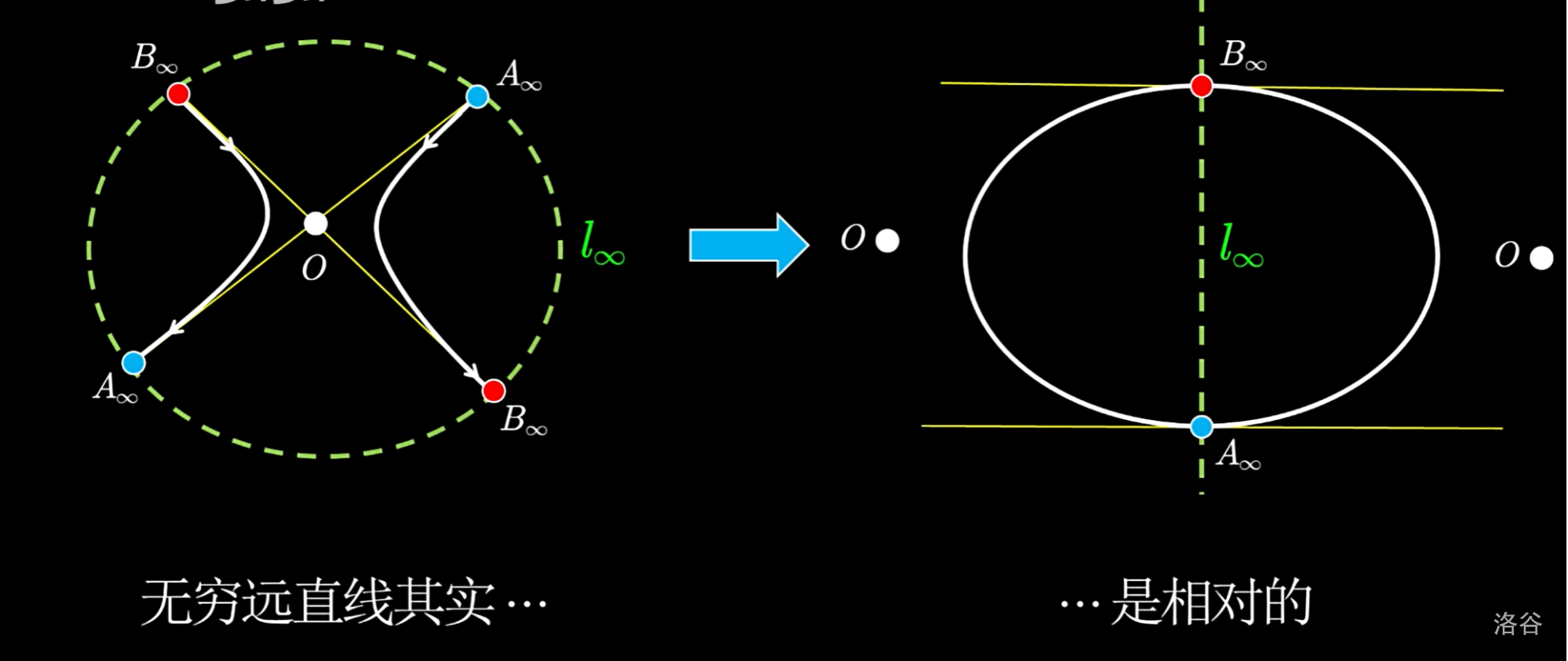
同理,抛物线的两端事实上与无穷远直线相切。我们可以进行一次射影变换把它变成椭圆。
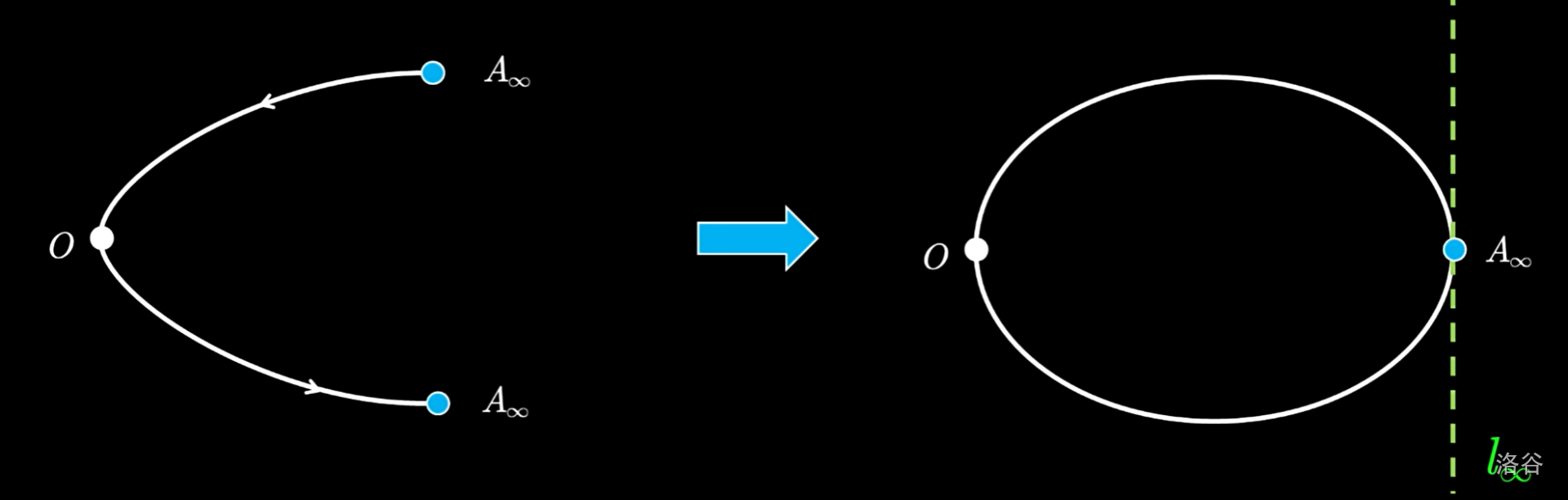
因此,椭圆、抛物线、双曲线的区别实际上就在于它们和无穷远直线的位置关系(相离、相切、相交),三者并没有什么本质区别,都只是属于圆锥曲线而已。做题时,针对不同曲线用截然不同的方法,只是因为我们非要把自己局限于欧氏空间罢了。
圆锥曲线的解析式
我们先写出齐次坐标的单位圆方程:
\[x^2 + y^2 = z^2\]然后我们希望对它进行线性变换。为了方便处理,我们将其写为二次型:
\[\begin{bmatrix} x & y & z \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = 0\]二次型经过一次线性变换之后还是二次型。因此,最后的解析式一定是二次项($x^2, y^2, z^2, xy, xz, yz$)的线性组合:
\[A x^2 + B xy + C y^2 + D xz + E yz + F z^2 = 0\] \[\begin{bmatrix} x & y & z \end{bmatrix} \begin{bmatrix} \textcolor{red}{A} & B/2 & D/2 \\ B/2 & \textcolor{red}{C} & E/2 \\ D/2 & E/2 & \textcolor{red}{F} \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = 0\]根据二次型的理论,我们知道在正交变换下我们可以把 $B$ 的位置变成 $0$。因此,研究很多问题时我们可以直接扔掉 $xy$ 交叉项的系数 $B$,此时便可以轻松使用配方法等技术。
圆锥曲线的类型判别
实在要把自己限制在欧氏空间的话,我们也可以轻易判断欧式圆锥曲线的类型。我们只要求出它和无穷远直线 $z=0$ 的交点个数,也就是直接代入 $z=0$ 求解数。
\[A x^2 + B xy + C y^2 = 0\]解的个数和判别式 $\Delta = B^2 - 4AC$ 有关。
- $\Delta > 0$ 有两个根,与无穷远直线相交两次,即双曲线。
- $\Delta = 0$ 有重根,与无穷远直线相切,即抛物线。
- $\Delta < 0$ 没实根,与无穷远直线相离,即椭圆。
例:一些经典的函数
反比例函数 $y = \frac 1 x$ 的图像是双曲线吗?
解析式
\[xy = z^2\] \[\Delta = 1 > 0\]是双曲线。
对勾函数 $y = x + \frac 1 x$ 的图像是双曲线吗?
解析式
\[xy = x^2 + z^2\] \[x^2 - xy + z^2 = 0\] \[\Delta = 1 > 0\]是双曲线。
圆锥曲线的切线
设圆锥曲线方程为
\[F(x,y,z) = 0\]它是一个等值线,其梯度是它的法向量,而切线与法向量垂直。因此 $(x_0, y_0, z_0)$ 处的切线方程为:
\[\nabla F(x_0, y_0, z_0) \cdot \begin{bmatrix} x - x_0 \\ y - y_0 \\ z - z_0 \end{bmatrix} = 0\]这是一个很暴力的做法。还有一种更加优雅的做法:圆的切线是极其容易计算的,射影变换保持相切不变,因此我可以直接从圆的切线射影到其它圆锥曲线的切线。这种做法可以避免求梯度,方便不会微积分的同学。
不管如何,经过繁琐的计算,我们可以得到:
| 圆锥曲线 | 曲线方程 | 切线方程 | 欧式坐标下 |
|---|---|---|---|
| 椭圆 | $\frac {x^2} {a^2} + \frac {y^2} {b^2} = z^2$ | $\frac {x_0 x} {a^2} + \frac {y_0 y} {b^2} = z_0 z$ | $\frac {x_0 x} {a^2} + \frac {y_0 y} {b^2} = 1$ |
| 双曲线 | $\frac {x^2} {a^2} - \frac {y^2} {b^2} = z^2$ | $\frac {x_0 x} {a^2} - \frac {y_0 y} {b^2} = z_0 z$ | $\frac {x_0 x} {a^2} - \frac {y_0 y} {b^2} = 1$ |
| 抛物线 | $y^2 = 2pxz$ | $y_0 y = p (x_0 z + z_0 x)$ | $y_0 y = p(x_0 + x)$ |
由于双曲线有“渐近线”这种欧氏坐标下比较特别的东西,我们以双曲线为例进行一次计算的示范,并观察其渐近线。
双曲线的切线
\[\frac {x^2} {a^2} - \frac {y^2} {b^2} = z^2\] \[\begin{aligned} F(x, y, z) &= \frac {x^2} {a^2} - \frac {y^2} {b^2} - z^2 \\ \frac {\partial F} {\partial x} (x, y, z) &= \frac {2x} {a^2} \\ \frac {\partial F} {\partial y} (x, y, z) &= - \frac {2y} {b^2} \\ \frac {\partial F} {\partial z} (x, y, z) &= -2z \end{aligned}\]因此在 $(x_0 : y_0 : z_0)$ 处的切线方程为
\[\frac {2x_0} {a^2} (x - x_0) - \frac {2y_0} {b^2} (y - y_0) - 2z_0 (z - z_0) = 0\]化简后即为
\[\boxed{ \frac {x_0 x} {a^2} - \frac {y_0 y} {b^2} = z_0 z }\]双曲线由于延伸到了无穷远,我们好奇它的切线在那里的表现。
我们不难求出双曲线与无穷远直线 $z=0$ 的交点为 $(a![]() 0)$ 和 $(a:-b:0)$。
0)$ 和 $(a:-b:0)$。
直接代入切线方程即可得出
\[\frac x a \pm \frac y b = 0\]即
\[\boxed{ y = \pm \frac b a x }\]其实我们求出的就是双曲线的两条渐近线。