射影几何入门 Day 2
Published:
直线的齐次坐标
这是一条直线的齐次坐标解析式:
\[Ax + By + Cz = 0\]即当我们确定 $A,B,C$ 时,所有满足该式子的 $(x:y:z)$ 就组成了这条直线。
注意 $A,B,C$ 同乘除常数是没有关系的,因此我们依然可以用比例来记。我们就将这条直线标记为比例三元组 $[A:B:C]$(用方括号以和点做区分)。
我们称 $[A:B:C]$ 是这条直线的齐次坐标。
点与直线的对偶 初步
BV1ZH4y1h7vC 定比分点和直线系的关系是什么?- 泰勒猫爱丽丝
点和线其实是一模一样的东西哦。
点列与线束
对于点 $(x_1 : x_2 : x_3)$ 和线 $[A_1 : A_2 : A_3]$,若它们满足
\[A_1 x_1 + A_2 x_2 + A_3 x_3 = \vec A \cdot \vec x = 0\]则说明这个点在这条线上。
我们观察这个式子
\[\vec A \cdot \vec x = 0\]- 固定 $\vec A$ 时,这个方程表示了经过直线 $A$ 的所有点 $x$,称为点列。
- 固定 $\vec x$ 时,这个方程表示了经过点 $x$ 的所有直线 $A$,称为线束。(在其它专题中也称为直线系)
因此这个式子又是点的方程又是线的方程,根据这样的对偶,我们称这个式子体现了点 $x$ 和线 $A$ 的结合关系。
两点求直线 / 两直线求点
\[\begin{cases} A_1 x_1 + A_2 x_2 + A_3 x_3 = 0 \\ A_1 y_1 + A_2 y_2 + A_3 y_3 = 0 \\ \end{cases}\]已知两点 $(x_1 : x_2 : x_3)$ 和 $(y_1 : y_2 : y_3)$。求经过它们的直线的齐次坐标 $[A_1 : A_2 : A_3]$。
用 Cramer 法则可以解出:
\[\frac {A_1} {\begin{vmatrix} x_2 & x_3 \\ y_2 & y_3 \end{vmatrix}} = \frac {A_2} {\begin{vmatrix} x_3 & x_1 \\ y_3 & y_1 \end{vmatrix}} = \frac {A_3} {\begin{vmatrix} x_1 & x_2 \\ y_1 & y_2 \end{vmatrix}}\]选取齐次坐标:
\[[A_1 : A_2 : A_3] = \left[ \begin{vmatrix} x_2 & x_3 \\ y_2 & y_3 \end{vmatrix} : \begin{vmatrix} x_3 & x_1 \\ y_3 & y_1 \end{vmatrix} : \begin{vmatrix} x_1 & x_2 \\ y_1 & y_2 \end{vmatrix} \right]\]这是叉乘运算的定义。因此我们可以记:
\[\vec A = \vec x \times \vec y\]已知两直线 $[A_1 : A_2 : A_3]$ 和 $[B_1 : B_2 : B_3]$,求出其交点 $(x_1 : x_2 : x_3)$。
根据直线和点的对偶关系,你应该已经猜到答案了(证明也是完全一致的):
\[\vec x = \vec A \times \vec B\]虽然这里的解法看起来和叉乘运算有关,可能被限制在 $\mathbb P^2$ 内,但是 Cramer 法则并没有维度的限制,所以其实不必担心。此处只是借用叉乘的记号,为了写得简洁一点而已。
TODO: ChatGPT 说这个东西叫外积。
两点求点列 / 两直线求线束
对于点 $x,y$,有一条直线 $A$ 穿过它们。我希望表示出 $A$ 上的任意一点 $z$,即写出 $A$ 的参数方程。
也相当于求出 $A$ 的点列。
我们把 $x,y$ 看作 $\mathbb P^n$ 中一组方向的基底,则 $z$ 一定是 $x,y$ 张成的子空间中的一个元素,即 $z$ 一定是 $x,y$ 的线性组合:
\[z = \lambda x + \mu y\]对于线 $A,B$,有一个点 $x$ 是它们的公共点。$\lambda A + \mu B$ 有什么意义?
根据对偶,这表示了经过 $x$ 的所有直线 $C = \lambda A + \mu B$。也就是经过点 $x$ 的线束。
自己构造一个射影坐标系
最普通的射影坐标系是如何构造的?
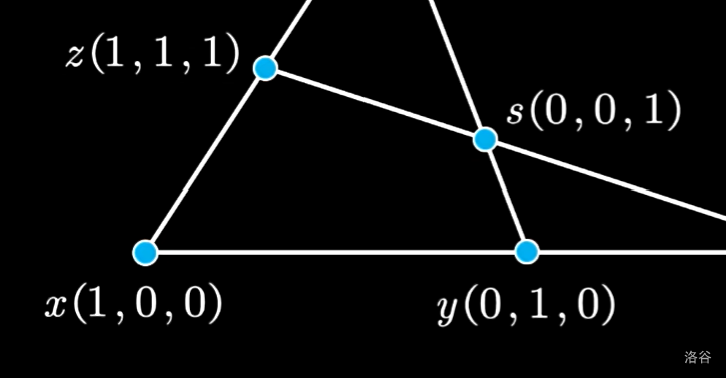
线性代数问题就是搞基找基。考虑 $(1:0:0)$、$(0:1:0)$、$(0:0:1)$ 都有什么意义?
- $(1:0:0)$ 是 $x$ 方向上无穷远点 $x_\infty$。
- $(0:1:0)$ 是 $y$ 方向上无穷远点 $y_\infty$。
- $(0:0:1)$ 是原点。
看起来,只要找到三个点,我就能构造一个射影坐标系?
已知三个点 $x,y,z$ 不共线,是否任何一个点 $w$ 都是 $x,y,z$ 的线性组合?
是。如下构造:
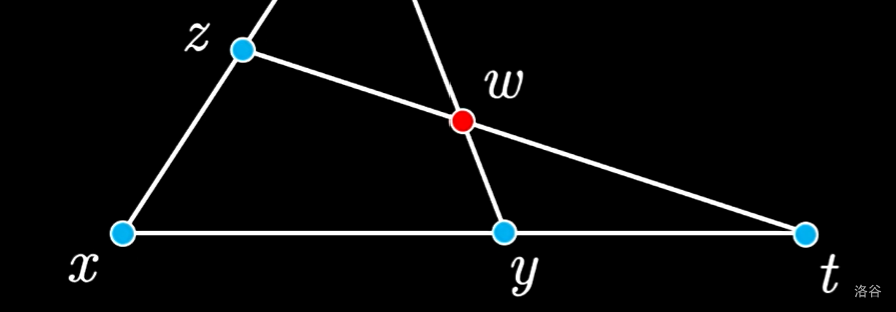
点 $t$ 是 $x,y$ 的线性组合;点 $w$ 是 $z,t$ 的线性组合。显然 $w$ 是 $x,y,z$ 的线性组合。
因此,构造坐标系时,我直接选择三个点分别为我的坐标系下的 $x_\infty, y_\infty, O$ 即可。
线性组合表示的问题
\[x = x_1 (1:0:0) + x_2 (0:1:0) + x_3 (0:0:1)\]这个表示其实有问题,因为三个基向量本身是可以按比例滑动的,这会导致 $x$ 无法确定。
泰勒猫爱丽丝提出了一个办法:在这三点的之外额外设定 $(1:1:1)$ 点即可。此时三个基向量具体取哪组比例会被锁死。
移项法 Trick
对于任何一点 $w$,它可以被表述为三个不共线点 $x,y,z$ 的线性组合。当我们适当调整 $w,x,y,z$ 时,可以满足:
\[w + x + y + z = 0\] \[(x + y) = - (w + z)\]$(x+y)$ 是直线 $xy$ 上的一点,$-(w+z)$ 是 $wz$ 上的一点。因此 $(x+y)$ 就是 $xy$ 与 $wz$ 的交点。
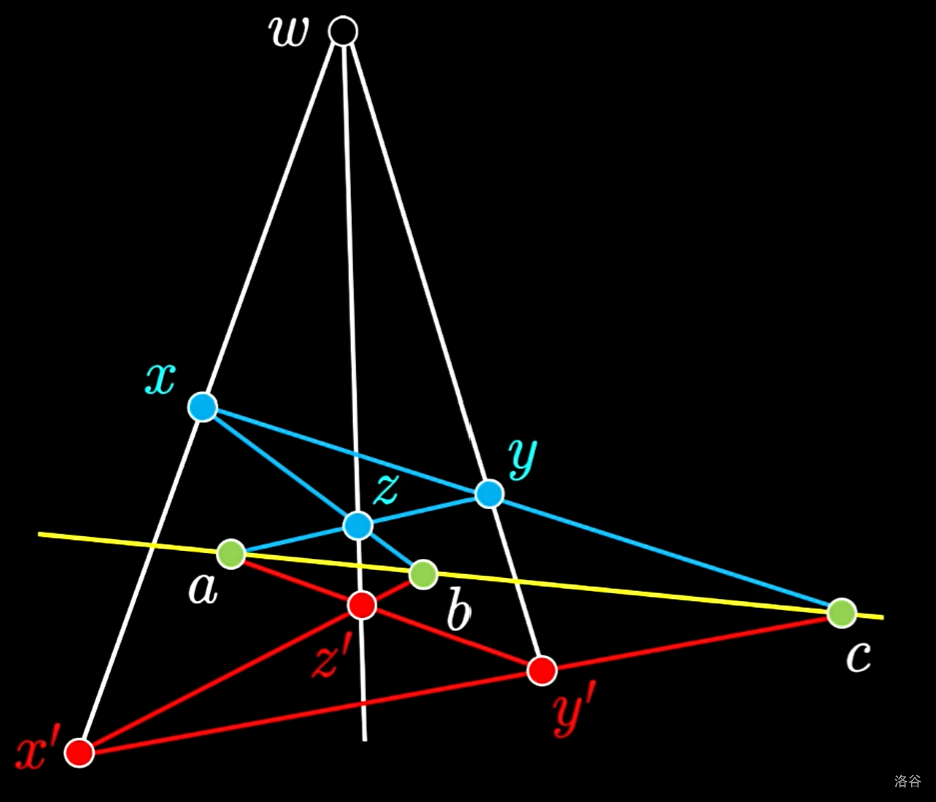
例:Desargues 透视定理与逆定理
有两个三点形 $xyz$ 和 $x’y’z’$。
证明:两个三点形对应点连线共点,当且仅当对应边交点 $a,b,c$ 共线。
我们通过调整 $x’,y’,z’$,可以满足
\[w = x - x' = y - y' = z - z'\]移项法:
\[\begin{cases} y - z = y' - z' = a \\ x - z = x' - z' = b \\ x - y = x' - y' = c \\ \end{cases}\] \[a + b + c = 0\]证完了。由于所有步骤可逆,逆定理也证完了。
如果注意力不好的话,可以以 $x,y,z,w$ 构造射影坐标系,然后叉乘硬算交点。