神秘复变笔记
Published:
Prerequisite Knowledge
几何级数
\[\frac 1 {1 - z} = \sum_{n=0}^\infty z^n\]对复数 $\lvert z \rvert < 1$ 成立。
推论:
\[\frac 1 {a - z} = \sum_{n=0}^\infty \frac {z^n} {a^{n+1}}\]对 $\lvert \frac z a \rvert < 1$ 且 $a \ne 0$ 成立。
Green’s theorem
\[\oint_C P dx + Q dy = \iint_D (\frac {\partial Q} {\partial x} - \frac {\partial P} {\partial y}) dx dy\]人话:矢量场中,边界的曲线积分等于区域内部旋度的积分。
Cauchy-Riemann 条件
设
\[z = x + iy\] \[f(z) = u + iv\]由于复变函数可导需要任意方向导数一致,我们不妨选取 $x$ 和 $iy$ 这两个方向:
\[f'(z) = \frac {\partial u} {\partial x} + i \frac {\partial v} {\partial x}\] \[f'(z) = \frac 1 i (\frac {\partial u} {\partial y} + i \frac {\partial v} {\partial y}) = \frac {\partial v} {\partial y} - i \frac {\partial u} {\partial y}\]对比实部虚部可得 Cauchy-Riemann 条件,这是复变函数可导的必要条件:
\[\boxed{\begin{cases} \dfrac {\partial u} {\partial x} = \dfrac {\partial v} {\partial y} \\ \dfrac {\partial u} {\partial y} = - \dfrac {\partial v} {\partial x} \end{cases}}\]进一步可得 $u,v$ 对 $x,y$ 满足 Laplace 方程:
\[\begin{cases} \nabla^2 u = 0 \\ \nabla^2 v = 0 \\ \end{cases}\]Cauchy 定理
对于区域 $D$ 上的解析函数 $f$,考虑沿着 $C$ 的围道积分:
\[\begin{aligned} & \oint_C f(z) dz \\ =& \oint_C (u + iv) (dx + i dy) \\ =& \oint_C (u dx - v dy) + i (v dx + u dy) \\ =& \oint_C (u dx - v dy) + i \oint_C (v dx + u dy) \\ =& - \iint_D (\frac {\partial v} {\partial x} + \frac {\partial u} {\partial y}) dx dy + i \iint_D (\frac {\partial u} {\partial x} - \frac {\partial v} {\partial y}) dx dy \\ =& 0 \end{aligned}\]根据 Cauchy-Riemann 条件,两个 $\iint$ 都是 $0$。
即任意围道积分为 $0$。
这等价于积分值与路径无关,可以构造 $F(z) = \int_{z_0}^z f(\xi) d\xi$,这就是 $f$ 的原函数。
曲线族 Cauchy 定理
我现在的积分区域又有外边界又有内边界怎么办?
很简单,连一条通道沟通它们,使用 Cauchy 定理,然后让通道宽度 $\to 0$ 即可。
e.g. 这个图有一个小圆是内边界。
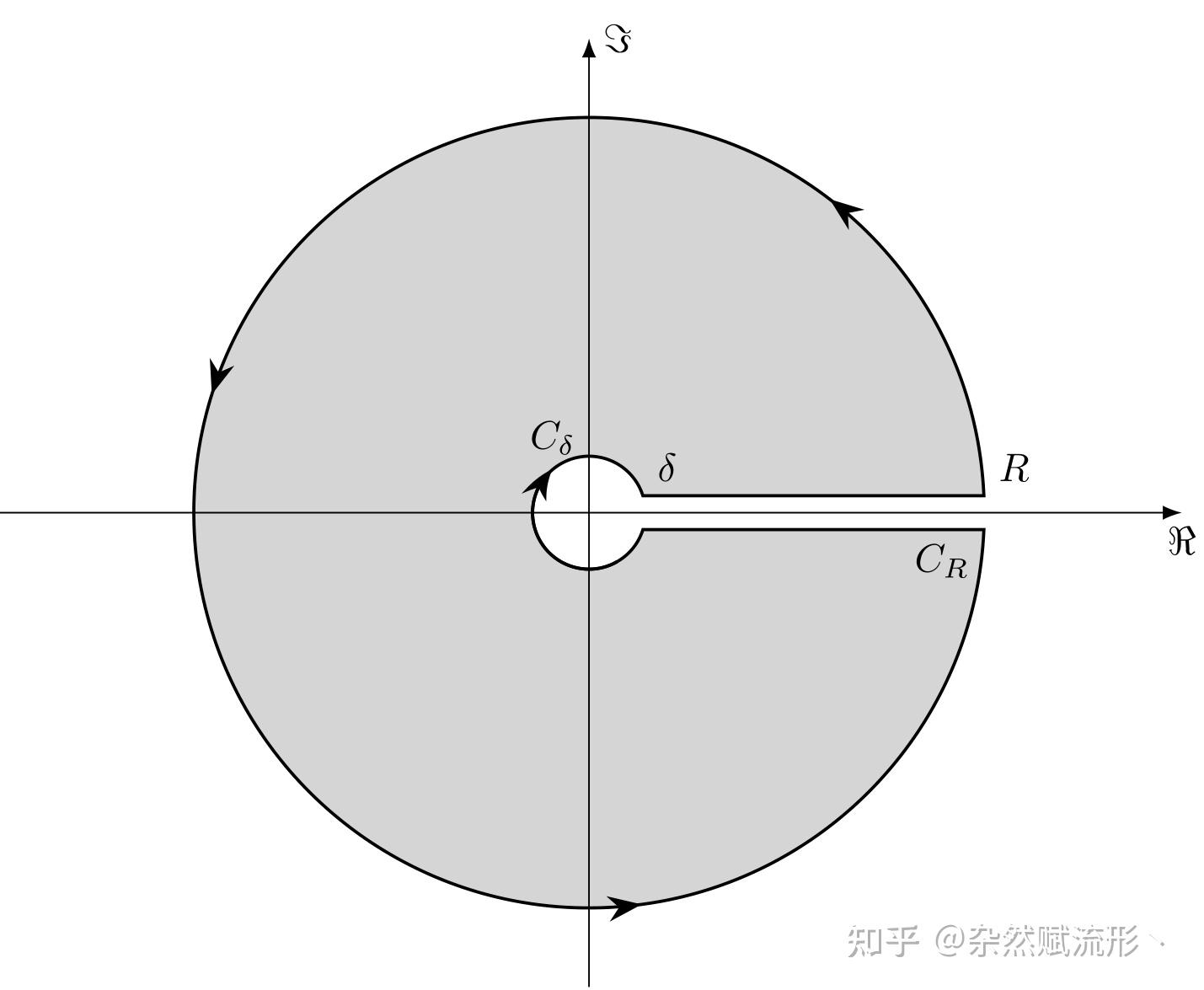
注意内边界的围道是顺时针,积出来是反的。一个小推论:外边界积分等于内边界积分之和。
简单的奇点
哪哪都解析未免性质有点太好了。我们来研究有一个奇点的情况。考察积分
\[\oint_C (z - a)^n dz\]显然它唯一可能的奇点就是 $a$。若围道不包含 $a$ 则啥事没有,直接 $0$。
若包含了 $a$,则我们在里面挖掉一个小圆:
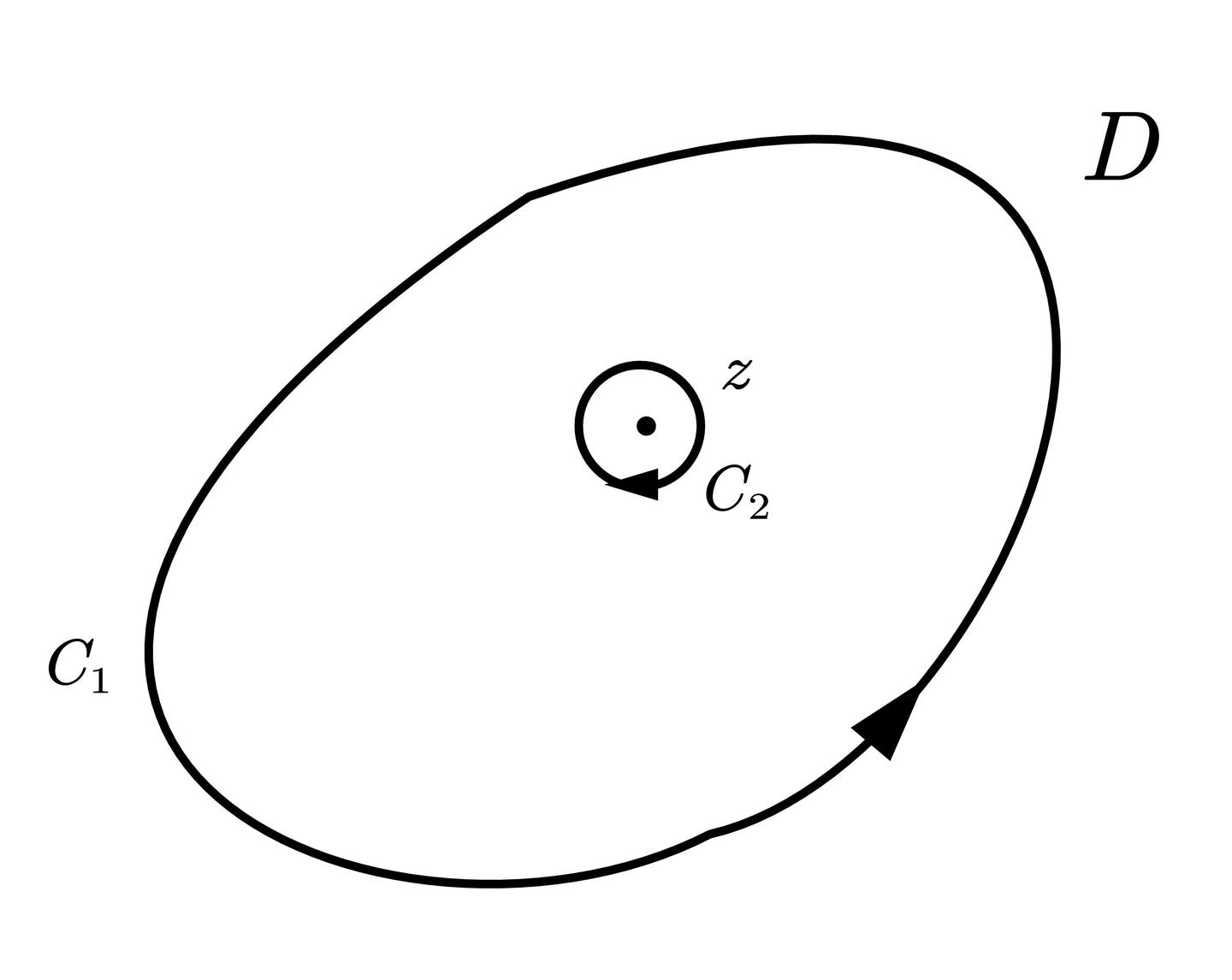
我们对挖完的区域使用 Cauchy 定理,注意内部边界是顺时针:
\[\begin{aligned} \oint_{C_1} (z-a)^n dz &= \oint_{C_2} (z-a)^n dz \\ &= \int_0^{2\pi} r^n e^{i n \theta} d(r e^{i n \theta}) \\ &= i r^{n+1} \int_0^{2\pi} e^{i (n+1) \theta} d\theta \\ &= 2 \pi i [n = -1] \\ \end{aligned}\] \[\boxed{ \oint_C (z - a)^n dz = \begin{cases} 2 \pi i & n = -1 \text{ and } C \text{ encloses } a \\ 0 & \text{otherwise} \\ \end{cases}}\]这可以起到一个类似过滤器的效果。
Residue Theorem 留数定理
根据 Cauchy 定理的推论,外边界围道积分等于内边界围道积分之和:
\[\oint_C f(z) dz = \sum_k \oint_{C_k} f(z) dz\]其中 $C_k$ 是包住了第 $k$ 个奇点 $z_k$ 的围道。
我们定义留数:
\[\text{Res}(f, z_k) := \frac 1 {2 \pi i} \oint_{C_k} f(z) dz\]则这可以被重新表述为:
\[\boxed{ \oint_C f(z) dz = 2 \pi i \sum_k \text{Res}(f, z_k) }\]这就是留数定理。这么个定义看起来很没道理,其实是为了凑下面的东西:
若函数 $f(z)$ 可以被展开为
\[f(z) = \sum_{n = -\infty}^\infty c_n (z - a)^n\]这个级数称为 Laurent 级数,会在后面分析(留数的具体求法也要等到那个时候)。则
\[\begin{aligned} \text{Res}(f, z_k) =& \frac 1 {2 \pi i} \oint_C f(z) dz \\ =& \frac 1 {2 \pi i} \oint_C \left( \sum_{n = -\infty}^\infty c_n (z - a)^n \right) dz \\ =& \frac 1 {2 \pi i} \sum_{n = -\infty}^\infty c_n \oint_C (z - a)^n dz \\ =& c_{-1} & \text{when } C \text{ encloses } a \\ \end{aligned}\]即留数等于 Laurent 级数的 $-1$ 次项系数。
Cauchy 积分公式
我们构造函数
\[g(z) = \frac {f(z)} {z - z_0}\]用一样的思路:

当 $r \to 0$ 时,$f(z_0 + r e^{i \theta}) \to f(z_0)$。因此这个积分趋于 $2\pi i f(z_0)$。
整理得:
\[\boxed{ f(z_0) = \frac 1 {2\pi i} \oint_C \frac {f(z)} {z - z_0} dz }\]称为 Cauchy 积分公式。
为了方便后续讨论,我们更换一下记号:
\[f(z) = \frac 1 {2\pi i} \oint_C \frac {f(\xi)} {\xi - z} d\xi\]高阶导数
我们把两边同时对 $z$ 求导:
\[\frac {df} {dz} = \frac 1 {2\pi i} \oint_C \frac {f(\xi)} {(\xi - z)^2} d\xi\]数学归纳法一下可得:
\[\frac {d^n f} {dz^n} = \frac {n!} {2\pi i} \oint_C \frac {f(\xi)} {(\xi - z)^{n+1}} d\xi\]Liouville 定理
对于一个整个复平面上都解析且有界的函数 $f$,$f$ 是常数函数。
我们让围道是一个半径为 $r$ 的圆,$M(r)$ 为圆上的函数值模长最大值(上确界)。
\[\begin{aligned} & \lvert f^{(n)}(z) \rvert \\ =& \lvert \frac {n!} {2\pi i} \oint_C \frac {f(\xi)} {(\xi - z)^{n+1}} d\xi \rvert \\ \le & \frac {n!} {2 \pi} \frac {M(r)} {r^{n+1}} 2 \pi r \\ =& \frac {n! M(r)} {r^n} \\ \end{aligned}\]在 $r \to \infty$ 时,由于 $M(r)$ 不许 $\to \infty$,因此结果为 $0$。
$f$ 的任意阶导数均为 $0$,因此 $f$ 是常数函数。
代数基本定理
这个小学生都会的定理,终于在大学得到了证明。
(大于等于 $1$ 次的)多项式必有根。
反证法,设 $p(z)$ 是一个没根的多项式。则
\[\frac 1 {p(z)}\]是一个没有奇点,全平面解析的函数。
在 $\lvert z \rvert \to \infty$ 时,$\lvert \frac 1 {p(z)} \rvert \to 0$,因此它也有界。
根据 Liouville 定理,$\frac 1 {p(z)}$ 解析且有界只能是常数函数。因此 $p$ 是常数函数,但是多项式不可能是常数函数,证毕。
Taylor 级数
\[f(z) = \frac 1 {2\pi i} \oint_C \frac {f(\xi)} {\xi - z} d\xi\]我们把这个公式在 $z_0$ 处展开。我们先看
\[\begin{aligned} \frac 1 {\xi - z} &= \frac 1 {(\xi - z_0) - (z - z_0)} \\ &= \sum_{n=0}^\infty \frac {(z - z_0)^n} {(\xi - z_0)^{n+1}} \\ \end{aligned}\](在 $\lvert z - z_0 \rvert < \lvert \xi - z_0 \rvert$ 成立)
\[\begin{aligned} f(z) =& \frac 1 {2\pi i} \oint_C \frac {f(\xi)} {\xi - z} d\xi \\ =& \frac 1 {2\pi i} \oint_C f(\xi) \sum_{n=0}^\infty \frac {(z - z_0)^n} {(\xi - z_0)^{n+1}} d\xi \\ =& \sum_{n=0}^\infty \left( \frac 1 {2\pi i} \oint_C \frac {f(\xi)} {(\xi - z_0)^{n+1}} d\xi \right) (z - z_0)^n \end{aligned}\] \[\boxed{ f(z) = \sum_{n=0}^\infty \frac {f^n(z_0)} {n!} (z - z_0)^n \\ }\]这就是 Taylor 展开式。使用条件为,我们能构造出以下围道:
- $f$ 在围道内解析
- 包含以 $z_0$ 为圆心 $\lvert z - z_0 \rvert$ 为半径的圆(要保证 $\lvert \xi - z_0 \rvert$ 总是大于 $\lvert z - z_0 \rvert$)
因此 Taylor 展开的收敛域是一个大小为 $\lvert z^* - z_0 \rvert$ 的圆,其中 $z^*$ 是离 $z_0$ 最近的奇点。
推论:奇点处无法 Taylor 展开。
Laurent 级数
我们以展开点 $z_0$ 为圆心,用奇点把平面分割为若干环形区域。
对于一个 $z$,设它落在 $r < \lvert z - z_0 \rvert < R$ 的环形区域中。
则可以构造两条围道($C_1$ 在外逆时针 $\lvert \xi - z_0 \rvert > \lvert z - z_0 \rvert$,$C_2$ 在内顺时针 $\lvert \xi - z_0 \rvert < \lvert z - z_0 \rvert$)夹住 $z$:
\[f(z) = \frac 1 {2\pi i} \oint_{C_1} \frac {f(\xi)} {\xi - z} d\xi - \frac 1 {2\pi i} \oint_{C_2} \frac {f(\xi)} {\xi - z} d\xi\]前一个积分直接 Taylor,后一个积分由于不满足 Taylor 的使用条件所以要换个想法。
我们考虑反着展开。思想是把 $z \mapsto \frac 1 z$ 后还是用几何级数:
\[\frac 1 {1 - z} = - \frac 1 z \frac 1 {1 - \frac 1 z} = - \sum_{n=1}^\infty z^{-n}\]具体操作是:
\[\begin{aligned} \frac 1 {\xi - z} &= - \frac 1 {(z - z_0) - (\xi - z_0)} \\ &= - \sum_{n=0}^\infty \frac {(\xi - z_0)^n} {(z - z_0)^{n+1}} \\ \end{aligned}\](在 $\lvert \xi - z_0 \rvert < \lvert z - z_0 \rvert$ 成立)
\[\begin{aligned} & \frac 1 {2\pi i} \oint_{C_2} \frac {f(\xi)} {\xi - z} d\xi \\ =& \frac 1 {2\pi i} \oint_{C_2} f(\xi) \left( - \sum_{n=0}^\infty \frac {(\xi - z_0)^n} {(z - z_0)^{n+1}} \right) d\xi \\ =& \sum_{n=0}^\infty \left(- \frac 1 {2\pi i} \oint_{C_2} f(\xi) (\xi - z_0)^n d\xi \right) (z - z_0)^{-1-n} \\ =& - \sum_{n=-\infty}^{-1} \left( \frac 1 {2\pi i} \oint_{C_2} \frac {f(\xi)} {(\xi - z_0)^{n+1}} d\xi \right) (z - z_0)^n \\ \end{aligned}\]与此同时,我们注意到这些系数与围道无关。因此仅仅对于系数来说,我们可以把 $C_1$ 和 $C_2$ 选择成随意的围道(不需要满足刚才的距离条件,任意一条在环域内包含了 $z_0$ 的围道都可以),干脆选同一条围道 $C$。把公式缝合起来:
\[\boxed{ f(z) = \sum_{n=-\infty}^\infty \left( \frac 1 {2\pi i} \oint_C \frac {f(\xi)} {(\xi - z_0)^{n+1}} d\xi \right) (z - z_0)^n }\]这就是 Laurent 级数。

留数的计算
根据前面的结论,留数就是在奇点 $a$ 处 Laurent 级数的 $-1$ 次项系数(用 $[x^n]f(x)$ 代表 $f$ 的 $n$ 次项系数):
\[\text{Res}(f, a) = [(z-a)^{-1}] f(z)\]首先,若 Laurent 级数不含负幂,则此时称 $a$ 是 $f$ 的一个可去奇点,此时留数是 $0$。如 $0$ 是 $\frac {\sin z} z$ 的可去奇点。
对于一个负幂有限的 Laurent 级数(此时称 $a$ 是 $f$ 的 $m$ 阶极点),设它最小的负幂是 $-m$ 次,则它的 $-1$ 次项系数可以这么表述:
\[\boxed{ \text{Res}(f, a) = \frac 1 {(m-1)!} \lim_{z \to a} \frac {d^{m-1}} {dz^{m-1}} ((z-a)^m f(z)) }\]特别地,$m=1$ 时可以化简为
\[\boxed{ \text{Res}(f, a) = \lim_{z \to a} (z-a) f(z) }\]常用结论:若 $f(z) = \frac {P(z)} {Q(z)}$,$P,Q$ 在 $a$ 的某邻域内解析,$Q(a) = 0$ 且 $Q’(a) \ne 0$(意味着 $m=1$),则
\[\text{Res}(f, a) = \frac {P(a)} {Q'(a)}\]只要注意到 $\lim_{z \to a} \frac {z-a} {Q(z)} = \lim_{z \to a} \frac {z-a} {Q(z) - Q(a)}$ 是导数定义即可。
但是,如果 $m = \infty$(此时称 $a$ 是 $f$ 的本性奇点),这就很坏了。具体问题具体分析。
留数定理计算实积分
复变反杀实变!
Example 1. 计算
\[\int_{-\infty}^\infty \frac 1 {x^6 + 1} dx\]
设 $f(x) = \frac 1 {x^6 + 1}$。
你要是老老实实做原函数那你有的好做了。
我们构造一个半径为 $r$ 的半圆形围道,一会儿我们要让 $r \to \infty$:
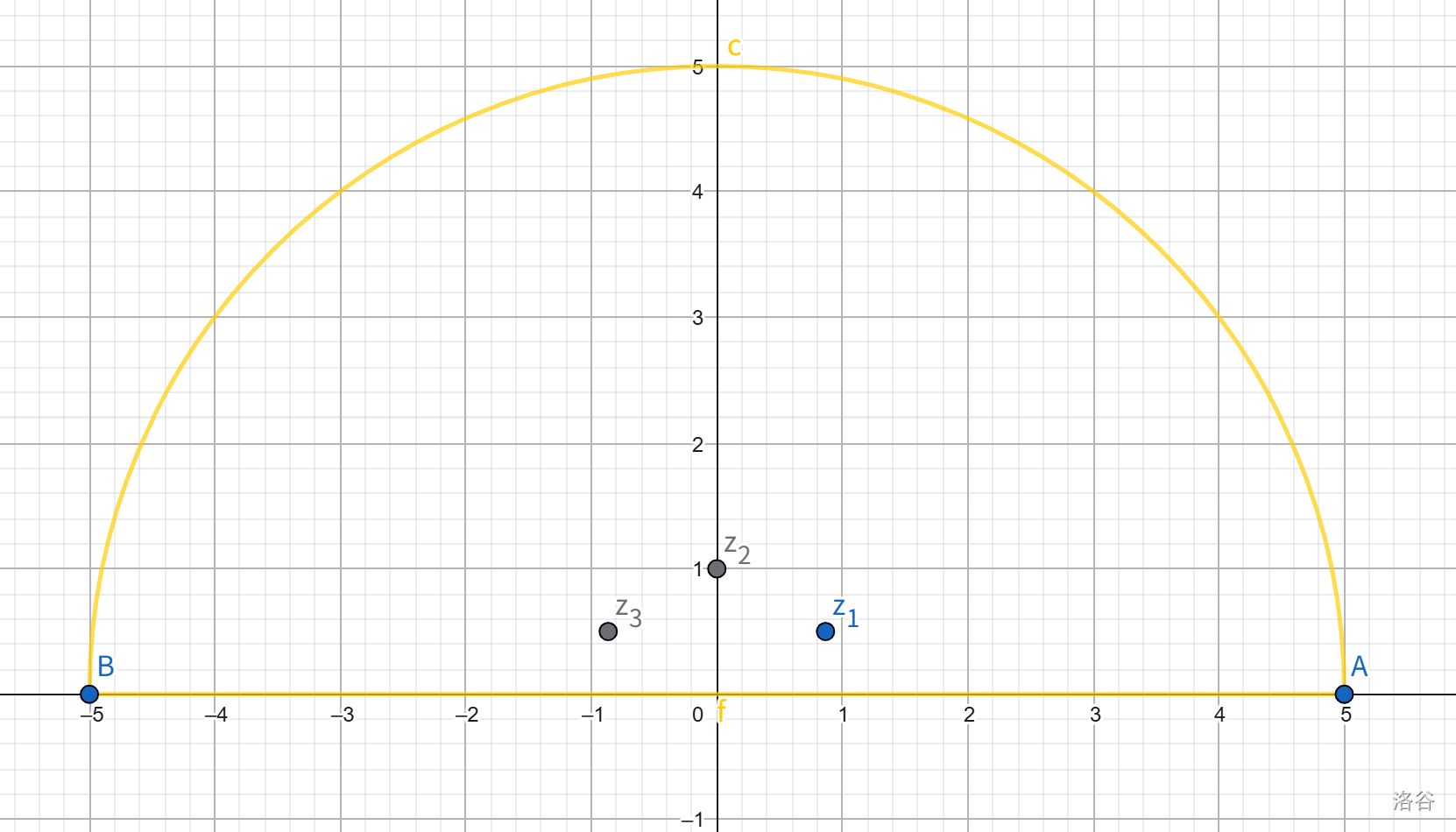
我们令 $c$ 是半圆,$s$ 是底下的线段(忽略图上的标记):
\[\int_c f(z) dz + \int_s f(z) dz = 2 \pi i \sum \text{Res}(f, z_k)\]所求积分
\[\begin{aligned} & \int_{-\infty}^\infty f(x) dx \\ =& \lim_{r \to \infty} \int_s f(z) dz \\ =& 2 \pi i \sum \text{Res}(f, z_k) - \lim_{r \to \infty} \int_c f(z) dz \\ \end{aligned}\]对于半圆弧上的积分,弧长是 $\Theta(r)$ 的,但是分母是 $\Theta(r^6)$ 的,整体 $\Theta(r^{-5})$ 在 $r \to \infty$ 时趋于 $0$。
$f$ 有 $6$ 个奇点,在半圆形内有 $3$ 个一阶极点 $e^{\frac {i \pi} 6}, e^{\frac {3 i \pi} 6}, e^{\frac {5 i \pi} 6}$。
\[\begin{aligned} & \text{Res}(f, z_k) \\ =& \frac 1 {\frac d {dz} (1 + z^6)} \vert_{z=z_k} \\ =& \frac 1 {6 z_k^5} \\ \end{aligned}\]三处留数之和为 $- \frac i 3$。乘上 $2 \pi i$ 得到最终结果:
\[\boxed{\int_{-\infty}^\infty \frac 1 {x^6 + 1} dx = \frac 2 3 \pi}\]对于形如 $\int_{-\infty}^\infty f(x) dx$ 的积分,构造半圆形围道经常是一个好的做法。
Example 2. 计算
\[\int_0^{2\pi} \frac 1 {5 + 4 \cos \theta} d\theta\]
正常做法是万能公式 $\tan \frac \theta 2$,可以算出原函数 $\frac 2 3 \arctan (\frac 1 3 \tan \frac \theta 2) + C$,但是比较麻烦。
令 $z = e^{i\theta}$,我们考虑
\[\cos \theta = \frac {z + z^{-1}} 2\]那我们可以换元,$d \theta = \frac 1 {iz} dz$,构造圆形围道 $\lvert z \rvert = 1$。
\[\begin{aligned} & \int_0^{2\pi} \frac 1 {5 + 4 \cos \theta} d\theta \\ =& \oint_{\lvert z \rvert = 1} \frac 1 {5 + 2 (z + z^{-1})} \frac 1 {iz} dz \\ =& \oint_{\lvert z \rvert = 1} \frac 1 {i (2z^2 + 5z + 2)} dz \end{aligned}\]一阶极点 $z = - \frac 1 2$,留数为 $\frac 1 {i (4z + 5)} \vert_{z=-\frac 1 2} = \frac 1 {3i}$。
最终答案为 $\frac 1 {3i} \times 2 \pi i$,即
\[\boxed{ \int_0^{2\pi} \frac 1 {5 + 4 \cos \theta} d\theta = \frac 2 3 \pi }\]对于三角函数的整周期积分,构造圆形围道经常是一个好的选择。
更多例子:【TikZ实例】留数定理:你想要的积分围道都在这儿 - 杂然赋流形丶
反函数的 Taylor 展开——Lagrange 反演
给定存在反函数的解析函数 $f$ 在 $0$ 处的 Taylor 展开系数,保证 $[x^0]f(x) = 0$ 且 $[x^1]f(x) \ne 0$。
求其反函数 $g$ 在 $0$ 处的 Taylor 展开的各项系数。
首先我们显式写出系数:
\[[y^n] g(y) = \frac 1 {2 \pi i} \oint_C \frac {g(\xi)} {\xi^{n+1}} d\xi\]换元 $\xi = f(x)$(即 $g(\xi) = x$),$d\xi = f’(x) dx$:
\[\begin{aligned} [y^n] g(y) &= \frac 1 {2 \pi i} \oint_C \frac {x f'(x)} {f(x)^{n+1}} dx \\ &= \text{Res}\left( \frac {x f'(x)} {f(x)^{n+1}}, 0 \right) \\ \end{aligned}\]我们希望化简这个留数。有一个观察:任意 Laurent 级数在求导后一定不含 $-1$ 次项($0$ 次项求导会变没而不会变出 $-1$ 次项),因此任意导数形式的东西留数都是 $0$。
我们构造
\[\frac {x f'(x)} {f(x)^{n+1}} = \frac 1 n \frac 1 {f(x)^n} \textcolor{red}{- \frac 1 n \frac d {dx} \left( \frac x {f(x)^n} \right)}\]红色项是一个导数,因此可以直接从留数中去掉:
\[\begin{aligned} [y^n] g(y) &= \text{Res}(\frac 1 n \frac 1 {f(x)^n}, 0) \\ &= \frac 1 n \text{Res}(\frac 1 {f(x)^n}, 0) \end{aligned}\] \[\boxed{ f^{-1}(y) = \sum_{n=1}^\infty \left( \frac 1 n \text{Res}(\frac 1 {f(x)^n}, 0) \right) y^n }\]这个定理称为 Lagrange 反演。等价写法:
\[\boxed{ f^{-1}(y) = \sum_{n=1}^\infty \left( \frac 1 n [x^{-1}]\frac 1 {f(x)^n} \right) y^n }\] \[\boxed{ f^{-1}(y) = \sum_{n=1}^\infty \left( \frac 1 n [x^{n-1}] \left( \frac x {f(x)} \right)^n \right) y^n }\]例:LambertW
\[\begin{aligned} & [y^n] W(y) \\ =& \frac 1 n [x^{n-1}] (\frac x {x e^x})^n \\ =& \frac 1 n [x^{n-1}] e^{-nx} \\ =& \frac 1 n \frac {(-n)^{n-1}} {(n-1)!} \\ =& \frac {(-n)^{n-1}} {n!} \\ \end{aligned}\] \[\boxed{ W(y) = \sum_{n=1}^\infty \frac {(-n)^{n-1}} {n!} y^n }\]实数上的方程
\[y = x e^x\]对于 $y \in [- \frac 1 e, \infty)$ 必定只存在一个 $\ge -1$ 的解,这个解被定义为函数 $W(y)$ 的值。
求出 $W$ 在 $y=0$ 处的 Taylor 展开式。
- 注:显然 $W(0) = 0$。
- 注:$W$ 函数在 Mathematica 中为
ProductLog。
总结
- 这篇文章从复变函数导数出发,导出了 Cauchy-Riemann 条件,这是复变函数导数独有的极好性质;
- 进一步利用 Green 公式导出了复变函数围道积分的 Cauchy 积分公式,并定义了留数;
- 根据 Cauchy 积分公式,得到了 Taylor 展开以及进一步的 Laurent 展开;
- 根据留数是 Laurent 展开 $-1$ 次项系数的性质,找到了留数的计算方法;
- 初步尝试了构造围道后通过留数定理计算实积分的方法;
- 研究了反函数的 Taylor 展开问题,将其与留数挂钩,得到了 Lagrange 反演公式。