圆幂、根轴与根心
Published:
圆幂
有一个圆心为 $O$ 半径为 $r$ 的圆 $\Omega$。有一个点 $P$。
过 $P$ 作一直线 $l$ 与 $\Omega$ 交于 $A,B$。
寻找一个这幅图中的不变量（与 $l$ 无关）。
对于圆中弦的问题，我们作垂径显然是一条不错的辅助线：
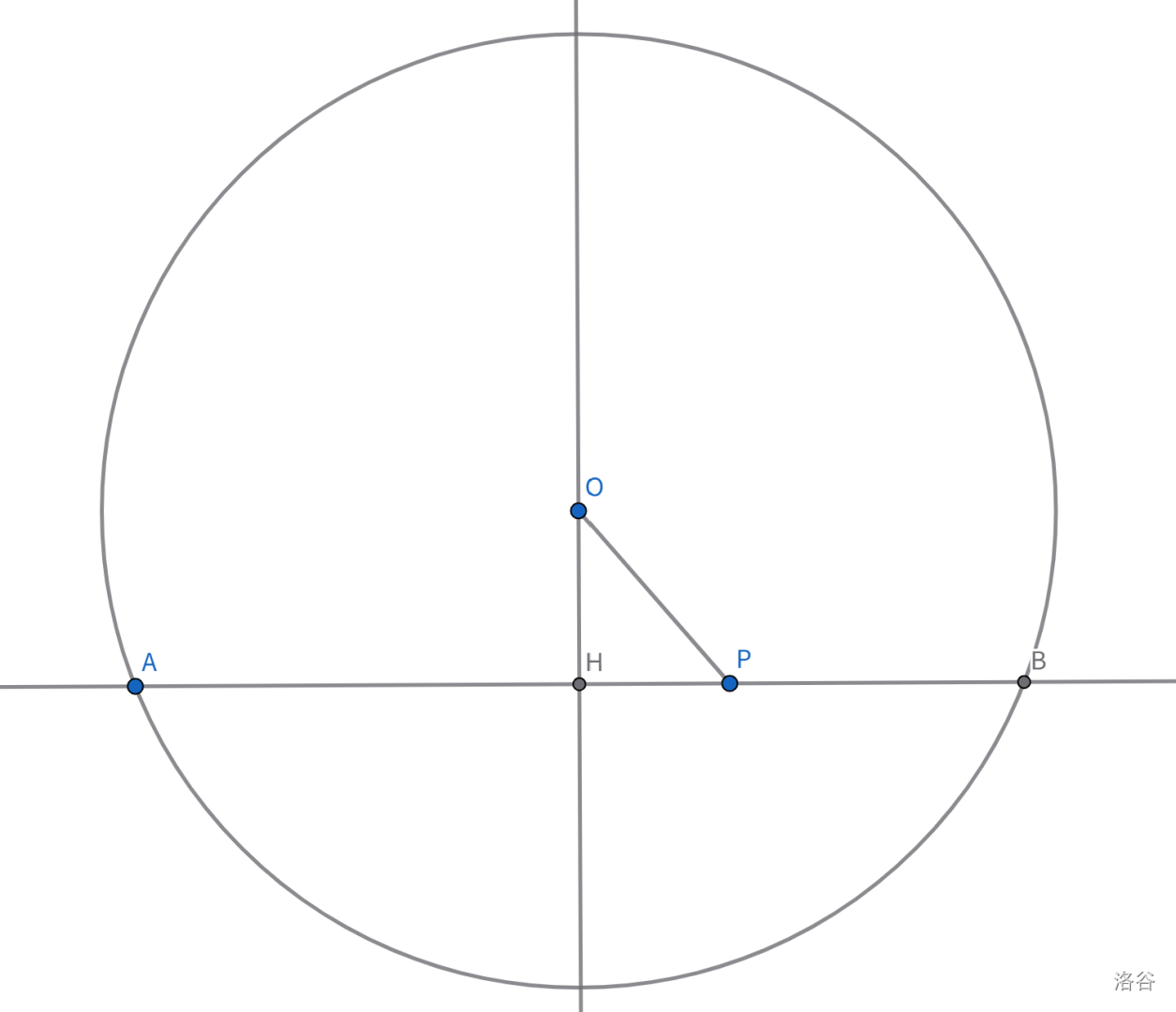
勾股定理可以算出：
- $AH^2 = r^2 - OH^2$
- $PH^2 = OP^2 - OH^2$
很容易想到以下不变量：
\[PH^2 - AH^2 = OP^2 - r^2\]我们尝试把 $PH^2 - AH^2$ 用原图的点表示。以下计算中都是有向线段，以 $A \to B$ 为正方向。（e.g. 在图上的这个例子中 $PA$ 是一条负的线段）
\[\begin{aligned} & PH^2 - AH^2 \\ =& (PH - AH) (PH + AH) \\ =& (PH + HA) (PH + HB) \\ =& PA \times PB \\ \end{aligned}\]我们成功找到了不变量：
\[\boxed{ PA \times PB \equiv OP^2 - r^2 }\]这个公式叫圆幂定理。同时，我们把这个量称为 $P$ 关于圆 $\Omega$ 的圆幂 (power of a point)。记作
\[\boxed{ \Pi(P) = OP^2 - r^2 }\]圆幂的性质
- 若 $\Pi(P) < 0$，说明 $P$ 在圆内。
- 若 $\Pi(P) = 0$，说明 $P$ 在圆上。
- 若 $\Pi(P) > 0$，说明 $P$ 在圆外。
对于圆外的 $P$，$\Pi(P)$ 的几何意义为：
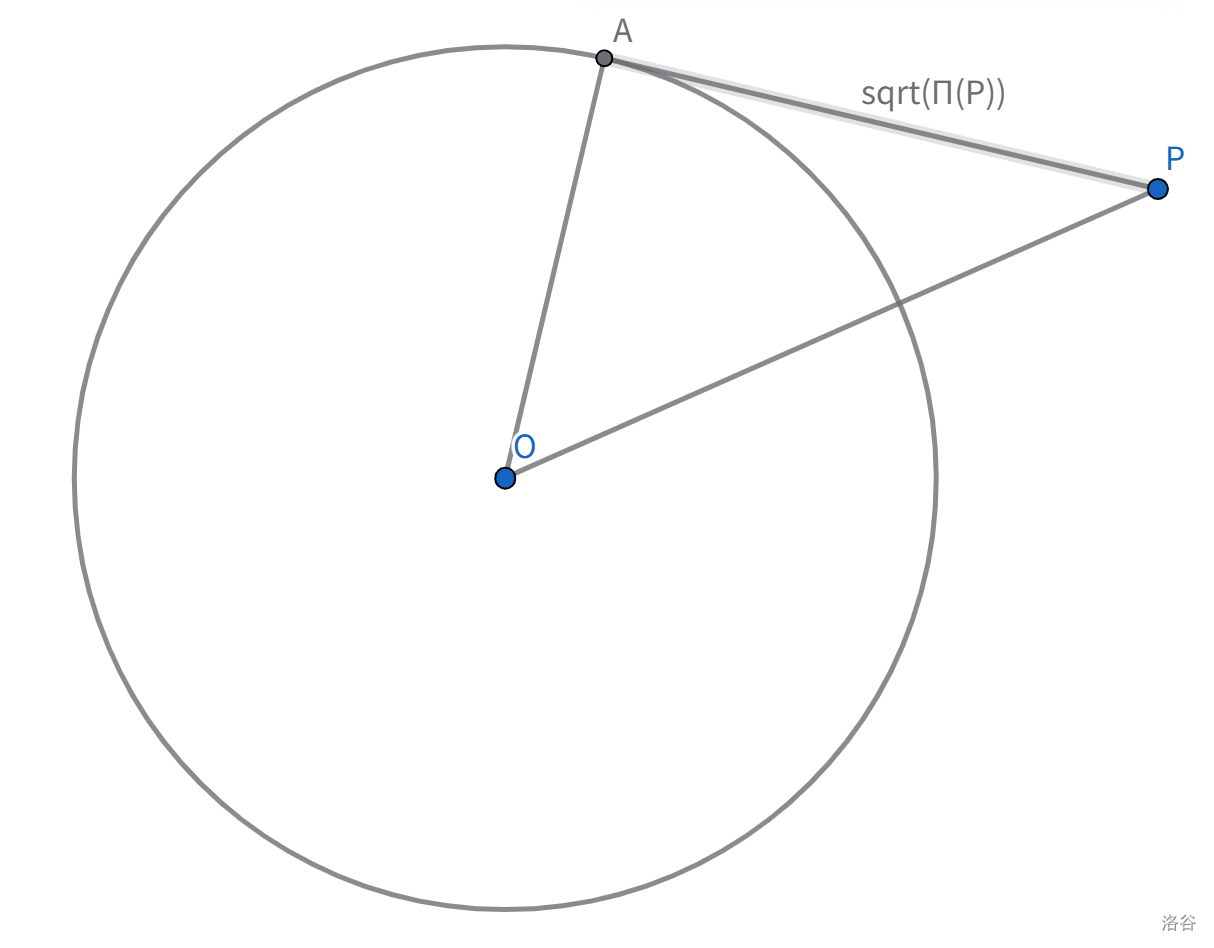
因此圆幂和切线相关的问题有很强的关联。
根轴
\[\begin{aligned} O_1 P^2 - r_1^2 &= O_2 P^2 - r_2^2 \\ O_1 P^2 - O_2 P^2 &= r_1^2 - r_2^2 \\ \end{aligned}\]有两个圆 $\Omega_1, \Omega_2$。探究满足 $\Pi_{\Omega_1}(P) = \Pi_{\Omega_2}(P)$ 的点 $P$ 的轨迹。
这个轨迹被称为根轴 (radical axis)。
问题转变为：求到两点距离平方差为定值的点的轨迹。
出现了很多平方，我们考虑使用勾股定理。过 $P$ 作一条垂线，垂足为 $H$：
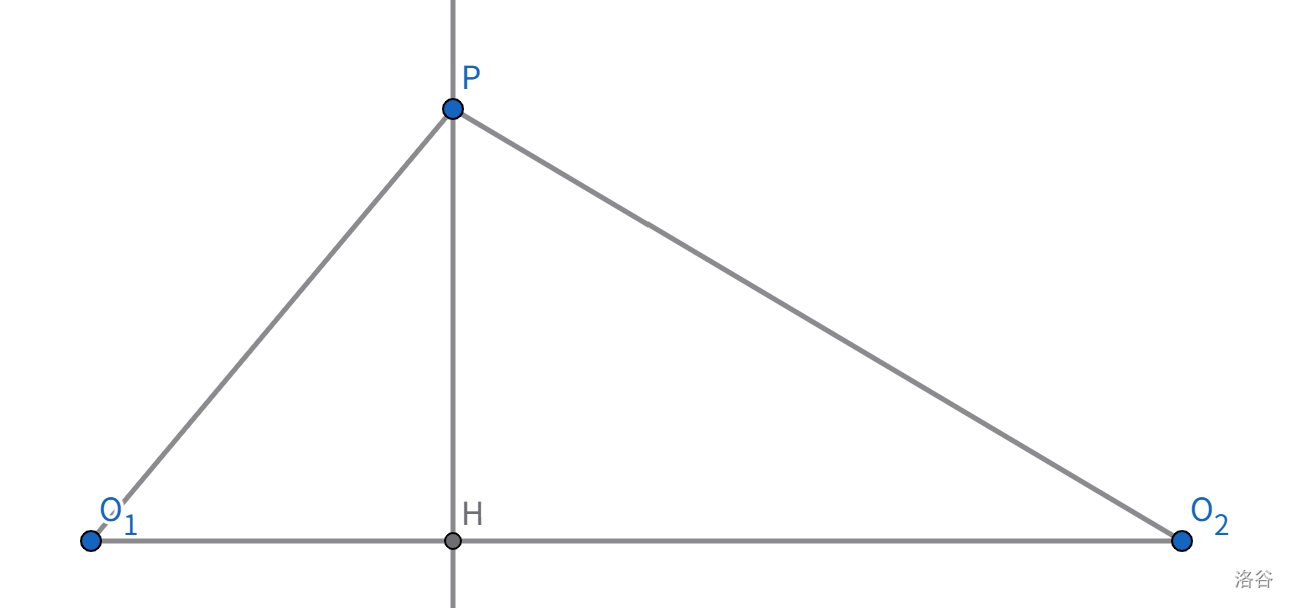
- $O_1 P^2 = PH^2 + O_1 H^2$
- $O_2 P^2 = PH^2 + O_2 H^2$
而同时 $O_1 H + H O_2$ 是定值，因此 $O_1 H, O_2 H$ 都被确定。即 $H$ 是定点，或者说 $P$ 在 $O_1 O_2$ 上的投影是定点。
反过来也不难证明，若 $P$ 在 $O_1 O_2$ 上的投影就是这个 $H$ 点，则 $P$ 就是满足条件的。
因此 $P$ 的轨迹是一条垂直于 $O_1 O_2$ 垂足为 $H$ 的直线。
相交圆的根轴
对于圆 $\Omega_1, \Omega_2$，已知它们交于 $A,B$ 两个不同点，它们的根轴有没有简单的表示？
注意到
\[\begin{cases} \Pi_{\Omega_1}(A) = \Pi_{\Omega_2}(A) = 0 \\ \Pi_{\Omega_1}(B) = \Pi_{\Omega_2}(B) = 0 \\ \end{cases}\]因此 $A,B$ 都在根轴上。由于根轴是直线，所以就是直线 $AB$。
结论：相交圆的根轴是公共弦所在直线。
相切圆的根轴
对于圆 $\Omega_1, \Omega_2$，已知它们切于 $A$，它们的根轴有没有简单的表示？
首先根据一样的原理，$A$ 在根轴上。又知根轴是一条垂直于 $O_1 O_2$ 的直线，因此就是垂直于 $O_1 O_2$ 的垂足为 $A$ 的直线。
省流：相切圆的根轴是垂直于连心线垂足为切点的直线。
感性理解：相交圆根轴的极限情况，即 $A,B$ 是同一个点。
根轴平分公切线段
对于圆 $\Omega_1, \Omega_2$，它们的根轴和公切线有什么关系？
首先我们知道：
- $P$ 到 $\Omega_1$ 的切线段长度为 $\sqrt {\Pi_{\Omega_1}(P)}$。
- $P$ 到 $\Omega_2$ 的切线段长度为 $\sqrt {\Pi_{\Omega_2}(P)}$。
而若 $P$ 在根轴上，则 $\Pi_{\Omega_1}(P) = \Pi_{\Omega_2}(P)$，因此两个切线段相等。
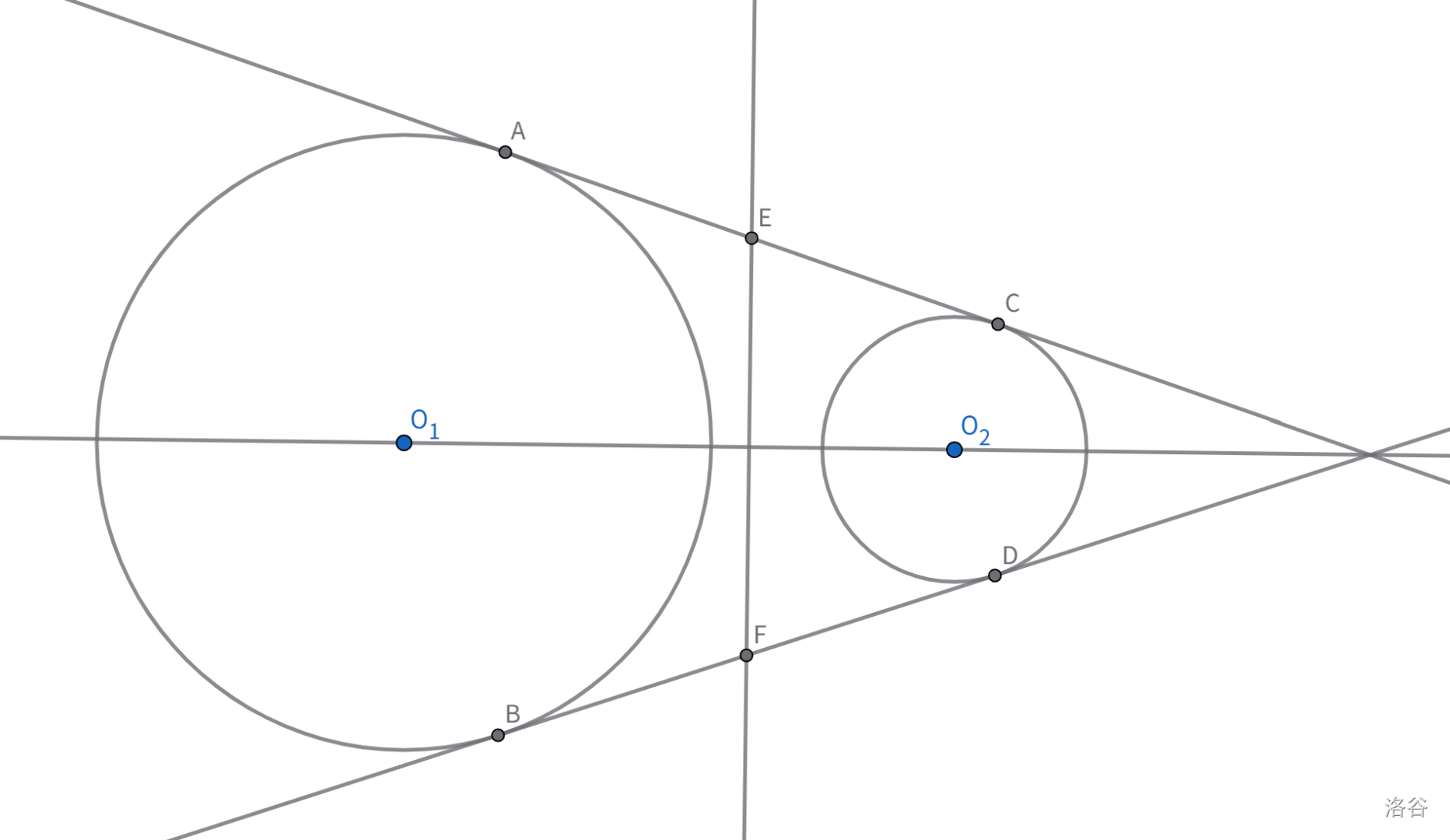
因此，两圆的根轴平分它们的每一条公切线段，无论是外公切线还是内公切线。
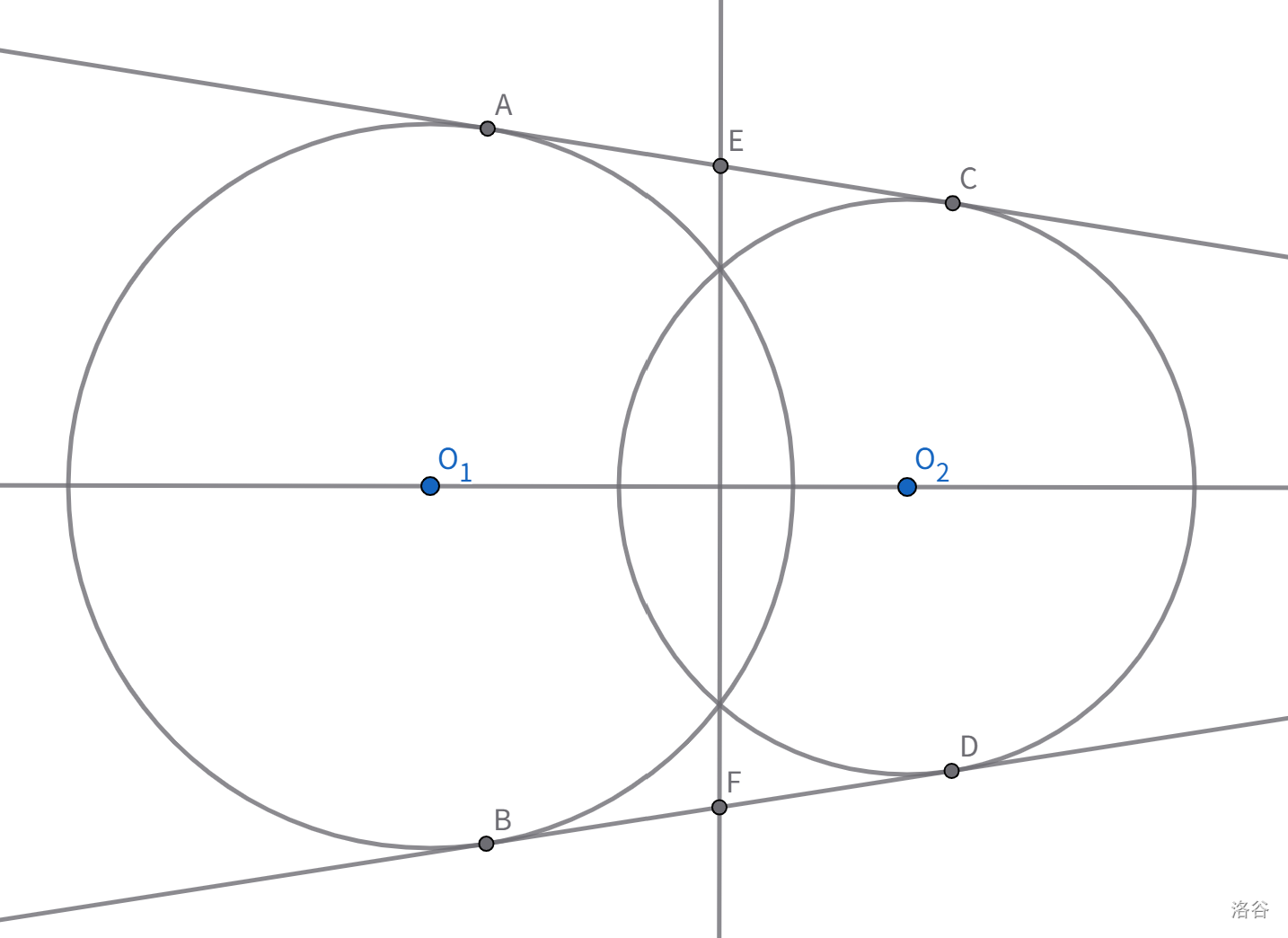
根心
有三个圆 $\Omega_1, \Omega_2, \Omega_3$。它们两两可以构成 $3$ 个根轴。这个图有什么性质？
但凡画一下这个图都会觉得三个根轴共点（图中的红点 $R$），这个共点称为根心 (radical center)。根心是比根轴更为特别的存在：根心处三个圆幂均相等。
这很容易证明：考虑根轴 $g_{1,2}$ 和 $g_{1,3}$ 的交点 $R$，这一点处：
\[\begin{cases} \Pi_{\Omega_1}(R) = \Pi_{\Omega_2}(R) \\ \Pi_{\Omega_1}(R) = \Pi_{\Omega_3}(R) \\ \end{cases}\]得到
\[\Pi_{\Omega_2}(R) = \Pi_{\Omega_3}(R)\]说明 $R$ 也在 $g_{2,3}$ 上，得证。
当然还有一个特殊情况，就是三条根轴平行，此时可以认为根心是无穷远点。
结论：三个圆形成的三条根轴要么共点要么平行。
图中的绿色圆是一个冷门知识点：以根心为圆心可以作出一个圆，使得这个圆和本来的三个圆都垂直，这个绿圆称为根圆 (radical circle)。