Andy AMC 课 12.21 作业
Published:
2005 AIME I #15 (Normal)
三角形 $ABC$ 的内切圆将中线 $AD$ 三等分。
已知 $BC=20$,求三角形面积。
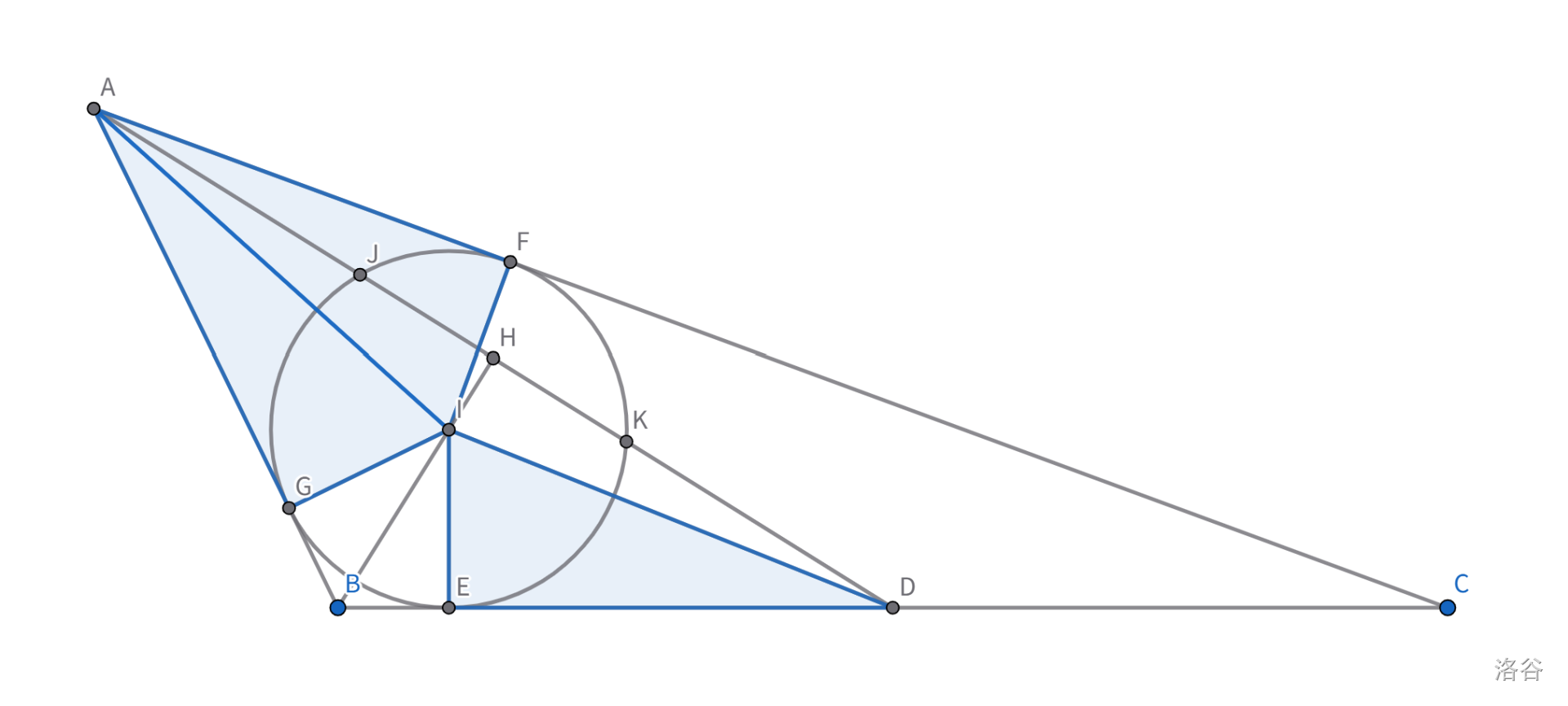
观察 1:三等分中线这个条件很奇怪。经过尝试,我们作 $IH \perp AD$,然后就能发现 $AI = DI$。
【这步没发现】观察 2:进一步地,$ABD$ 是一个等腰三角形,$AB=DB=10$。而且图里的 $3$ 个蓝色三角形全等。
【这步没发现】观察 3:切线怎么用?圆幂定理。
设中线总长为 $6k$,圆幂定理可以算出 $AF=AG = 2 \sqrt 2 k$。
然后可以导出 $AC = 10 + 4 \sqrt 2 k$。
此时使用中线长公式
\[AD^2 = \frac 1 2 (AB^2 + AC^2) - \frac 1 4 BC^2\] \[(6k)^2 = \frac 1 2 (10^2 + (10 + 4 \sqrt 2 k)^2) - \frac 1 4 20^2\]解得 $k = 2 \sqrt 2$,$AC = 26$。海伦公式算得面积 $\boxed{24 \sqrt {14}}$。
2016 AIME I #15 (Hard)
神题!
有两个圆 $\omega_1, \omega_2$ 交于 $X,Y$。作它们的一条公切线,切点为 $A,B$。
又有一个圆 $\omega_3$,它和 $\omega_1$ 交于 $D$,和 $\omega_2$ 交于 $C$。$D,Y,C$ 恰好三点共线。
已知 $XC = 67, XD = 37$ 以及 $XY = 47$。
求 $AB^2$。
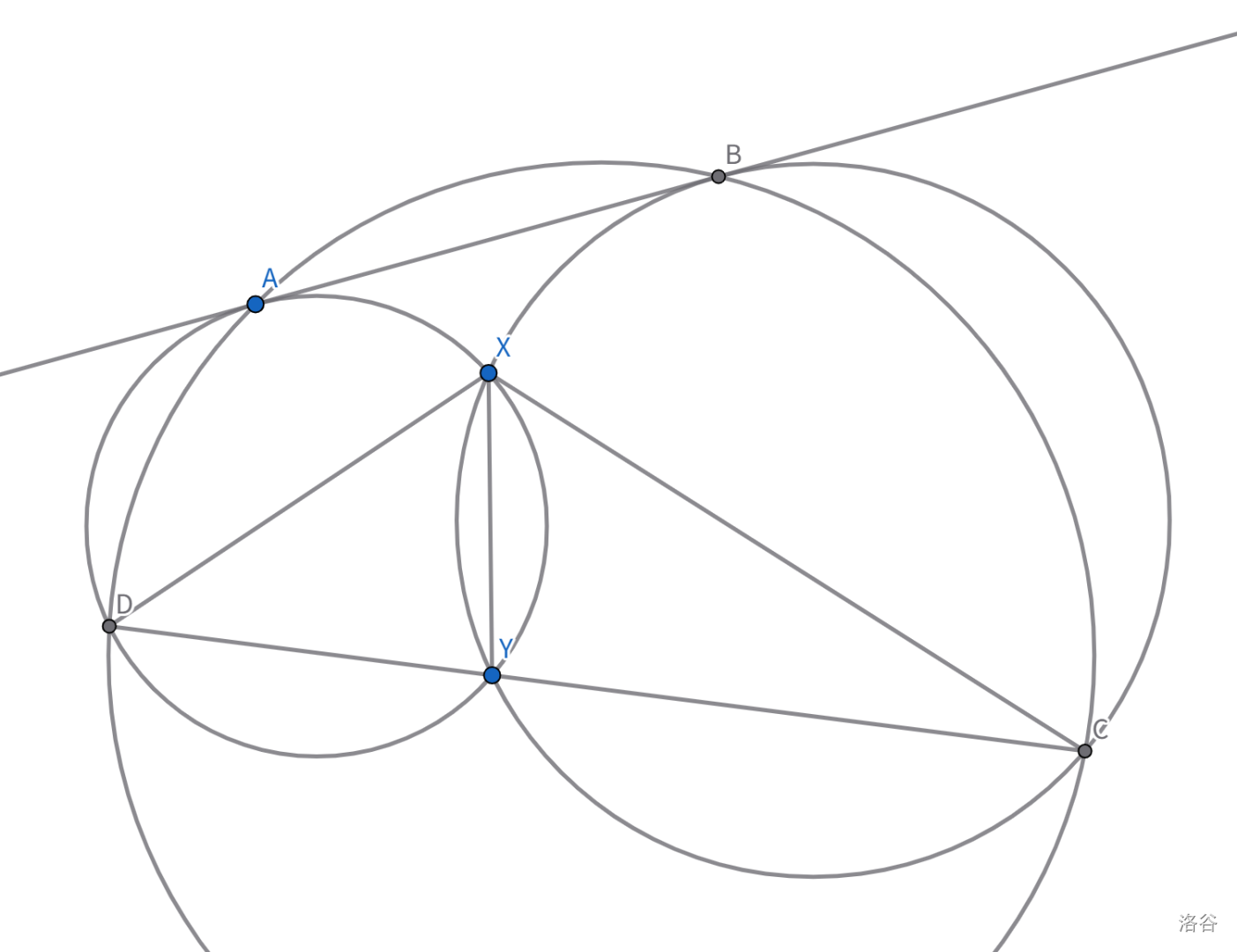
观察 1:相交圆公切线,辅助线肯定要作它们的公共弦(根轴),延长公共弦与公切线交于 $Z$,有经典结论 $AZ=BZ$。
观察 2:三个圆的三个根轴交于根心,所以我们延长 $DA, CB, YX$,三线共点交于根心 $P$。
【这步没发现】观察 3:对三角形 $CDP$ 使用 Miquel 定理,得到 $AXBP$ 四点共圆。
【这步没发现】观察 4:对于圆 $AXBP$ 使用圆幂定理,$AZ^2 = ZX \times ZP$。同时我们前面在观察 1 的经典结论中已经知道了 $AZ^2 = ZX \times ZY$,可得 $ZP = ZY$。
【这步没发现】观察 5:由 $ZP=ZY$ 且 $ZA=ZB$ 可得 $AYBP$ 是平行四边形。四点共圆导出相似 $\triangle DXP \sim \triangle PXC$。算出 $PX = \sqrt{37 \times 67}$。
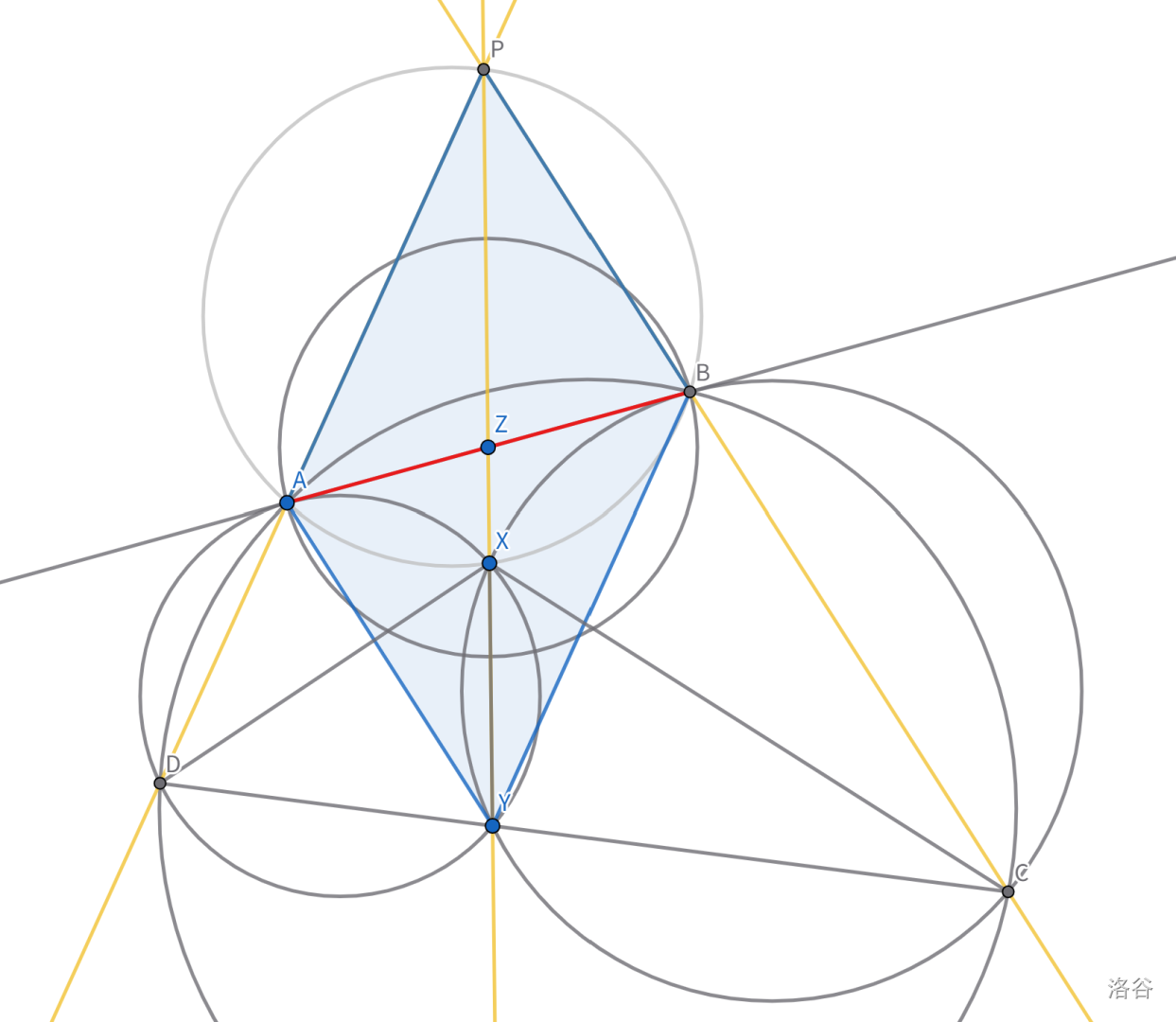
此时 $PY$ 上的所有边都能算了。最后可以得到 $AB^2 = 37 \times 67 - 47^2 = \boxed{270}$。
2020 AIME I #15 (Hard)
有一三角形 $ABC$,其垂心为 $H$,外接圆为 $\omega$。作三角形 $BHC$ 的外接圆 $\omega’$,过 $H$ 作 $\omega’$ 的切线,与 $\omega$ 交于 $X,Y$。
已知 $HA=3, HX=2, HY=6$,求三角形 $ABC$ 面积。
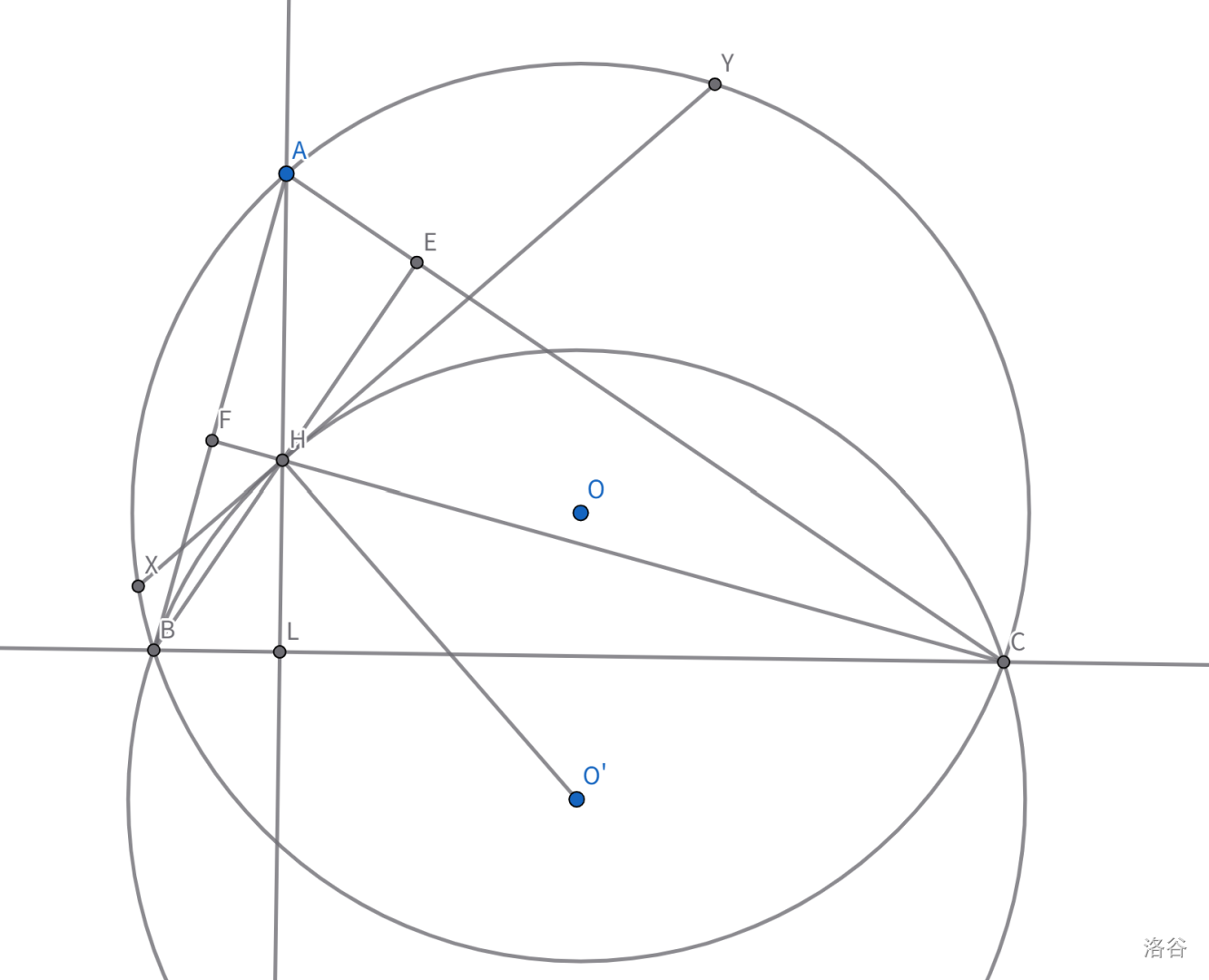
观察 1:这个如同空中楼阁一般的 $XY$ 很容易想到圆幂。延长 $AH$ 与外接圆交于 $H’$,可以算出 $HH’ = 4$。
观察 2:导角可以发现三角形 $BHC$ 与 $BH’C$ 全等。辅助线作 $BH’$ 和 $CH’$ 显然是好的。$\omega’$ 是三角形 $BH’C$ 的外接圆,这意味着这两个圆等大。而且整张图中 $BC$ 像一面镜子一样。
【这步没发现】观察 3:等大的圆,不仅可以理解为轴对称,还可以理解为平移。$A \to H$ 的平移和 $O \to O’$ 是一样的,因此 $AHO’O$ 是平行四边形。辅助线作 $AO$ 和 $OO’$ 显然是好的。然后可以立刻得到 $AO$ 与 $XY$ 垂直,甚至形成了垂径。
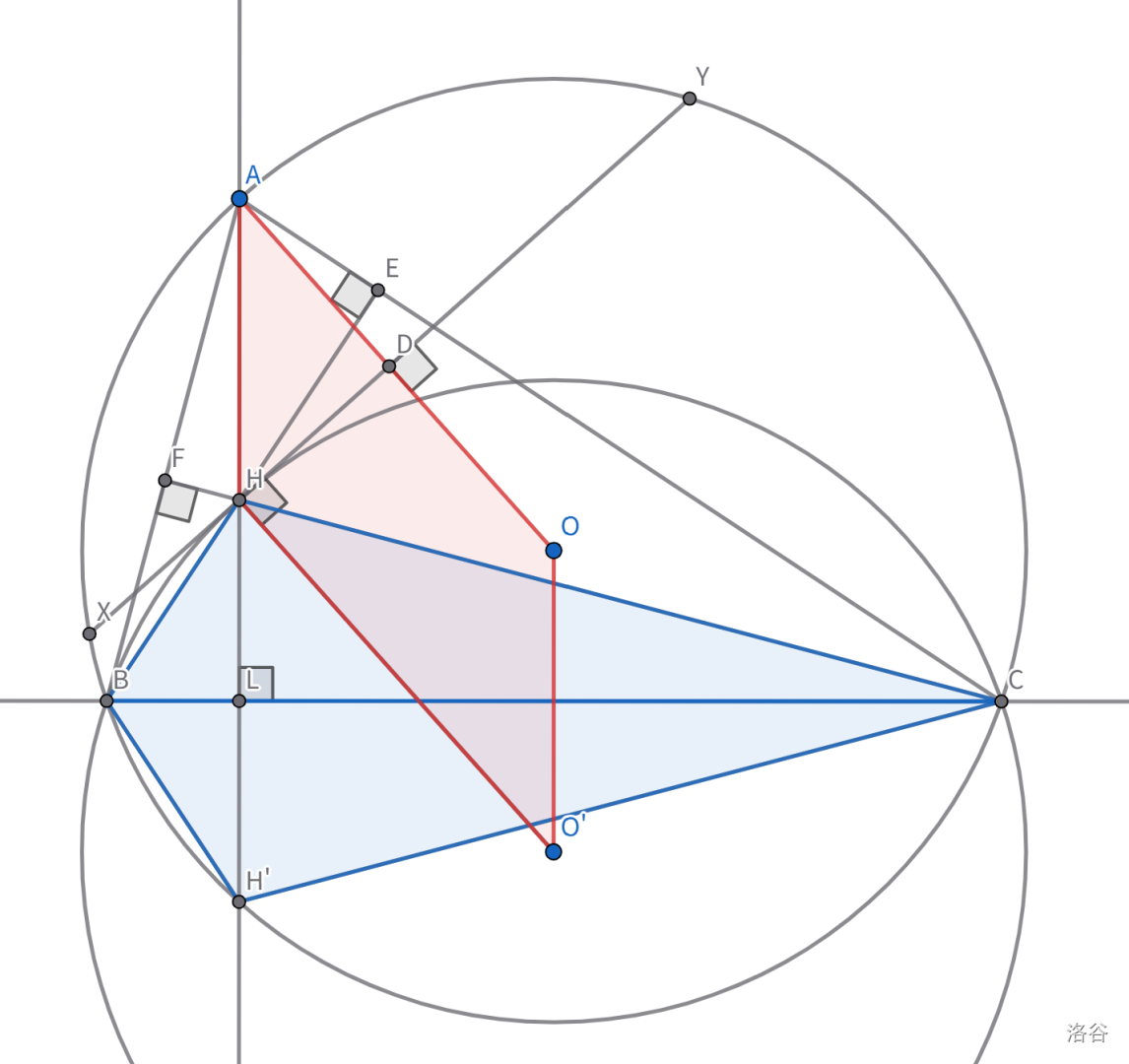
做到这已经够了。$AD = \sqrt{AH^2 - DH^2} = \sqrt 5$。
$OY^2 - DY^2 = OD^2$,即 $r^2 - 4^2 = (r - \sqrt 5)^2$,解得 $r = \frac {21} {10} \sqrt 5$。
\[BC = 2 \sqrt{r^2 - (\frac 3 2)^2} = \frac 6 5 \sqrt{55}\] \[A = \frac 1 2 BC \times AL = \frac 1 2 \times \frac 6 5 \sqrt{55} \times 5 = \boxed{3 \sqrt{55}}\]2023 AIME II #13 (Normal)
大致思路对了,但没做出来。
锐角 $A$ 满足 $\tan A = 2 \cos A$。求有几个 $1000$ 以内的正整数 $n$,使得 $\tan^n A + \sec^n A$ 是一个个位为 $9$ 的整数。
观察 1:$a^n + b^n$ 形式,还有数论,那肯定是牛顿和做递推。令 $S_n = a^n + b^n$:
\[S_n = (a + b) S_{n-1} - ab S_{n-2}\]观察 2:三角函数显然是个幌子。因为可以简单转化
\[\tan A = 2 \cos A \iff \tan A \sec A = 2\] \[\begin{cases} \tan A \sec A = 2 \\ \sec^2 A - \tan^2 A = 1 \\ \end{cases}\]此时三角函数已经没用。设 $a = \sec A \in [1, \infty), b = \tan A \in [0, \infty)$,则:
\[\begin{cases} ab = 2 \\ a^2 - b^2 = 1 \\ \end{cases}\]尝试解一下发现 $a,b$ 不简单。但是注意一下会发现 $a^2, b^2$ 是简单的:
\[\begin{cases} a^2 = \frac {\sqrt {17} + 1} 2 \\ b^2 = \frac {\sqrt {17} - 1} 2 \\ \end{cases}\]我们盲猜一波只有 $2 \mid n$ 是合法的。设 $\alpha = a^2, \beta = b^2$,设 $S_n = \alpha^n + \beta^n$。
\[S_n = (\alpha + \beta) S_{n-1} - \alpha \beta S_{n-2}\] \[S_n = \sqrt{17} S_{n-1} - 4 S_{n-2}\]好像……还是不太对?手玩一下会发现只有偶数项是整数,奇数项全是几倍 $\sqrt{17}$ 的形式。
那我们推导重来,这次我们知道了,在 $2 \mid n$ 时只有 $4 \mid n$ 是合法的。重新设 $\alpha = a^4 = \frac {9 + \sqrt {17}} 2, \beta = b^4 = \frac {9 - \sqrt {17}} 2$,设 $S_n = \alpha^n + \beta^n$。
\[S_n = (\alpha + \beta) S_{n-1} - \alpha \beta S_{n-2}\] \[S_n = 9 S_{n-1} - 16 S_{n-2}\]这下舒服了。加上边界条件写得完整一点:
\[a^{4n} + b^{4n} = S_n = \begin{cases} 2 & n = 0 \\ 9 & n = 1 \\ 9 S_{n-1} - 16 S_{n-2} & n \ge 2 \\ \end{cases}\]在 $\bmod 10$ 下计算,并信仰其循环节很短:算出除了 $n=0$ 是 $2$ 以外,其余项遵循长度为 $3$ 的循环节 $\langle 9,9,7 \rangle$。
我们得到了题目要求的充分条件:
- 对于正整数 $n$,$\tan^n A + \sec^n A$ 是整数,当且仅当 $4 \mid n$。
- 对于正整数 $n$,$\tan^n A + \sec^n A$ 是个位为 $9$ 的整数,当且仅当 $4 \mid n$ 且 $3 \nmid \frac n 4$(即 $12 \nmid n$)。
事实上可以说明这是充要条件。刚才漏掉的 $2 \nmid n$ 情况,考虑 $n=1$ 肯定不对,更大的奇数满足递推,但是只是 $\sqrt {17}$ 也不足以让根号里那一坨出来。总之这一块直觉上很对,写起来可能有点 dirty。
因此答案为
\[\lfloor \frac {1000} 4 \rfloor - \lfloor \frac {1000} {12} \rfloor = \boxed{167}\]HMMT 2025 Feb AN #7 (Easy)
该比赛答案文件链接。
独立做对了!花了 8min。
官方做复杂了,我的做法比官方简单多了。
\[\begin{cases} 2 (a^2 + 1) = 3 (b^2 + 1) = 4 (c^2 + 1) \\ ab + ac + bc = 1 \\ a, b, c > 0 \\ \end{cases}\]求 $a + b + c$。
齐次化。
\[\begin{aligned} & a^2 + 1 \\ =& a^2 + (ab + ac + bc) \\ =& (a + b) (a + c) \\ \end{aligned}\]用一样的手法处理:
\[2 (a+b) (a+c) = 3 (a+b) (b+c) = 4 (a+c) (b+c)\] \[\frac 2 {b+c} = \frac 3 {a+c} = \frac 4 {a+b}\]可以解出 $a![]() c = 5:3:1$。最终答案 $\boxed{\frac 9 {23} \sqrt{23}}$。
c = 5:3:1$。最终答案 $\boxed{\frac 9 {23} \sqrt{23}}$。
2002 AIME I #12 (Ad-hoc, Easy)
何意味?
定义
\[f(z) = \frac {z + i} {z - i}\]求出 $f^{(2002)}(\frac 1 {137} + i)$ 的实部与虚部之和。这个符号代表函数迭代。
手玩注意到 $f^{(3)}(z) = z$,做完了。迭代出来是 $1 + 274 i$,答案 $\boxed{275}$。
一个算起来快一点的方法是把 Mobius 变换当矩阵乘法算,但是本质不变。
ChatGPT 指出,Mobius 变换有循环,当且仅当其对应矩阵的特征值之比为单位根,是几次单位根则循环节就是几。但是考场上当你算出特征值之比的时候别人这题都算完了。
2005 AIME II #15 (Easy)
做出来了,但我的方法有点烦。
已知
- 圆 $w_1$ 方程为 $(x+5)^2 + (y-12)^2 = 16^2$。
- 圆 $w_2$ 方程为 $(x-5)^2 + (y-12)^2 = 4^2$。
圆 $w_3$ 与 $w_1$ 内切,与 $w_2$ 外切。$w_3$ 的圆心在直线 $y=ax$ 上,$a>0$。
求 $a$ 的最小值的平方。
设 $O_1, O_2, O_3$ 为 $w_1, w_2, w_3$。
首先我们求 $O_3$ 的轨迹,直觉上这是一个椭圆。
设 $O_3$ 的半径为 $r$,$O_1 O_3 = 16-r$,$O_2 O_3 = 4+r$。注意 $O_1 O_3 + O_2 O_3 = 20$ 为定值,是椭圆。不难求得轨迹方程
\[\frac {x^2} {10^2} + \frac {(y-12)^2} {(5 \sqrt 3)^2} = 1\]官方解法
把 $y=ax$ 代入,切线意味着这个二次方程 $\Delta = 0$。
\[\frac {x^2} {10^2} + \frac {(ax-12)^2} {(5 \sqrt 3)^2} = 1\] \[\Delta = (\frac {24 a} {75})^2 - 4 (\frac 1 {100} + \frac {a^2} {75}) (\frac {144} {75} - 1) = 0\] \[a^2 = \boxed{\frac {69} {100}}\]我的解法
这个方法有局限,对于 $x_c \ne 0$ 可能没那么方便。
对于中心在 $(x_c, y_c)$ 的椭圆,其 $(x_0, y_0)$ 处切线方程为:
\[\frac {(x_0 - x_c)} {a^2} (x - x_c) + \frac {(y_0 - y_c)} {b^2} (y - y_c) = 1\]代入 $(x_c, y_c) = (0, 12)$,$(x, y) = (0, 0)$,可解出
\[y_0 = \frac {23} 4\]代回原本的椭圆方程可以解出
\[x_0^2 = \frac {575} {12}\] \[a^2 = \frac {y_0^2} {x_0^2} = \boxed{\frac {69} {100}}\]2022 AIME II #12 (Easy)
$a,b,x,y \in \mathbb R$,$a>4$ 且 $b>1$。已知
\[\frac {x^2} {a^2} + \frac {y^2} {a^2 - 16} = 1\] \[\frac {(x-20)^2} {b^2 - 1} + \frac {(y-11)^2} {b^2} = 1\]求 $a+b$ 最小值。
首先这个题一眼椭圆,数形结合。
【这步没发现】观察:半长轴平方 $a^2$,半短轴平方 $a^2 - 16$ 怎么用?其实说的是焦点到中心的距离为 $\sqrt{16} = 4$。
所以我们可以算出所有的焦点了:
- 椭圆 1:$A(-4, 0), B(4, 0)$
- 椭圆 2:$C(20, 10), D(20, 12)$
考虑怎么用 $a+b$ 最小这个条件。令 $(x,y)$ 这个两个椭圆的公共点为 $P$。
\[a+b = \frac {2a + 2b} 2 = \frac {AP + BP + CP + DP} 2\]因此 $P$ 其实是四边形 $ABCD$ 的费马点。有结论:凸四边形费马点为对角线交点。因此可以算出 $P(14, \frac {15} 2)$。
做完了,$a=13, b=10$,答案为 $\boxed{23}$。