高二上期末物理
Published:
电容器
电容器:能存储电荷和电能的装置
平行板电容器:
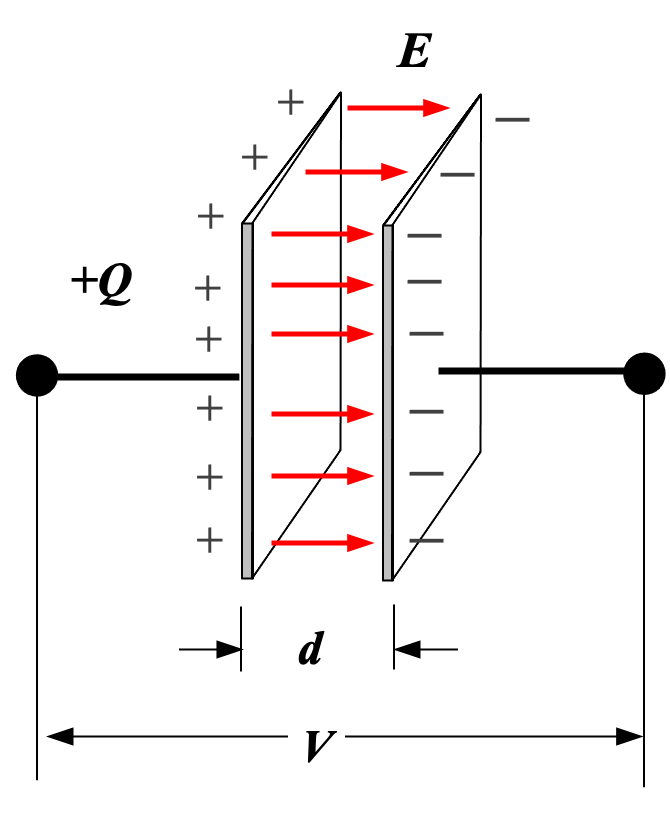
两极板当中可以是真空,也可以夹一层绝缘物质——电介质。
串联电源、电阻、电容器,两极板间会因为电势差逐渐积累等大的异号电荷,直到(无穷长时间后)两板间电势差增大到与电源两端电压相等时,充电过程完成。相反过程称为放电。
对于同一个电容器,$\frac Q U$ 是一个定值(实验定律)。定义这个比值为 $C$,称为该电容器的电容:
\[\boxed{ C := \frac Q U }\]单位是库仑每伏特(法拉,$F$)。普通的电容器的电容一般在 $\mu F$,$nF$,$pF$ 级别。
电压超过某个极限值(击穿电压)时,电介质会变为导体,称为电介质的击穿,导致电容器损坏。电容器的额定电压低于击穿电压。
【背诵】静电的利用与防范
- 利用
- 静电除尘
- 静电喷雾
- 静电复印
- 防范
- 良好接地
- 工艺控制
- 使用避雷针
电路
【背诵】电路绘制
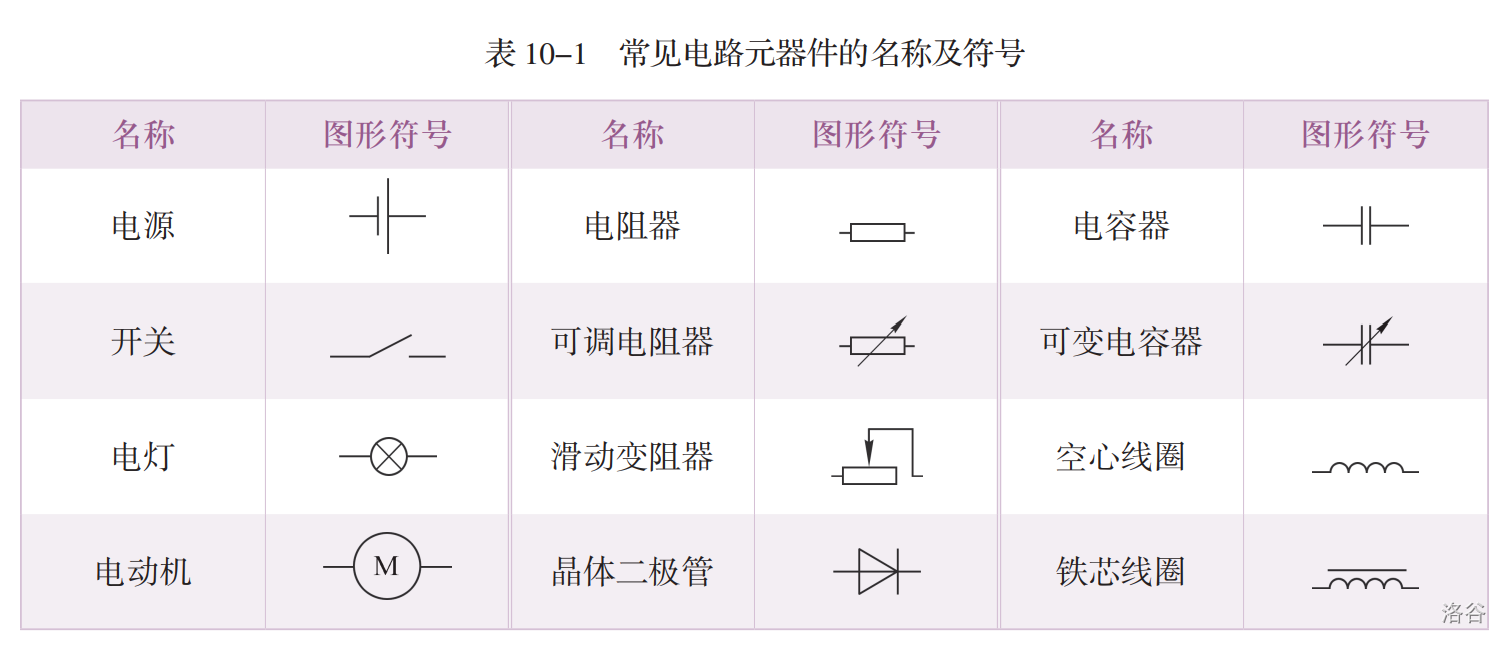
- 开关不用写圆圈了。
- 可调元件,写一个斜箭头。
- 空心线圈画成电感器,铁芯线圈在上面加一条杠。
电流的建模
- 导体中有两种东西:
- 自由电子:金属导体内的自由电荷。
- 原子实:失去电子的原子,“固定”在晶体结构点阵上。
- 自由电子以很高的速率(约 $10^5$ 米每秒)做无规则热运动,宏观上看不形成电流。
- 当施加电场时,自由电子获得与电场方向相反的加速度,但是由于和原子实碰撞因此无法无限加速。最终在宏观上平均出一个与电场方向相反的速度,称为漂移速度。
- 漂移速度非常小,可能比蜗牛慢。
- 由于漂移速度的存在,整体上电子发生了与电场方向相反的移动,电流就产生了。
电流
通过导体某一横截面的电荷量 $Q$ 与所用时间 $t$ 之比称为电流:
\[\boxed{ I := \frac Q t }\]电阻定律
导体的电阻 $R$ 和啥有关?
电阻定律:根据实验,
- 在温度不变时,
- 与导体的长度 $L$ 成正比,
- 与导体的横截面积 $S$ 成反比,
- 与构成它的材料有关。
比例系数 $\rho$ 称为电阻率,单位为欧姆乘米。温度不变时,同种材料 $\rho$ 相同。
测量圆形金属丝的电阻率
\[\rho = \frac {\pi d^2 R} {4 L}\]直径可以用游标卡尺测量。
内阻
电源内部也有电阻。
- 闭合电路:由电源、用电器和导线等组成的完整回路。分为两部分:
- 外电路:电源外部的电路(我们熟悉的部分)。
- 外电阻 $R$:外电路对电流的阻碍作用,即外电路的电阻。
- 外电压 / 端电压 $U_外$:外电路两端的电压,电源正负极两端的电压(我们熟悉的电源电压)。
- 内电路:电源内部的电路。
- 内电阻 $r$:内电路对电流的阻碍作用,即内电路的电阻。
- 内电压 $U_内$:内电路两端的电压。
内外电压之和为恒量,称为电源电动势 $E$:
\[\boxed{ E := U_内 + U_外 }\]闭合电路欧姆定律
由电源电动势和部分电路欧姆定律可得:
\[\begin{cases} E := U_内 + U_外 \\ U_外 = IR \\ U_内 = Ir \\ \end{cases}\]得
\[\boxed{ I = \frac E {R + r} }\]这个结论称为闭合电路欧姆定律。
电压与电动势
在电源内部,正极电势高于负极,当自由电子从负极出发到达正极时静电力会阻碍它从电源内部回负极。也就是说,必须要有非静电力帮它。这可能是化学作用,也可能是电磁作用等。
因此我们得到了电压和电动势的关键区别:
- 电压——静电力做功,由电能转化为其它形式的能量
- 电动势——非静电力做功,由其它形式的能量转化为电能
电池组
我现在有 $n$ 个电动势为 $E$ 内阻为 $r$ 的电池。
串联
\[\boxed{\begin{cases} E_串 = nE \\ r_串 = nr \\ \end{cases}}\]并联
\[\boxed{\begin{cases} E_并 = E \\ r_并 = \frac r n \\ \end{cases}}\]电功
对于一段导体
\[\begin{cases} W = qU \\ q = It \\ \end{cases}\]我们可知电场力对电子做的功为
\[\boxed{ W = UIt }\]单位为焦耳。生活中的常见单位还有千瓦时。
根据电功率的定义
\[\boxed{ P := \frac W t }\]得
\[\boxed{ P = UI }\]单位为瓦特。
电热
纯电阻电路:电路将消耗的电能全部用于发热。
即热量 $Q$ 满足
\[\boxed{ Q = W }\]根据 $W = UIt$ 和 $U = IR$,可知 $Q = I^2 R t$。
这个结论对纯电阻电路成立是显然的。但是,在非纯电阻电路中,这个结论居然也成立(属于实验定律)。
这被称为焦耳定律:电流通过导体产生的热量 $Q$,与电流 $I$ 的二次方、导体的电阻 $R$ 和通电的时间 $t$ 成正比。
\[\boxed{ Q = I^2 R t }\]在非纯电阻电路中,$W - Q$ 即为电能转化为除了内能以外的能的部分,常见的比如说动能。
\[\begin{aligned} W &= Q + W_{\text{other}} \\ UIt &= I^2 R t + W_{\text{other}} \\ \end{aligned}\]同时除以 $t$ 得
\[UI = I^2 R + P_{\text{other}}\]辨析!
- $P = \frac W t$:功率的定义式,啥情况都能用。
- $P = UI$:适用于电功率的计算式。
- $P = I^2 R$:适用于电阻发热功率的计算,只能算电路中产生的内能,不包括其他的能。
- $P = \frac {U^2} R$:适用于纯电阻电路发热功率的计算式。
- 欧姆定律的适用范围为纯电阻电路。$I^2 R$ 变 $\frac {U^2} R$ 的过程中用到了 $I = \frac U R$。
- $P = Fv$:?
- 机械功率的瞬时表达式。
- 严谨的话应该是 $P = \vec F \cdot \vec v$。所以只适用于 $\vec F$ 与 $\vec v$ 共线的情况。
- 推导方法:$dW = \vec F \cdot d\vec r$,同时对 $t$ 求导。
例题
有一电动自行车:
- 额定输出功率 $250$ 瓦
- 额定工作电流 $12$ 安
- 额定工作电压 $48$ 伏
问:
- 该电动自行车电动机的电阻阻值为多少?
- 正常工作时效率为多少?效率用符号 $\eta$ 表示。
- 该电动自行车的标称最大速度为 $25$ 千米每时,若不考虑其他影响因素,电动自行车所受到的阻力为多少?
第一问:
错解:
\[R \ne \frac U I = 4 \ce{ \Omega}\](欧姆定律不适用!)
正解:
\[\begin{aligned} UI &= I^2 R + P_出 \\ R &= \frac {UI - P_出} {I^2} = \boxed{\frac {163} {72} \ce{ \Omega}} \\ \end{aligned}\]第二问:
\[\begin{aligned} \eta &= \frac {P_出} {P_入} \times 100\% \\ &= \frac {P_出} {UI} \times 100\% \\ &= \boxed{\frac {125} {288}} \\ &\approx 43.4\% \\ \end{aligned}\]第三问:
\[f = F = \frac {P_出} v = \boxed{36 \ce{ N}}\]