Tongrui 5.1 三角函数
Published:
总结
- 三角函数公式推导
- Euler 公式是核心。
- 和差角公式通过 $e^{i(x+y)} = e^{ix} e^{iy}$ 得到。
- 积化和差通过直接展开后分组得到。
- 和差化积通过构造因式分解得到。
- 熟悉 $\cos(n \theta)$ 和 $\sin(n \theta)$ 的 Chebyshev 多项式性质。
- 熟悉 $2 \sin(n \theta)$ 的乘积展开。
- 三角函数连乘——构造复数模长 / 使用 $\sin$ 的乘积展开。
- 三角函数迭代——分析增减性。很多三角函数函数迭代的题中三角函数都是假的,它只是为了提供一个确定的极值和一个奇怪的增减性而已。
三角函数
平方式
\[\sin^2 x + \cos^2 x = 1\]同时除以 $\cos^2 x$ 得到变种:
\[\tan^2 x + 1 = \sec^2 x\]同时除以 $\sin^2 x$ 得到变种:
\[1 + \cot^2 x = \csc^2 x\]Euler 公式
\[e^{ix} = \cos x + i \sin x\] \[\sin x = \frac {e^{ix} - e^{-ix}} {2i}\] \[\cos x = \frac {e^{ix} + e^{-ix}} 2\]和角公式
\[e^{i(x+y)} = e^{ix} e^{iy}\]同时取实部:
\[\cos(x+y) = \cos x \cos y - \sin x \sin y\]同时取虚部:
\[\sin(x+y) = \sin x \cos y + \cos x \sin y\]两者相除:
\[\tan(x+y) = \frac {\tan x + \tan y} {1 - \tan x \tan y}\]积化和差
\[\begin{aligned} \cos x \cos y &= \frac 1 2 \frac {(e^{ix} + e^{-ix}) (e^{iy} + e^{-iy})} 2 \\ &= \frac 1 2 \left( \frac {e^{i(x+y)} + e^{-i(x+y)}} 2 + \frac {e^{i(x-y)} + e^{-i(x-y)}} 2 \right) \\ &= \frac 1 2 (\cos(x+y) + \cos(x-y)) \end{aligned}\]同理:
- $\sin x \sin y = - \frac 1 2 (\cos(x+y) - \cos(x-y))$
- $\sin x \cos y = \frac 1 2 (\sin(x+y) + \sin(x-y))$
- $\cos x \sin y = \frac 1 2 (\sin(x+y) - \sin(x-y))$
和差化积
直接 Euler 公式后因式分解:
\[\begin{aligned} & \cos x + \cos y \\ =& \frac 1 2 (e^{ix} + e^{-ix} + e^{iy} + e^{-iy}) \\ =& \frac 1 2 (e^{i \frac {x+y} 2} + e^{-i \frac {x+y} 2}) (e^{i \frac {x-y} 2} + e^{-i \frac {x-y} 2}) \\ =& 2 \cos \frac {x+y} 2 \cos \frac {x-y} 2 \\ \end{aligned}\]同理:
- $\cos x - \cos y = -2 \sin \frac {x+y} 2 \sin \frac {x-y} 2$
- $\sin x + \sin y = 2 \sin \frac {x+y} 2 \cos \frac {x-y} 2$
- $\sin x - \sin y = 2 \cos \frac {x+y} 2 \sin \frac {x-y} 2$
可以理解为从积化和差公式调整 $x+y$ 和 $x-y$。
倍角
- 第一类 Chebyshev 多项式:$\cos(n \theta)$ 总是关于 $\cos \theta$ 的 $n$ 次多项式。
- 第二类 Chebyshev 多项式:$\frac {\sin(n \theta)} {\sin \theta}$ 总是关于 $\cos \theta$ 的 $n-1$ 次多项式。
令 $z_n = \cos(n \theta) + i \sin(n \theta) = e^{i n \theta}$。考虑把 $z_n$ 同时往前后转一格:
\[\begin{aligned} (e^{i \theta} + e^{-i \theta}) z_n &= e^{i \theta} z_n + e^{-i \theta} z_n \\ 2 \cos \theta z_n &= z_{n+1} + z_{n-1} \\ \end{aligned}\]下标移一位:
\[\boxed{z_n = 2 \cos \theta z_{n-1} - z_{n-2}}\]实部虚部拆开,会发现 $\cos(n \theta)$ 和 $\sin(n \theta)$ 满足一样的二阶线性递推:
\[\boxed{\begin{cases} \cos(n \theta) = 2 \cos \theta \cos((n-1) \theta) + \cos((n-2) \theta) \\ \sin(n \theta) = 2 \cos \theta \sin((n-1) \theta) + \sin((n-2) \theta) \\ \end{cases}}\]这个可以被出成很阴间的 Ad-hoc 题,如 5.5 章的 Example 5.26。
二倍角
\[\sin 2x = 2 \sin x \cos x\] \[\cos 2x = \begin{cases} \cos^2 x - \sin^2 x \\ 2 \cos^2 x - 1 \\ 1 - 2 \sin^2 x \\ \end{cases}\] \[\tan 2x = \frac {2 \tan x} {1 - \tan^2 x}\]$\sin^2, \cos^2$ 也是正弦波,频率是原来的两倍:
\[\sin^2 x = \frac {1 - \cos 2x} 2\] \[\cos^2 x = \frac {1 + \cos 2x} 2\]三倍角
\[\sin 3x = -4 \sin^3 x + 3 \sin x\] \[\cos 3x = 4 \cos^3 x - 3 \cos x\]做题时,看到 $4:3$ 的系数就要警惕了。
万能公式
令 $t = \tan \frac x 2$,有
\[\tan x = \frac {2t} {1 - t^2}\] \[\sin x = \frac {2t} {1 + t^2}\] \[\cos x = \frac {1 - t^2} {1 + t^2}\]$\sin$ 和 $\cos$ 的模长公式
来自 Example 5.2。
\[\lvert \sin x \rvert = \frac 1 2 \lvert e^{2ix} - 1 \rvert\] \[\lvert \cos x \rvert = \frac 1 2 \lvert e^{2ix} + 1 \rvert\]对三角函数乘积的题目比较有用。
几何意义是单位圆上的弦长。
$\sin$ 的 $n$ 倍角乘积公式
来自 Example 5.2。
\[\prod_{k=0}^{n-1} 2 \sin \left( z + \frac k n \pi \right) = 2 \sin (nz)\]形式很像取整函数的 Hermite 恒等式,可以看作是 $2 \sin$ 这个函数的“Hermite 恒等式”。
三角求和
\[\sum_{k=1}^n \sin k = \frac {\sin \frac n 2 \sin \frac {n+1} 2} {\sin \frac 1 2}\] \[\sum_{k=1}^n \cos k = \frac {\sin \frac n 2 \cos \frac {n+1} 2} {\sin \frac 1 2}\]Example 5.2 AIME I 2025 #13 (Hard)
求出
\[\prod_{k=1}^{45} \csc^2 (2k-1)° = \frac 1 {\sin^2 1°} \times \frac 1 {\sin^2 3°} \times \cdots \times \frac 1 {\sin^2 89°}\]
定求积问题,考虑首尾配对,但是这个配完之后要算 $\sin 2° \sin 6° \cdots$,反倒更难了。
那还有什么方法可以处理 $\sin$ 的乘积?
- Sol 1:$\sin$ 和复数有关,如果能把它写成某个复数的模长,那模长对乘积就是友好的。
- Sol 2:$\sin$ 不是有自己的乘积公式吗?
Sol 1
\[\begin{aligned} \sin x &= \frac {e^{ix} - e^{-ix}} {2i} \\ \sin x &= \frac 1 2 \frac {e^{2ix} - 1} {i e^{ix}} \\ \lvert \sin x \rvert &= \frac 1 2 \lvert e^{2ix} - 1 \rvert \end{aligned}\] \[\sin (2k-1)° = \sin \frac {(2k-1) \pi} {180} = \lvert \omega_{180}^{2k-1} - 1 \rvert\]成功表示了,然后考虑 $\prod (\omega_{180}^{2k-1} - 1)$ 怎么求。熟知与奇单位根相关的乘积公式:
\[\prod_{k \text{ odd}} (z - \omega_n^k) = z^{\frac n 2} + 1\] \[\begin{aligned} \prod_{k=1}^{90} \lvert 1 - \omega_{180}^{2k-1} \rvert &= 2 \\ \prod_{k=1}^{45} \lvert 1 - \omega_{180}^{2k-1} \rvert &= \sqrt 2 \\ \prod_{k=1}^{45} \sin (2k-1)° &= \frac {\sqrt 2} {2^{45}} \\ \end{aligned}\]最终答案 $\boxed{2^{89}}$。
Sol 2
熟知 $\sin$ 的倍角公式
\[\boxed{ \prod_{k=0}^{n-1} 2 \sin \left( z + \frac k n \pi \right) = 2 \sin (nz) }\] \[\begin{aligned} & \prod_{k=1}^{45} \sin (2k-1)° \\ =& \frac 1 {2^{45}} \prod_{k=1}^{45} 2 \sin (2k-1)° \\ =& \frac 1 {2^{45}} \prod_{k=0}^{44} 2 \sin \left( \frac \pi {180} + \frac {k \pi} {90} \right) \\ =& \frac 1 {2^{45}} \sqrt{\prod_{k=0}^{89} 2 \sin \left( \frac \pi {180} + \frac {k \pi} {90} \right)} \\ =& \frac 1 {2^{45}} \sqrt{2 \sin(90 \frac \pi {180})} \\ =& \frac {\sqrt 2} {2^{45}} \\ \end{aligned}\]得到答案 $\boxed{2^{89}}$。
推导 Sol 2 使用的公式
我们从 Sol 1 的 $\sin$ 模长公式开始:
\[\lvert 2 \sin x \rvert = \lvert e^{2ix} - 1 \rvert\] \[\lvert 2 \sin (x + \frac k n \pi) \rvert = \lvert e^{2ix} e^{k \frac {2 \pi i} n} - 1 \rvert = \lvert e^{2ix} \omega_n^k - 1 \rvert = \lvert e^{2ix} - \omega_n^{-k} \rvert\] \[\prod_{k=0}^{n-1} \lvert 2 \sin (x + \frac k n \pi) \rvert = \lvert e^{2 inx} - 1 \rvert = \lvert 2 \sin(nx) \rvert\] \[\left\lvert \prod_{k=0}^{n-1} 2 \sin (x + \frac k n \pi) \right\rvert = \lvert 2 \sin(nx) \rvert\]接下来想办法去掉绝对值。注意到等式两边零点相同,所以我们只要随便找一个区间说明符号相同即可,$(0, \frac \pi n)$ 是一个不错的选择,两边所有 $\sin$ 函数全都是正的。
感性理解的话,可以考虑 $\sin x = x \prod_{k=1}^\infty (1 - (\frac x {k \pi})^2)$,非常像多项式,那 $\sin$ 的表现(除了一个常数以外)完全由零点决定也是比较合理的了。
Example 5.6 MPFG 2019 #20 (Normal)
\[\prod_{k=2}^\infty \left( 1 - 4 \sin^2 \frac \pi {3 \times 2^k} \right)\]
发动注意力:
\[\begin{aligned} & 1 - 4 \sin^2 x \\ =& 4 \cos^3 x - 3 \\ =& \frac {\cos 3x} {\cos x} \end{aligned}\]恭喜你最难的一步做完了,后续全是机械化推导。
官方做法
看到 $\cos(\frac \theta {2^k})$ 的结构,考虑一个二倍角的裂项:
\[\cos x = \frac 1 2 \frac {\sin 2x} {\sin x}\] \[\prod_{k=2}^n \cos(\frac \theta {2^k}) = \frac 1 {2^{n-1}} \frac {\sin \frac \theta 2} {\sin \frac \theta {2^n}}\]代入 $\theta = \pi$ 和 $\theta = \frac \pi 3$ 得到:
\[\prod_{k=2}^n \frac {\cos \frac \pi {2^k}} {\cos \frac \pi {3 \times 2^k}} = 2 \frac {\sin \frac \pi {3 \times 2^n}} {\sin \frac \pi {2^n}}\]令 $\alpha$ 为 $\frac \pi {3 \times 2^n}$:
\[\frac {\sin \alpha} {\sin 3 \alpha} = 3 - 4 \sin^2 \alpha\] \[\lim_{\alpha \to 0} \frac 2 {3 - 4 \sin^2 \alpha} = \boxed{\frac 2 3}\]我的做法
模仿 Example 5.2 的模长做法。
\[0 \le x \le \frac \pi 2 \implies \cos x = \frac 1 2 \lvert e^{2ix} - 1 \rvert\] \[\begin{aligned} & \prod_{k=2}^n \frac {\cos \frac \pi {2^k}} {\cos \frac \pi {3 \times 2^k}} \\ =& \prod_{k=2}^n \frac {\lvert e^{\frac {2 \pi i} {2^k}} - 1 \rvert} {\lvert e^{\frac {2 \pi i} {3 \times 2^k}} - 1 \rvert} \\ =& \left\lvert \prod_{k=2}^n \frac {\omega_{2^k} + 1} {\omega_{3 \times 2^k} + 1} \right\rvert \\ \end{aligned}\]这种 $2^k$ 一堆的东西,很容易联想到平方差的裂项:
\[\omega_{2^k} + 1 = \frac {\omega_{2^{k-1}} - 1} {\omega_{2^k} - 1}\] \[\prod_{k=2}^n (\omega_{2^k} + 1) = \frac {\omega_2 - 1} {\omega_{2^n} - 1}\]对分母可以进行一样的操作。
\[\begin{aligned} & \prod_{k=2}^n \frac {\omega_{2^k} + 1} {\omega_{3 \times 2^k} + 1} \\ =& \frac {\omega_2 - 1} {\omega_{2^n} - 1} \div \frac {\omega_6 - 1} {\omega_{3 \times 2^n} - 1} \\ =& \frac {\omega_2 - 1} {\omega_6 - 1} \times \frac {\omega_{3 \times 2^n} - 1} {\omega_{2^n} - 1} \\ =& 2 \omega_6 \times \frac 1 {\omega_{3 \times 2^n}^2 + \omega_{3 \times 2^n} + 1} \end{aligned}\] \[\begin{aligned} & \lim_{n \to \infty} \left\lvert \prod_{k=2}^n \frac {\omega_{2^k} + 1} {\omega_{3 \times 2^k} + 1} \right\rvert \\ =& \boxed{\frac 2 3} \end{aligned}\]Example 5.4 AIME I 2024 #12 (Easy)
定义函数
\[F(x) = 4 \lvert \lvert \lvert x \rvert - \frac 1 2 \rvert - \frac 1 4 \rvert\]求出以下两个图像的交点个数:
\[\begin{cases} y = F(\sin(2 \pi x)) \\ x = F(\cos(3 \pi y)) \\ \end{cases}\]
考虑刻画增减区间的条件,直接手玩规律。
首先先把 $F$ 画出来:
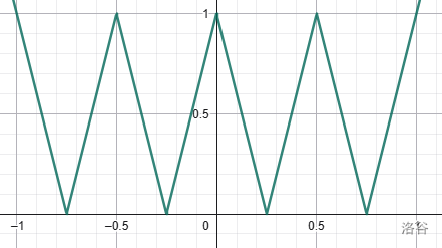
由于 $F$ 接受的是三角函数值,我们只在意 $[-1, 1]$ 的区间。不难发现这段上 $F$ 的值域是 $[0,1]$,也就是说我们只要关心 $x \in [0,1]$ 且 $y \in [0,1]$ 的范围。
对于 $x$ 的一个长度为 $\frac 1 4$ 的增 / 减区间,$F(x)$ 会经过一个完整的 W 形;对于 $y$ 的一个长度为 $\frac 1 6$ 的增 / 减区间,$F(x)$ 会经过一个完整的 W 形。
对于这样的一个 $\frac 1 4 \times \frac 1 6$ 的矩形,两个 W 会产生 $16$ 个交点,而这样的矩形有 $24$ 个。
特别地,$x=1, y=1$ 也是一个交点。总共有 $24 \times 16 + 1 = \boxed{385}$ 个交点。
Example 5.5 MPFG 2023 #20 (Normal)
令 $f(x) = 2 \pi \sin x$。令 $f^{(n)}$ 为 $f$ 的 $n$ 次复合。 求出满足以下条件的区间 $[l,r]$ 的个数:
- $0 \le l < r \le 2 \pi$
- $f^{(6)}(l) = -2 \pi, f^{(6)}(r) = 2 \pi$
- $f^{(6)}$ 在区间内单调递增
考虑刻画增减区间的条件,直接手玩规律。
手玩发现:
- 每个增减区间的值域都会完整覆盖 $[0, 2\pi]$ 或 $[-2\pi, 0]$,不会断开。
- 一个增区间在一次 $f$ 后被映射为“增减减增”,减区间被映射为“减增增减”。
- 我们要求的 $[-2\pi, 2\pi]$ 增区间即为“增增”。
现在题目和三角函数没有关系了,可以这样转化:
- 初始时有一个字符串
↑。 - 每次迭代会把
↑映射到↑↓↓↑,把↓映射到↓↑↑↓。 - 求 $6$ 次迭代后字符串中有几个
↑↑。
接着玩规律,发现每个 ↑↑ 都只能由 ↓ 迭代出来,而且迭代出来之后不会消失。也就是说,第 $n$ 次中 ↑↑ 的个数等于前 $n-1$ 次中 ↓ 的总数。
而除了初始时以外每次 ↑ ↓ 各占一半,不难发现第 $n$ 次时 ↓ 的个数应该是 $2^{2n-1}$。
因此答案为
\[\sum_{n=1}^5 2^{2n-1} = \boxed{682}\]