Lesson 5 信息论与决策树
Published:
信息量
设事件「随机变量 $X$ 取到 $x$」的信息量记为 $I(x)$。一个事件的信息量应该只和它发生的概率 $p$ 有关,所以 $I(x)$ 应该也是一个关于 $p$ 的函数 $h(p)$。
根据我们对“信息量”的朴素直觉,多个独立事件同时发生的总信息量等于每个事件信息量的和:
\[h(p_1 p_2) = h(p_1) + h(p_2)\]这是一个 Cauchy 方程,其解为
\[\boxed{ h(p) = C \ln p }\]虽然信息量是一个无量纲数,但人们喜欢赋予一个单位来解释它:对于一个发生概率为 $\frac 1 2$ 的事件(比如抛硬币得到正面),可以用一个 $1$ 位的二进制数来标记它。我们认为这种事件所含的信息量为 $1$ bit。
\[\begin{aligned} C \ln \frac 1 2 &= 1 \text{ bit} \\ C &= - \frac 1 {\ln 2} \text{ bit} \\ \end{aligned}\]因此,在以 bit 作单位时:
\[\boxed{ h(p) = - \log_2 p = \log_2 \frac 1 p }\] \[I(X) = - \log_2 P(X)\]例子:
- 抛硬币的结果有 $1$ bit 信息。
- 抛四面骰子的结果有 $2$ bit 信息。
- 抛八面骰子的结果有 $3$ bit 信息。
- 抛六面骰子的结果有 $\log_2 6$ bit 信息。
当然,以 $2$ 为底在数学上是不自然的。因此也有以 $e$ 为底的信息量 $I(X) = - \ln P(X)$,此时单位由 bit 改为 nat。
条件信息量
概率有条件版本,信息量也有条件版本:
\[I(Y \mid X) = - \log_2 P(Y \mid X)\]条件信息量也有 Bayes:
\[\begin{aligned} I(y \mid x) &= - \log_2 P(y \mid x) \\ &= - \log_2 \frac {P(x \cap y)} {P(x)} \\ &= (- \log_2 P(x \cap y)) - (- \log_2 P(x)) \\ &= I(x,y) - I(x) \\ \end{aligned}\]即:
\[I(Y \mid X) = I(X, Y) - I(X)\]信息熵
一个随机变量 $X$ 能带来的信息量 $I(X)$ 的期望称为信息熵 $H(X)$:
\[\boxed{\begin{aligned} H(X) &:= \mathbb E[I(X)] \\ &= - \sum_x P(x) \log_2 P(x) \end{aligned}}\]特别地,一个概率为 $0$ 的事件对信息熵的贡献为:
\[\begin{aligned} & \lim_{p \to 0^+} - p \ln p \\ =& \lim_{p \to 0^+} \frac {\ln \frac 1 p} {\frac 1 p} \\ =& \lim_{t \to \infty} \frac {\ln t} t \\ =& 0 \\ \end{aligned}\]信息熵可以衡量一个随机变量的不确定性,或者说混乱程度:
- 信息熵的最小值很容易想到:一个永远只能抛出正面的硬币(即确定事件),它的信息熵是 $0$。
- 最大值呢?
对于一个可灌铅的 $n$ 面骰子,应该怎么分配概率使得它的结果 $X$ 的信息熵 $H(X)$ 最大?
记 $h(p) = - p \log_2 p$。
我们希望找一个不等式限制住 $H(X) = \sum_{i=1}^n h(p_i)$,与此同时保持 $p_i \ge 0$ 和 $\sum_{i=1}^n p_i = 1$。
容易想到 Jensen 不等式:
\[\frac 1 n \sum_{i=1}^n h(p_i) \le h\left( \frac 1 n \sum_{i=1}^n p_i \right)\](计算一下会发现在 $p > 0$ 时 $h’‘(p) < 0$,即 $h$ 在 $(0, \infty)$ 上严格凹,确实满足 Jensen 不等式的使用条件)
\[\begin{aligned} H(X) = \sum_{i=1}^n h(p_i) & \le n h(\frac 1 n) \\ &= \log_2 n \end{aligned}\]在 $p_1 = \cdots = p_n = \frac 1 n$ 时取等。
因此,信息熵的最大值在均匀分布取到,为 $H(X) = \log_2 n$。
感性理解:骰子没有偏好才最难预测,当然不确定性最大。
联合信息熵
多个变量可以定义联合信息熵:
\[\begin{aligned} H(X,Y) &:= \mathbb E[I(X,Y)] \\ &= - \sum_{x,y} P(x,y) \log_2 P(x,y) \\ \end{aligned}\]条件信息熵
对 $I(Y \mid X)$ 用全期望公式:
\[\mathbb E[I(Y \mid X)] = \sum_x P(x) \mathbb E[I(Y \mid X = x)]\]我们就得到了信息熵的 Bayes 公式:
\[\boxed{ H(Y \mid X) = \sum_x P(x) H(Y \mid X = x) }\]我们还知道
\[\begin{aligned} I(Y \mid X) &= I(X, Y) - I(X) \\ I(X,Y) &= I(Y \mid X) + I(X) \\ \end{aligned}\]两边取期望:
\[\boxed{ H(X,Y) = H(Y \mid X) + H(X) \\ }\]信息增益
$X$ 对 $Y$ 造成的信息增益,就是看知道了 $X$ 之后 $Y$ 的不确定性下降了多少:
\[\boxed{ IG(Y, X) := H(Y) - H(Y \mid X) }\]有一个论坛。我们要考察用户的性别和活跃度哪个对流失率影响更大。
我们有 $15$ 个样本,$5$ 个正样本(确实流失了),$10$ 个负样本。
- 按性别分类:
- 男:$3$ 正 $5$ 负
- 女:$2$ 正 $5$ 负
- 按活跃度分类:
- 高:$0$ 正 $6$ 负
- 中:$1$ 正 $4$ 负
- 低:$4$ 正 $0$ 负
由于我们无法得知具体的概率,只能以相对频率作为概率的 MLE 用作估算。
具体来说,$V$ 是特征,$v$ 是 $V$ 的取值,$D$ 是数据集,$D^v$ 中 $V = v$ 的子集,则信息熵的估计值为:
\[\hat H(Y | V) = \sum_{v \in \operatorname{value}(V)} \frac {\lvert D^v \rvert} {\lvert D \rvert} \hat H(Y \mid D^v)\]注意这是一个有偏估计:
\[\mathbb E[\hat H] < H\]下文分析中为了方便,省略所有的 hat。
令随机变量 $Y \in {1, 0}$ 表示正 / 负样本。
计算 $Y$ 的信息熵:
\[\begin{aligned} H(Y) &= - \sum_y P(y) \log_2 P(y) \\ &= - (\frac 5 {15} \log_2 \frac 5 {15} + \frac {10} {15} \log_2 \frac {10} {15}) \\ & \approx 0.918 \text{ bit} \end{aligned}\]计算在已知性别时的 $Y$ 的条件信息熵:
\[\begin{aligned} H(Y \mid \text{male}) &= - \sum_y P(y \mid \text{male}) \log_2 \sum_y P(y \mid \text{male}) \\ &= - (\frac 3 8 \log_2 \frac 3 8 + \frac 5 8 \log_2 \frac 5 8) \\ & \approx 0.954 \text{ bit} \end{aligned}\] \[H(Y \mid \text{female}) = \cdots \approx 0.863 \text{ bit}\] \[\begin{aligned} H(Y \mid \text{gender}) &= \sum_x P(x) H(Y \mid X = x) \\ &= \frac 8 {15} H(Y \mid \text{male}) + \frac 7 {15} H(Y \mid \text{female}) \\ & \approx 0.912 \text{ bit} \end{aligned}\]计算性别这一特征带来的信息增益:
\[\begin{aligned} IG(Y, \text{gender}) &= H(Y) - H(Y \mid \text{gender}) \\ & \approx 0.918 \text{ bit} - 0.912 \text{ bit} \\ & \approx 0.006 \text{ bit} \end{aligned}\]通过同样的计算:
\[H(Y \mid \text{activity}) \approx 0.241 \text{ bit}\] \[\begin{aligned} IG(Y, \text{activity}) &= H(Y) - H(Y \mid \text{activity}) \\ & \approx 0.918 \text{ bit} - 0.241 \text{ bit} \\ & \approx 0.677 \text{ bit} \end{aligned}\]结论:活跃度带来的信息增益远大于性别。因此活跃度带来的影响更大。
决策树
这是一个决策树 (Decision tree) 的例子:
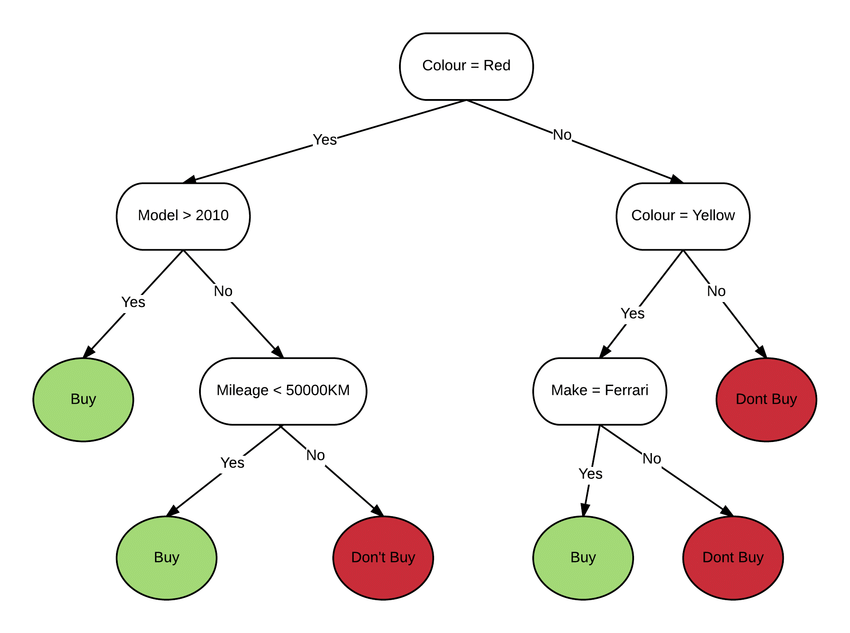
通过不断地 if else,最终得到输出。
基于信息论的决策树
ID3 决策树
用 $X_1, \cdots, X_n$ 这 $n$ 个特征,制造一棵决策树来预测 $Y$。怎样能够比较好地限制这棵树的大小?
e.g. 用性别和活跃度预测用户是否流失。
我们每次贪心地挑选信息增益最大的特征,然后递归建树。这被称为 ID3 算法(ID3 是 Iterative Dichotomiser 3 的缩写)。
C4.5 决策树
ID3 数学上很好,但是实际用的时候会发现其实很废物。
回到前面论坛的例子,假设现在多了一项特征为「用户 ID」。我们的 ID3 会发现「用户 ID」可以将所有人完美分类,然后再也不看「性别」和「活跃度」。此时这个模型泛化能力被大大削弱。
这告诉我们 ID3 算法一味看重信息增益是不行的,我们还应该关注一个特征会把数据分的多“稀碎”。不妨把信息增益和“稀碎度”的比值作为最大化的目标。“稀碎度”用符号 $IV$ 表示。
如何定义稀碎度?对于一个特征 $X$,不妨定义稀碎度为 $X$ 的取值分布的信息熵 $H(X)$:
\[IV(X) = H(X) = - \sum_{x} P(x) \log_2 P(x)\]稀碎度的正式名称叫 IV 特征熵。信息增益与 IV 特征熵的比值叫信息增益率 (gain ratio)。
\[\operatorname{GainRatio}(X) = \frac {IG(Y, X)} {IV(X)}\]通过贪心地最大化 gain ratio 建决策树的算法,被称为 C4.5 决策树。
CART 分类决策树
$H$ 计算太慢了,要算一堆 $\log$。
$H$ 衡量了一个随机变量出来的值有多杂乱,那还有没有其它的指标也可以衡量这一点?
定义随机变量 $X$ 的 Gini 值为独立取两次值后不一致的概率:
\[\boxed{ \text{Gini}(X) := 1 - \sum_x P(x)^2 }\]我们还可以定义它的条件版本,称为 Gini 指数 (Gini index):
\[\text{Gini}(Y \mid X = x) = 1 - \sum_y P(y \mid X = x)^2\]根据全概率公式可知:
\[\text{Gini}(Y \mid X) = \sum_x P(x) \text{Gini}(Y \mid X = x)\]通过贪心地最小化 Gini 指数建决策树的算法,被称为 CART 分类决策树 (classification and regression tree)。
但是注意 CART 和前面的 ID3 和 C4.5 不一致的地方在于,它坚持使用二叉树。也就是说,当它遇到多叉的特征时,它会选择其中几叉绑在一起,其它叉绑在一起,这样保持二叉。
当然,遇到 $k$ 叉时,它需要做 $\Theta(2^k)$ 次检查,这经常不可接受。但 ChatGPT 称,把每一叉按照叉内的正类概率排序后,由于 Gini 值的凸性,可结合 Jensen 不等式通过邻项交换证明最优解一定是切割成「前缀+后缀」的结构,此时只需要检查 $\Theta(k)$ 次。
让决策树支持连续值
有一个特征的取值 $X \in \mathbb R$。假设在我的样本中 $X$ 的取值为 $x_1 \le x_2 \cdots \le x_n$,决策树应该怎么处理?
对于每个 $i = 1, \cdots, n-1$,尝试分成 $\le x_i$ 和 $\ge x_{i+1}$ 两类。为了方便,习惯上直接取 $\frac {x_i + x_{i+1}} 2$ 作为分界点即可。
让决策树支持缺失数据
上课没讲。
ChatGPT 介绍了三种方式:
- 按概率赋权,把每条路都走。
- 找一个和它最一致的特征替代它。
- 让决策树学习缺失的样本应该默认走左还是右。
CART 回归决策树
我们尝试用 CART 解决最小二乘的问题。我们只保留二叉树的特性,忘掉 Gini 值。
首先用上文的办法解决输入为连续值的问题。然后为了获得连续的输出,我们让叶子的输出为叶子上所有样本的均值。每次划分的时候,让切分点的损失为左右两个叶子的损失之和即可,叶子的损失用最小二乘计算。每层贪心地选择损失最小的切分点。
这种方式称为 CART 回归决策树。
决策树剪枝
- 预剪枝:在建树的时候,只划分能让 loss 减小的。
- 后剪枝:建树完之后,对每个非叶子节点考察,剪掉剪了使 loss 减小的节点。
| 预剪枝 | 后剪枝 | |
|---|---|---|
| 优点 | 过拟合风险小,训练时间和测试时间开销小 | 欠拟合风险小,泛化性能高 |
| 缺点 | 欠拟合风险 | 训练时间开销大 |