Tongrui 5.3 方程
Published:
总结
- 非齐次的式子可以考虑先齐次化。
- 遇到根号加根号，先看是不是 $\sqrt{x-a} + \sqrt{y-a}$ 的结构，如果是就无脑构造三角形。
Example 5.16 HMMT 2025 Feb AN #7 (Easy)
\[\begin{cases} 2 (a^2 + 1) = 3 (b^2 + 1) = 4 (c^2 + 1) \\ ab + ac + bc = 1 \\ a, b, c > 0 \\ \end{cases}\]求 $a + b + c$。
齐次化。
\[\begin{aligned} & a^2 + 1 \\ =& a^2 + (ab + ac + bc) \\ =& (a + b) (a + c) \\ \end{aligned}\]用一样的手法处理：
\[2 (a+b) (a+c) = 3 (a+b) (b+c) = 4 (a+c) (b+c)\] \[\frac 2 {b+c} = \frac 3 {a+c} = \frac 4 {a+b}\]可以解出 $a
c = 5:3:1$。最终答案 $\boxed{\frac 9 {23} \sqrt{23}}$。
Example 5.14 AIME II 2006 #15 (Easy)
已知实数 $x,y,z$ 满足
\[\begin{align*} x &= \sqrt{y^2-\frac{1}{16}}+\sqrt{z^2-\frac{1}{16}}, \\ y &= \sqrt{z^2-\frac{1}{25}}+\sqrt{x^2-\frac{1}{25}}, \\ z &= \sqrt{x^2 - \frac 1{36}}+\sqrt{y^2-\frac 1{36}}, \end{align*}\]求 $x + y + z$。
Example 5.18 AIME I 2022 #15 (Normal)
正实数 $x,y,z$ 满足
\[\begin{align*} \sqrt{2x-xy} + \sqrt{2y-xy} &= 1 \\ \sqrt{2y-yz} + \sqrt{2z-yz} &= \sqrt2 \\ \sqrt{2z-zx} + \sqrt{2x-zx} &= \sqrt3. \end{align*}\]求 $((1-x)(1-y)(1-z))^2$。
Sol 1
对每个方程单独构造一个三角形：
TODO: 图画错了
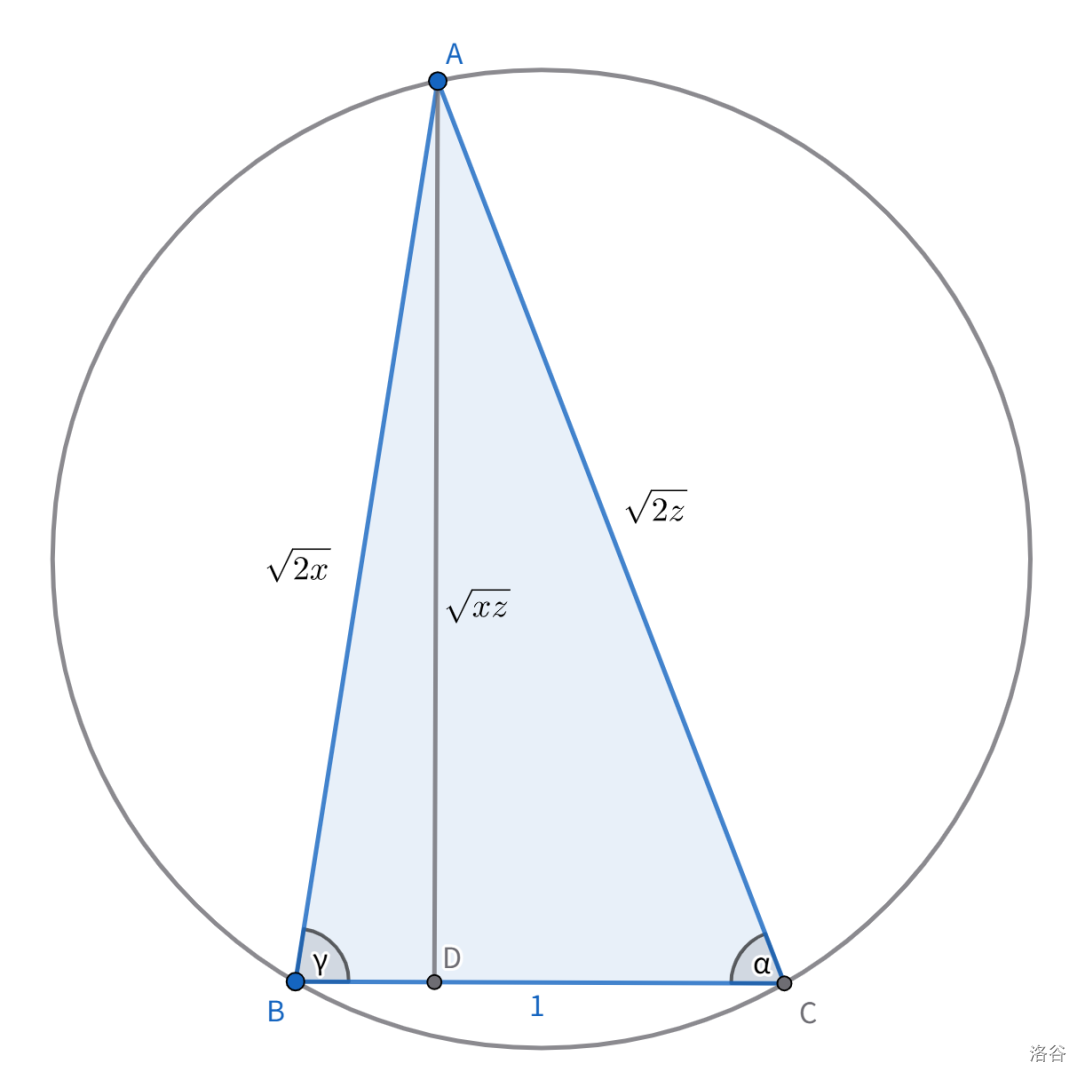
由于外接圆大小相同，$\sqrt{2x}, \sqrt{2y}, \sqrt{2z}$ 各自在不同三角形中所对的角是相同的，记为 $\alpha, \beta, \gamma$。
\[\begin{cases} x = 2 \sin^2 \alpha \\ y = 2 \sin^2 \beta \\ z = 2 \sin^2 \gamma \\ \end{cases}\] \[\begin{cases} \alpha + \gamma = 180° - \arcsin \frac 1 2 \\ \beta + \gamma = 180° - \arcsin \frac {\sqrt 2} 2 \\ \alpha + \beta = 180° - \arcsin \frac {\sqrt 3} 2 \\ \end{cases} \implies \begin{cases} \alpha = \frac {135} 2° \\ \beta = \frac {105} 2° \\ \gamma = \frac {165} 2° \\ \end{cases}\] \[\begin{aligned} & ((1-x)(1-y)(1-z))^2 \\ =& ((1 - 2 \sin^2 \alpha) (1 - 2 \sin^2 \beta) (1 - 2 \sin^2 \gamma))^2 \\ =& (\sin(2 \alpha) \sin(2 \beta) \sin(2 \gamma))^2 \\ =& \boxed{\frac 1 {32}} \\ \end{aligned}\]Sol 2
\[\sqrt x \sqrt{2 - y} + \sqrt y \sqrt{2 - x} = \square\]这个结构让人联想到
\[\sin A \cos B + \sin B \cos A\]又注意到 $(\sqrt x)^2 + (\sqrt{2-x})^2 = 2$，考虑做一个 $\sqrt 2$ 倍的缩放：
\[\sqrt {\frac x 2} \sqrt{\frac {2 - y} 2} + \sqrt {\frac y 2} \sqrt{\frac {2 - x} 2} = \frac \square 2\]换元 $\sin A = \sqrt {\frac x 2}, \sin B = \sqrt {\frac y 2}$：
\[\sin A \cos B + \sin B \cos A = \frac \square 2\]后续做法一致。