Tongrui 1 几何 Part 1【施工中】
Published:
这一段部分题目比较水或者只需要特定的观察,因此只记有价值 / 有借鉴意义的部分。
公式 / 模型
为了防止文章太长太卡,把很多点做成了单独的文章:
Euler 定理与 Euler 不等式
练习题:Example 1.9 AIME II 2024 #10
三角形 $ABC$ 中,内心为 $I$,外心为 $O$,内切圆、外接圆半径为 $r,R$。
证明:两心之间的距离 $OI$ 只由 $R,r$ 决定,并求出具体表达式。
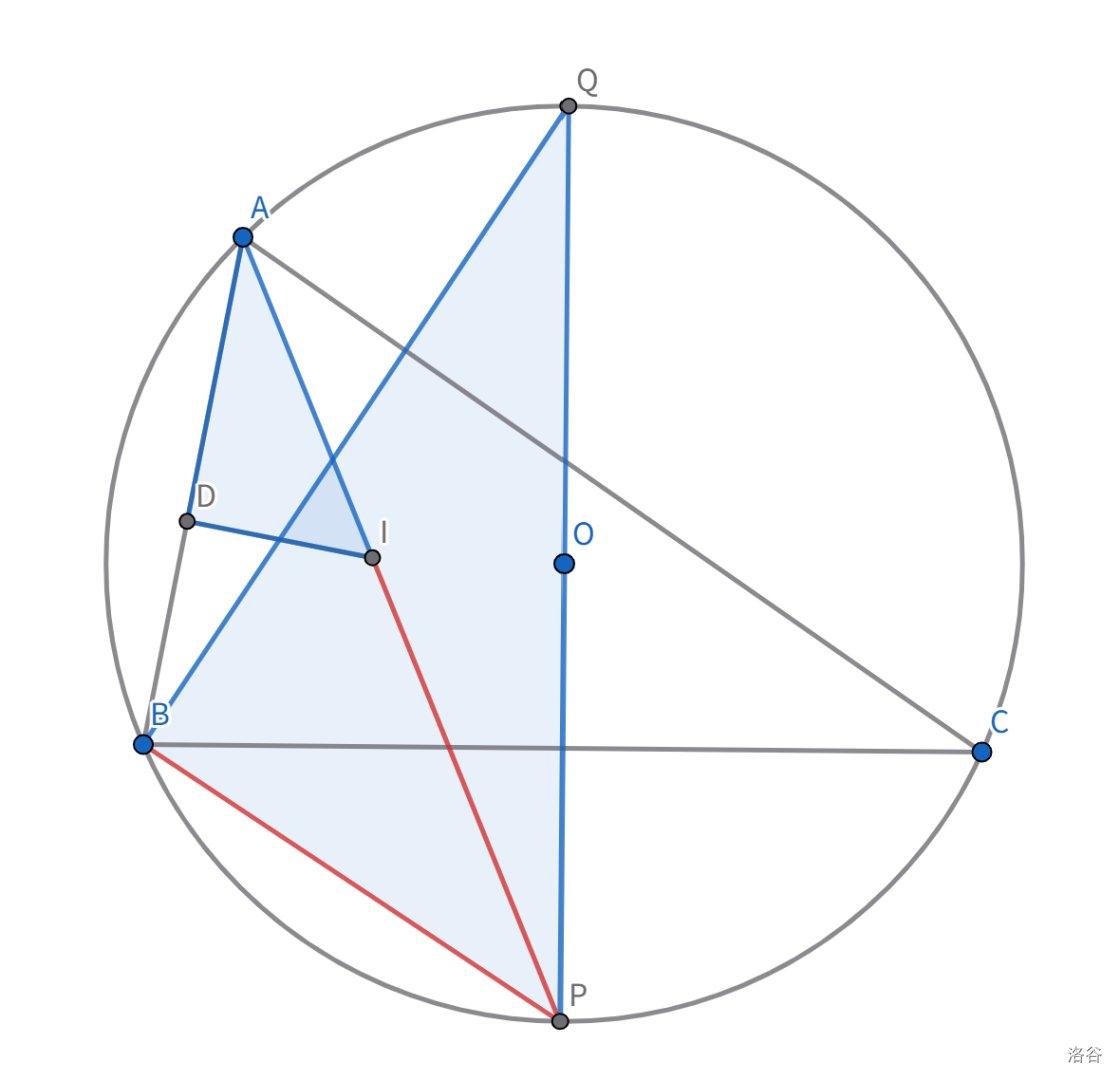
求 $OI$ 等价于求 $I$ 对圆 $O$ 的幂。为了使用圆幂,我们要在图中找一条合适的过 $I$ 的弦。对于内心 $I$ 来说,最合适的肯定就是它和一个顶点的的连线。
\[\Pi_O(I) = OI^2 - R^2 = - AI \times IP\]根据鸡爪定理,$IP = BP$。接下来我们只要把 $AI \times BP$ 表示成 $R,r$ 的形式即可。
构造图中这对蓝色相似三角形,得:
\[\begin{aligned} \frac r {BP} &= \frac {AI} {2R} \\ AI \times BP &= 2Rr \\ AI \times IP &= 2Rr \\ OI^2 - R^2 &= -2Rr \\ \end{aligned}\]最终得到
\[\Pi_O(I) = OI^2 - R^2 = - 2Rr\] \[\boxed{ OI^2 = R (R - 2r) }\]推论(Euler 不等式):
\[\boxed{ R \ge 2r }\]取等条件为 $OI = 0$,即三角形为等边三角形。
角元 Menelaus 与 Ceva 定理
TODO:
Example 1.5 AIME II 2002 #14 (Normal)
暴算勾股定理太困难,改用三角函数,将勾股定理完全打包在三角函数的内在性质中。
类似题目:Example 1.19
直角三角形 $APM$ 中,$A$ 是直角,周长为 $152$。在边 $AP$ 上取一点 $O$ 为圆心画一个半径为 $19$ 的圆,正好和 $AM$ 与 $PM$ 都相切。求 $OP$。
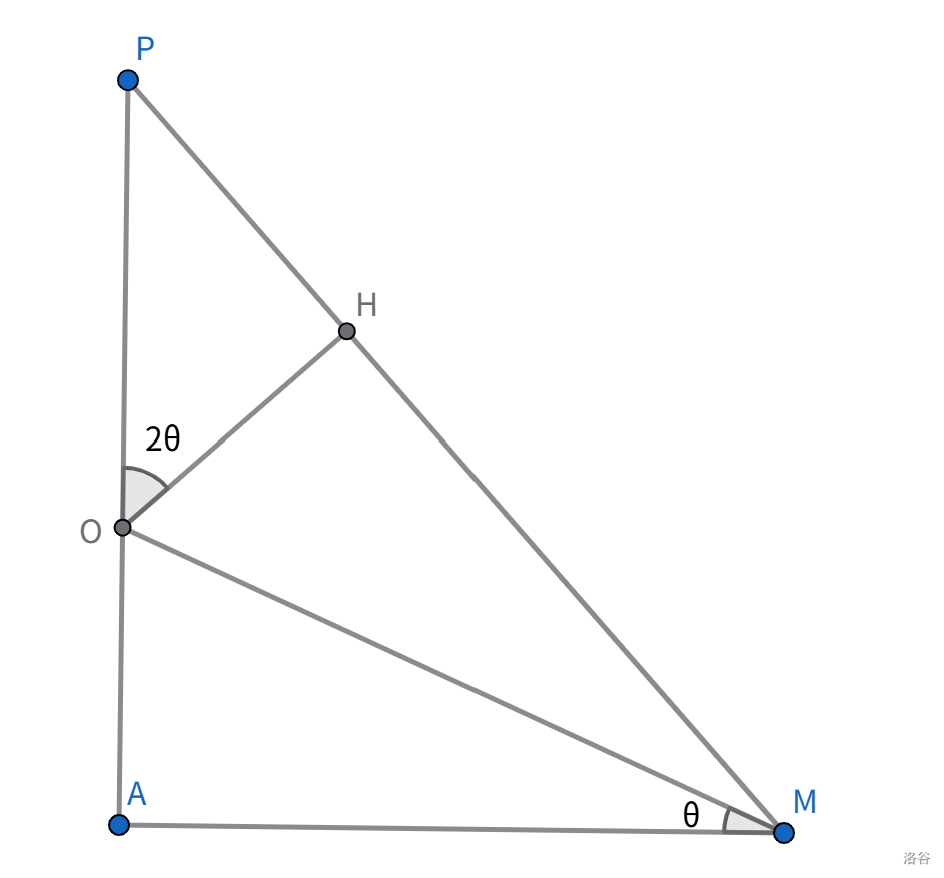
拿到题目的第一反应是用勾股定理列一堆方程开始硬解,显然非常麻烦!我们可以用三角函数来刻画这个问题。
\[19 (1 + 2 \cot \theta + \tan 2 \theta + \sec 2 \theta) = 152\] \[2 \cot \theta + \tan 2 \theta + \sec 2 \theta = 7\]同时出现 $\theta$ 和 $2 \theta$,万能公式是一个不错的选择。
设 $t = \tan \theta$,有 $\tan 2 \theta = \frac {2t} {1 - t^2}$,$\sec 2 \theta = \frac {1 + t^2} {1 - t^2}$。
\[\frac 2 t + \frac {2t} {1 - t^2} + \frac {1 + t^2} {1 - t^2} = 7\]解出 $t = \frac 1 2$,$\sec 2 \theta = \frac 5 3$。答案为 $19 \times \frac 5 3 = \boxed{\frac {95} 3}$。
Example 1.8 AIME II 2020 #13
TODO:
Example 1.11 AIME I 2023 #12 (Normal)
Solution 3 的解法
TODO:
结论:在等边三角形中,
- 三条红线之和为定值,为一条高的长度。
- 三条绿线之和等于三条蓝线之和为定值,为半周长。
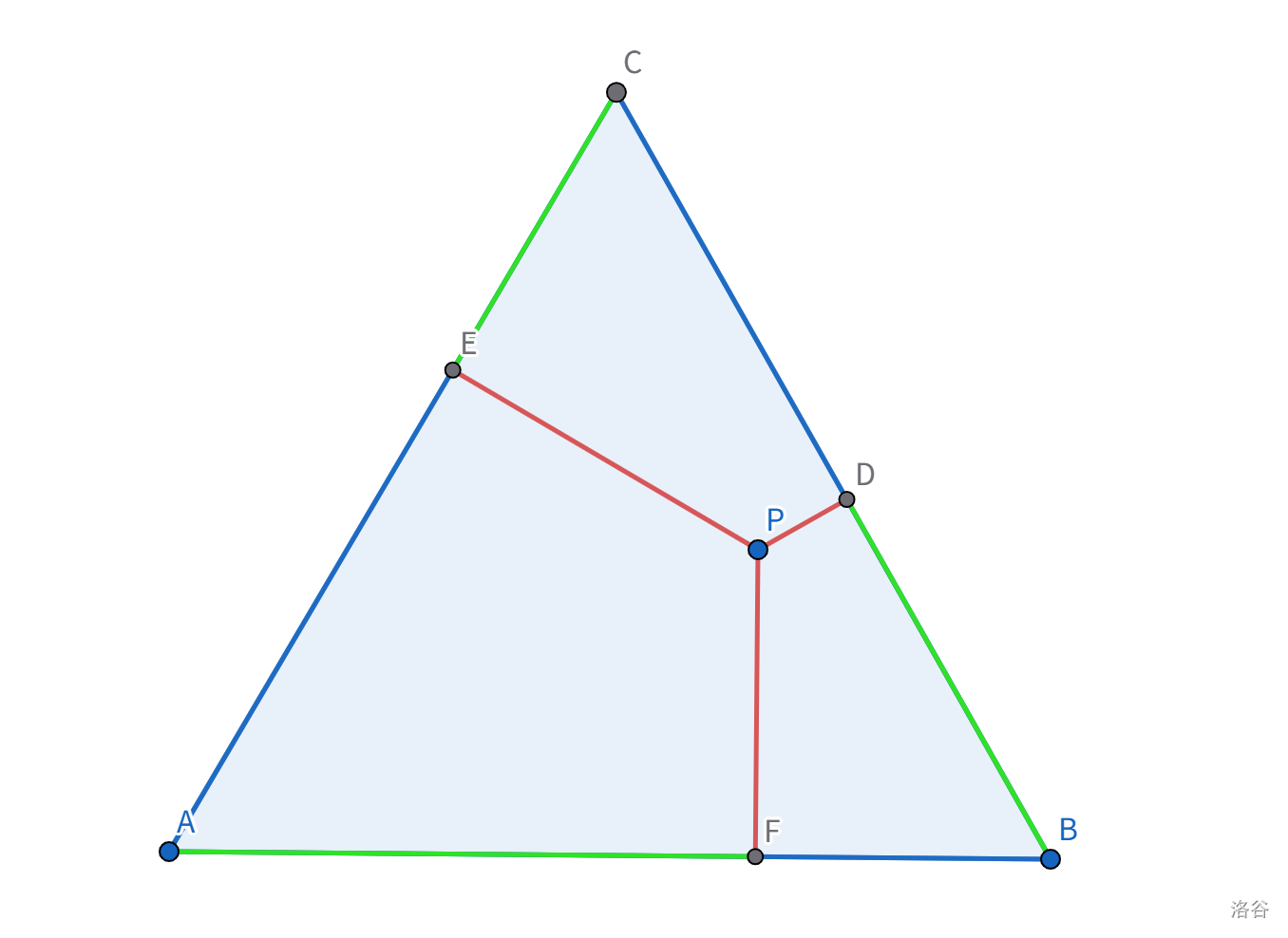
TODO:
Example 1.12 AIME II 2021 #14
TODO: Simson 线
Example 1.14 (Normal)
TODO:
Example 1.15 AIME I 2016 #15 (Hard)
神题!几何机械化思考的典范。
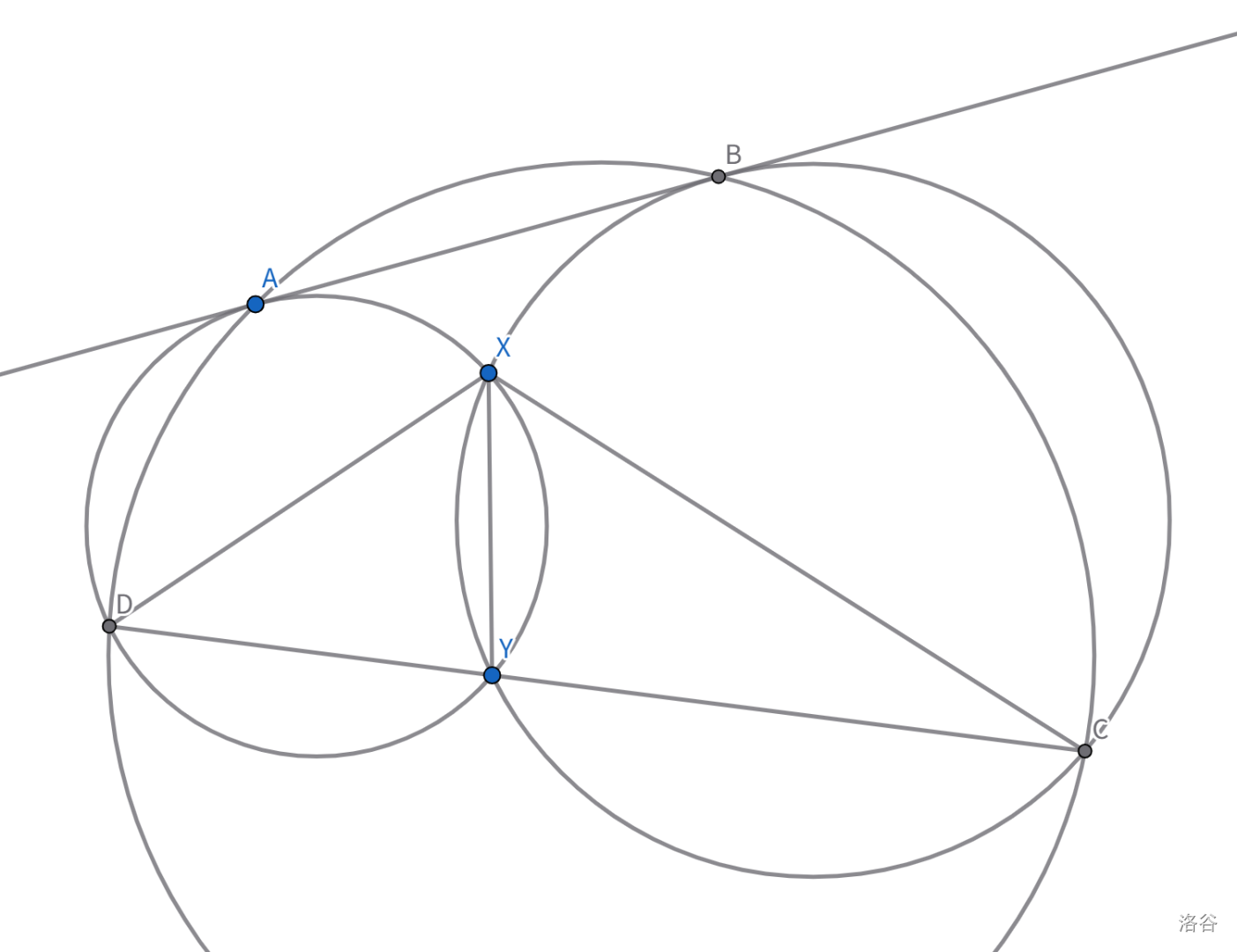
有两个圆 $\omega_1, \omega_2$ 交于 $X,Y$。作它们的一条公切线,切点为 $A,B$。
又有一个圆 $\omega_3$,它和 $\omega_1$ 交于 $D$,和 $\omega_2$ 交于 $C$。$D,Y,C$ 恰好三点共线。
已知 $XC = 67, XD = 37$ 以及 $XY = 47$。
求 $AB^2$。
相交圆公切线,辅助线肯定要作它们的公共弦(根轴),延长公共弦与公切线交于 $Z$,有经典结论 $AZ=BZ$。
三个圆的三个根轴交于根心,所以我们延长 $DA, CB, YX$,三线共点交于根心 $P$。
对三角形 $CDP$ 使用 Miquel 定理,得到 $AXBP$ 四点共圆。
对于圆 $AXBP$ 使用圆幂定理,$AZ^2 = ZX \times ZP$。同时我们前面在观察 1 的经典结论中已经知道了 $AZ^2 = ZX \times ZY$,可得 $ZP = ZY$。
由 $ZP=ZY$ 且 $ZA=ZB$ 可得 $AYBP$ 是平行四边形。四点共圆导出相似 $\triangle DXP \sim \triangle PXC$。算出 $PX = \sqrt{37 \times 67}$。
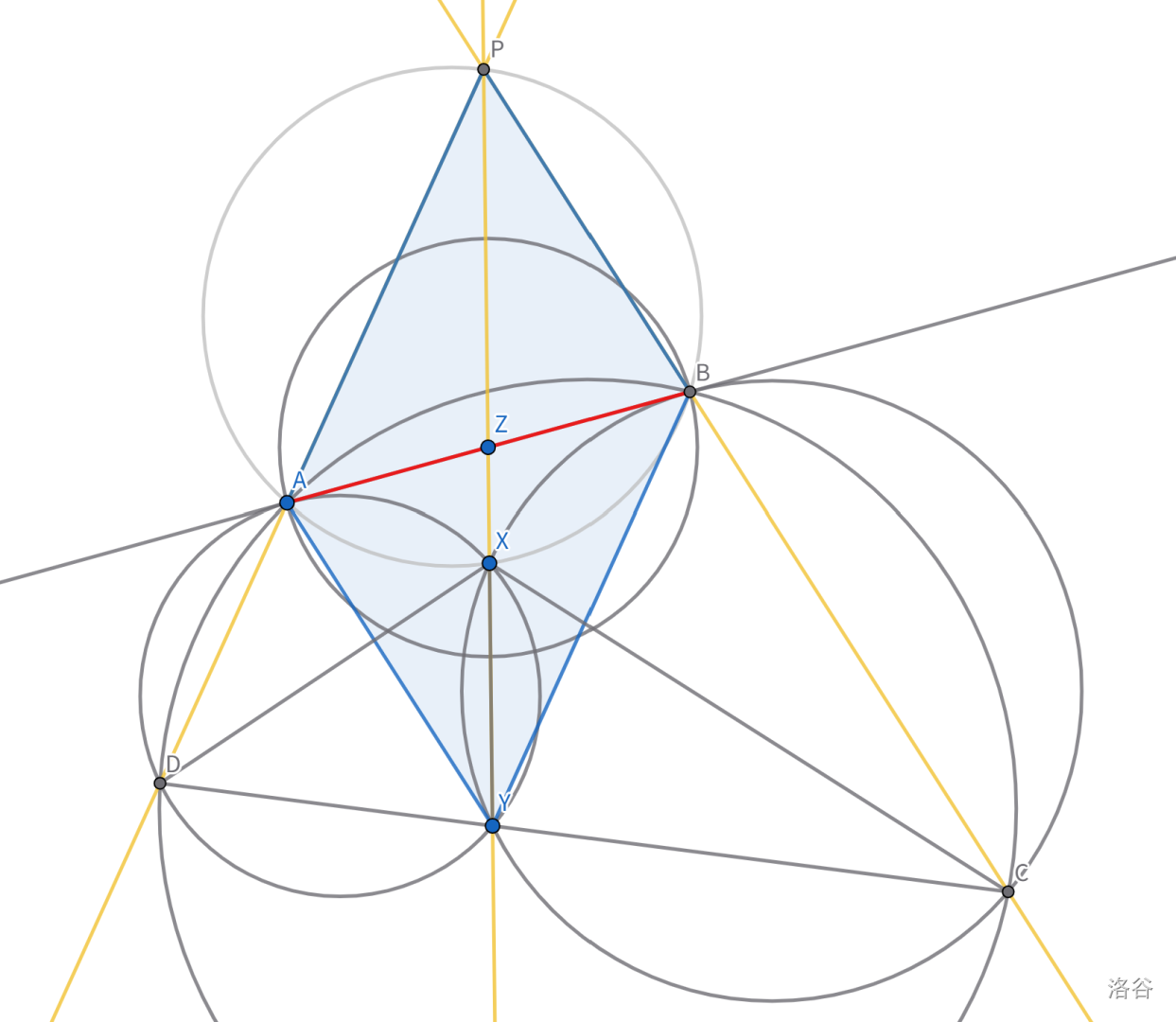
此时 $PY$ 上的所有边都能算了。最后可以得到 $AB^2 = 37 \times 67 - 47^2 = \boxed{270}$。
Example 1.18 AIME I 2009 #12 (Normal)
TODO:
Example 1.19 AIME I 2019 #11 (Hard)
类似题目:Example 1.5
这是我第一次遇到「勾股定理换三角函数」这个 Trick 的题目,大受震撼。
有一个三边均为整数的等腰三角形 $ABC$,$A$ 为顶角,内心为 $I$,三个旁心为 $I_A, I_B, I_C$。
已知存在一个圆的圆心为内心 $I$,与旁切圆 $I_A$ 内切,与旁切圆 $I_B, I_C$ 外切。
求三角形 $ABC$ 的最小周长。
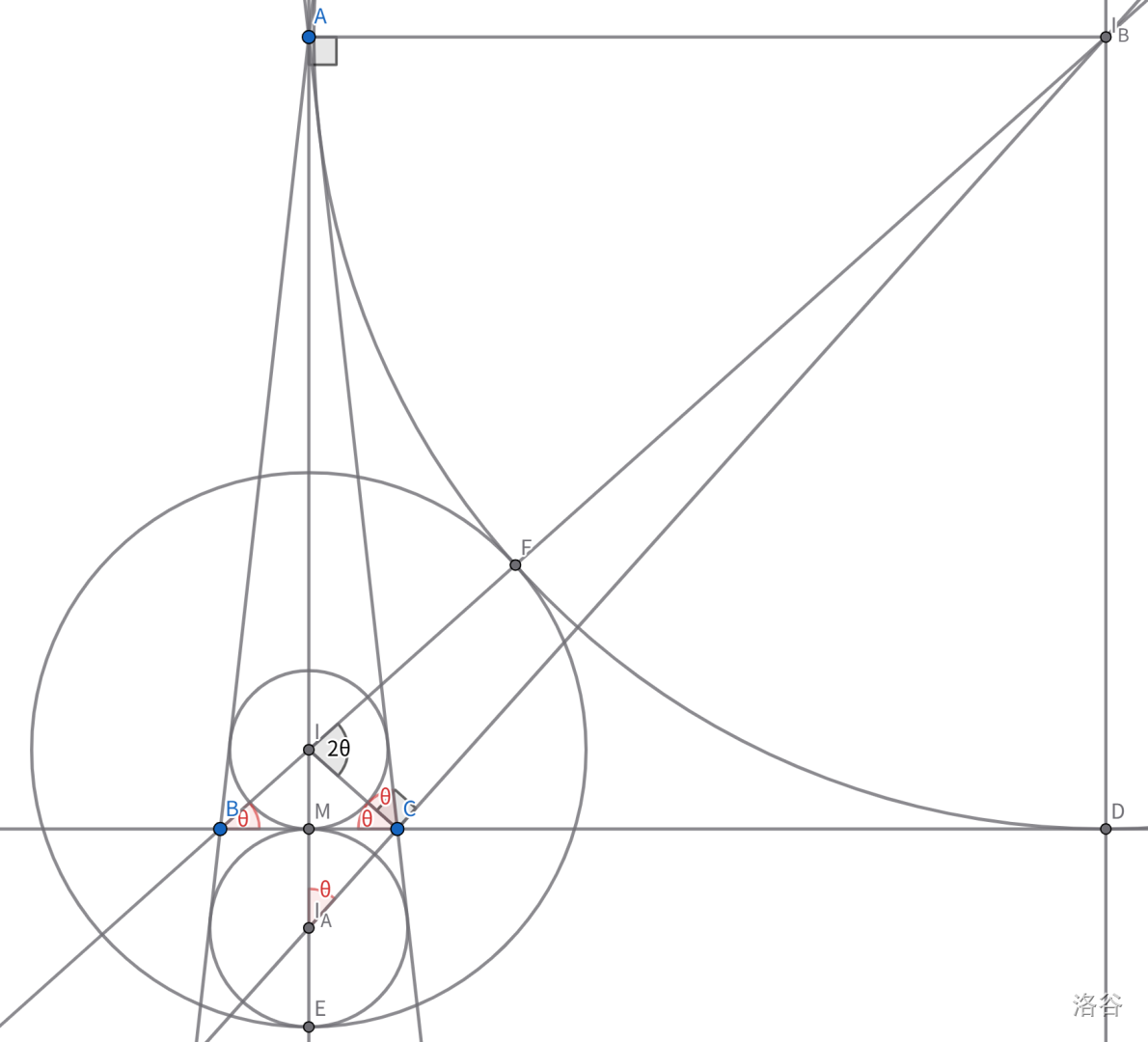
勾股定理太烦,用三角函数做。
根据题目条件:
\[r + 2 r_A = I I_B - r_B\]令 $a = MC$,$\theta = \angle MCI$。依次求出:
\[\begin{cases} r = a \tan \theta \\ r_A = a \cot \theta \\ r_B = AM = a \tan 2 \theta \\ I I_B = IC \sec 2 \theta = a \sec \theta \sec 2 \theta \\ \end{cases}\]代入并约掉 $a$:
\[\tan \theta + 2 \cot \theta = \sec \theta \sec 2 \theta - \tan 2 \theta\]解得
\[\sec 2 \theta = 9\] \[AC = a \sec2 \theta = 9a = \frac 9 2 BC\]因此最小的情况是 $BC = 2, AC = 9$,答案为 $\boxed{020}$。
这个三角方程具体怎么解?
TODO:
Example 1.20 (Hard)
Example 1.22 (Hard)
Example 1.23 (Hard)
Example 1.24
Example 1.25 AIME II 2012 #15
Example 1.32 AIME II 2002 #15 (Hard)
评价为高考题
Example 1.34 AIME I 2005 #14 (Normal)
向量??
Example 1.35 AIME I 2007 #12 (Normal)
叉乘
Example 1.36 AIME I 2010 #13 (Normal)
加强:只知道 $AN$ 是代数数,不知道 $AN$ 的具体值。
https://artofproblemsolving.com/wiki/index.php?title=2005_AIME_II_Problems/Problem_14
https://artofproblemsolving.com/wiki/index.php?title=2012_AIME_I_Problems/Problem_13