Tongrui 5.4 复数
Published:
复数
模长和共轭
\[\lvert z \rvert = \sqrt{z \bar z}\]要求模长的时候,考虑构造共轭。
模长的三角形不等式
\[\lvert \lvert z_1 \rvert - \lvert z_2 \rvert \rvert \le \lvert z_1 + z_2 \rvert \le \lvert z_1 \rvert + \lvert z_2 \rvert\]单位根
\[\prod_{k=0}^{n-1} (z - \omega_n^k) = z^n - 1\]对于偶数 $n$:
\[\prod_{k \text{ odd}} (z - \omega_n^k) = z^{\frac n 2} + 1\]单位根反演
\[[n \mid k] = \frac 1 n \sum_{i=0}^{n-1} \omega_n^{ik}\] \[\sum_{n \mid k} [x^k] f(x) = \frac 1 n \sum_{i=0}^{n-1} f(\omega_n^i)\]Example 5.25 AIME II 2024 #13 (Easy)
\[\prod_{k=0}^{12} (\omega_{13}^{2k} - 2 \omega_{13}^k + 2)\]\[\begin{aligned} & \prod_{k=0}^{12} (\omega_{13}^{2k} - 2 \omega_{13}^k + 2) \\ =& \prod_{k=0}^{12} ((1 + i) - \omega_{13}^k) ((1 - i) - \omega_{13}^k) \\ =& ((1+i)^{13} - 1) ((1-i)^{13} - 1) \\ =& \boxed{8321} \\ \end{aligned}\]
Example 5.21 AIME II 2008 #13 (Normal)
复平面上有一个边长为 $\frac 1 {\sqrt 3}$ 且中心在原点的正六边形,有一组对边与虚轴平行。
设该六边形以外的区域为 $R$,对 $R$ 中的所有复数作变换 $z \mapsto \frac 1 z$,求 $R$ 变换完后的面积。
由于有对称性,为了方便,我们把变换改为 $z \mapsto \frac 1 {\bar z}$,这样辐角不变。这样容易看出,这个变换此时只和 $\lvert z \rvert$ 有关,也就是说它是各向同性的。
Sol 1
我们可以把六边形改成 $12$ 个小三角形分别计算面积。
考虑最右边这条边,辐角为 $\theta$ 处的模长为 $\frac 1 2 \sec \theta$,反演后为 $r = 2 \cos \theta$。
\[\begin{aligned} & \frac 1 2 \int_0^{\frac \pi 6} r^2 d\theta \\ =& \frac 1 2 \int_0^{\frac \pi 6} (2 \cos \theta)^2 d\theta \\ =& 2 \int_0^{\frac \pi 6} \frac {\cos 2 \theta + 1} 2 d\theta \\ =& \frac \pi 6 + \frac {\sqrt 3} 4 \\ \end{aligned}\] \[\text{Area} = 12 \times \left( \frac \pi 6 + \frac {\sqrt 3} 4 \right) = \boxed{2 \pi + 3 \sqrt 3}\]Sol 2
这个变换是关于单位圆的反演变换。熟知结论反演变换保广义圆不变,直线在反演变换下会变成圆或保持直线。
我们可以直接画出变换后的样子:
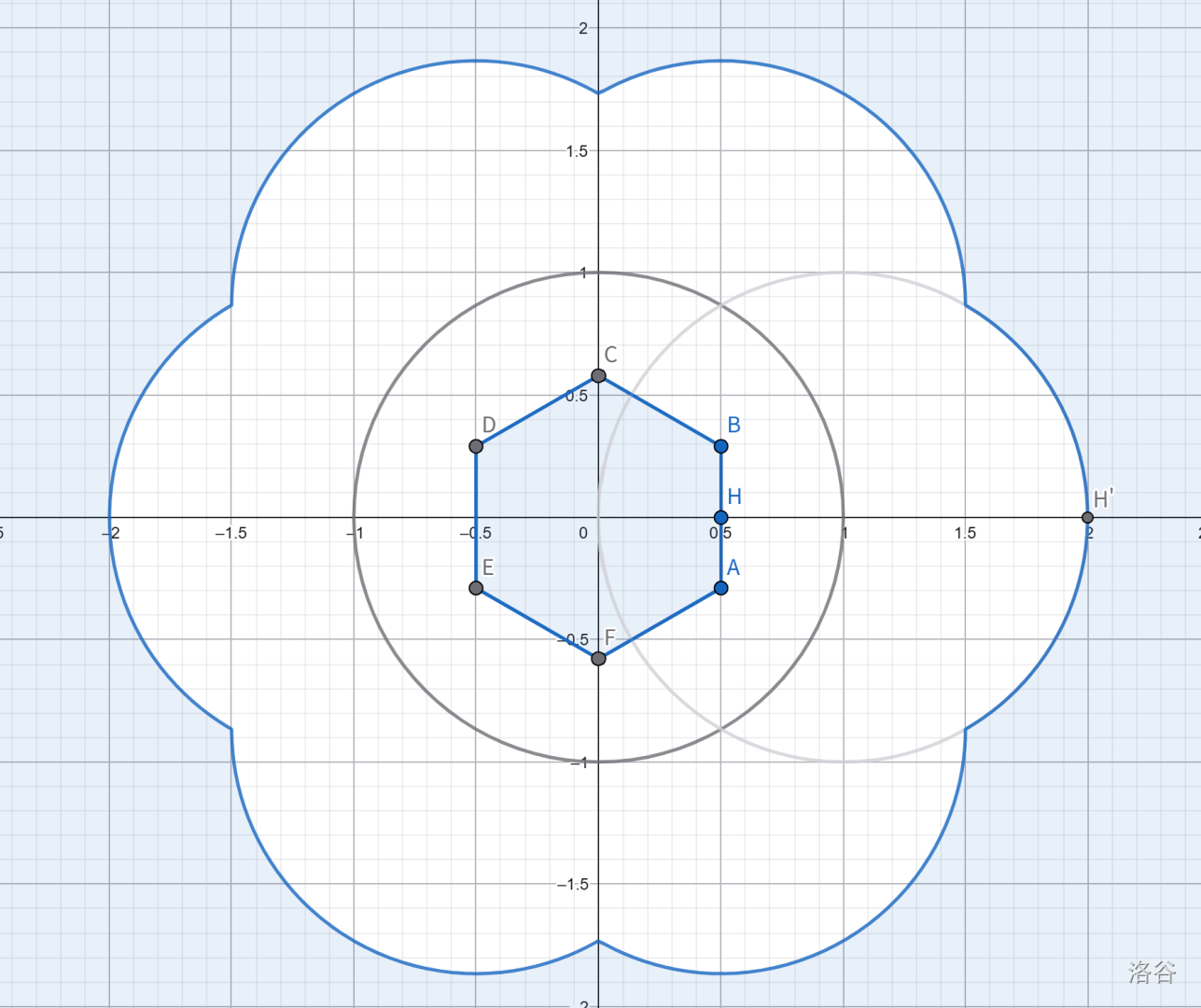
这个图的面积是十分容易计算的,可得 $\boxed{2 \pi + 3 \sqrt 3}$。
Example 5.19 CHKMO 2021 #4 (Normal)
这个题目好像有高等背景。A099390
\[\begin{aligned} & \prod_{k=1}^n (1 + 4 \cos^2 \frac {k \pi} {2n+1}) \\ =& \prod_{k=1}^n \left( 3 + 2 \cos (k \times \frac {2 \pi} {2n+1}) \right) \\ =& \prod_{k=1}^n (3 + \omega_{2n+1}^k + \omega_{2n+1}^{-k}) \\ =& \sqrt{ \frac 1 5 \prod_{k=0}^{2n} (3 + \omega_{2n+1}^k + \omega_{2n+1}^{-k})} \end{aligned}\]证明:对任意正整数 $n$,$\prod_{k=1}^n (1 + 4 \cos^2 \frac {k \pi} {2n+1})$ 是整数。A001519
令 $m = 2n+1$:
\[\begin{aligned} & \prod_{k=0}^{m-1} (\omega_m^k + 3 + \omega_m^{-k}) \\ =& \prod_{k=0}^{m-1} (\omega_m^{2k} + 3 \omega_m^k + 1) \\ =& \prod (\omega_m^k - r_1) (\omega_m^k - r_2) & r_{1,2} = \frac {- 3 \pm \sqrt 5} 2 \\ =& (r_1^m - 1) (r_2^m - 1) \\ =& 2 - r_1^m - r_2^m & r_1 r_2 = 1 \\ =& 2 + (-r_1)^m + (-r_2)^m \\ \end{aligned}\]现在只要证明它永远是整数:
\[\sqrt{\frac {2 + (-r_1)^m + (-r_2)^m} 5}\]注意到
\[\frac {3 \pm \sqrt 5} 2 = \left( \frac {1 \pm \sqrt 5} 2 \right)^2\]设 $\varphi = \frac {1 + \sqrt 5} 2, \psi = \frac {1 - \sqrt 5} 2$,$F$ 为 Fibonacci 数:
\[\begin{aligned} & \sqrt{\frac {2 + (-r_1)^m + (-r_2)^m} 5} \\ =& \frac 1 {\sqrt 5} \sqrt{2 + \varphi^{2m} + \psi^{2m}} \\ =& \frac 1 {\sqrt 5} (\varphi^m + \psi^m) \\ =& F_m = \boxed{F_{2n+1}} \end{aligned}\]Example 5.24 AIME I 2023 #15
找到最大的质数 $p < 1000$,使得存在一个复数 $z$ 满足:
- $z$ 的实部和虚部是整数。
- $\lvert z \rvert = \sqrt p$。
- 存在一个三角形的三边分别为 $p, \Re(z^3), \Im(z^3)$。
不妨设 $z = a + bi$,则 $a^2 + b^2 = p$。
$z^3 = (a^3 - 3 a b^2) + i (3 a^2 b - b^3)$
\[\begin{cases} a^3 - 3 a b^2 > 0 \\ 3 a^2 b - b^3 > 0 \\ \end{cases}\] \[\lvert (a + b) (a^2 - 4 a b + b^2) \rvert < p < (a - b) (a^2 + 4 a b + b^2)\] \[\lvert a + b \rvert \lvert a^2 + b^2 - 4ab \rvert < a^2 + b^2\]WLOG 设 $a > b$
TODO: