转动惯量与几何
Published:
Stewart 定理
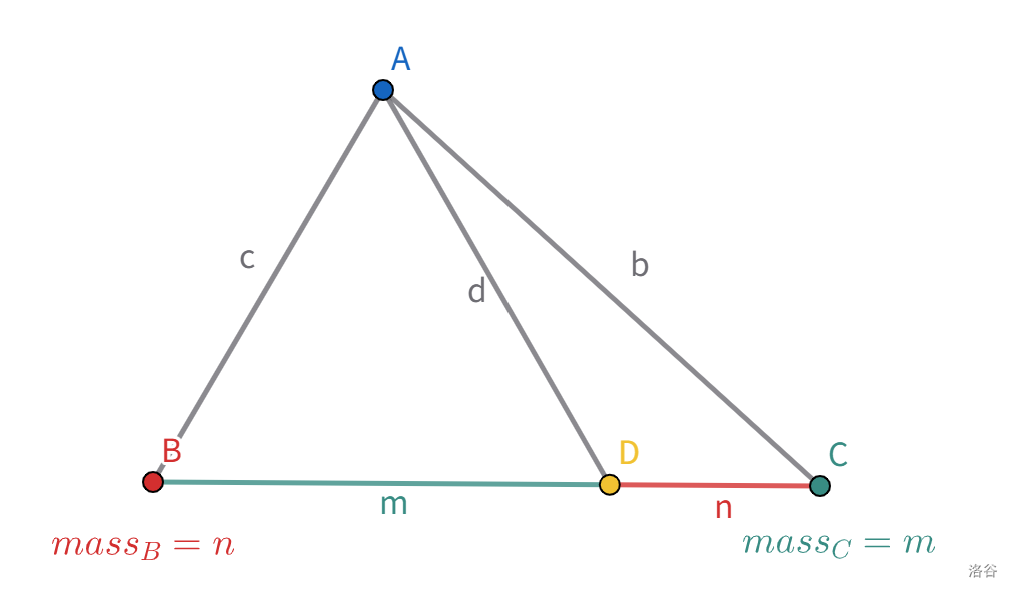
根据 $b,c,m,n$,求出 $d$:
在点 $B$ 处放一个质量为 $n$ 的质点,在点 $C$ 处放一个质量为 $m$ 的质点。可以发现这个质点系的质心在 $D$。
写出该质点系对质心的转动惯量:
\[I_{CM} = m n^2 + m^2 n = mn(n+m)\]写出该质点系对 $A$ 的转动惯量:
\[I = b^2 m + c^2 n\]对这两个转动惯量使用平行轴定理:
\[I = I_{CM} + (m+n) d^2\] \[\boxed{ b^2 m + c^2 n = (m+n) (d^2 + mn) }\]进一步思考,甚至可以得到 Stewart 定理与质点系的平行轴定理等价。对一个 $n$ 个点的质点系进行归纳,先把前 $n-1$ 个质点的质量等效在质心,将这个质心与第 $n$ 个质点使用 Stewart 定理即可。
重心到三角形顶点距离平方和
练习题:Example 5.22 AIME I 2012 #14
在三角形 $ABC$ 中,重心为 $G$,则:
\[\boxed{ GA^2 + GB^2 + GC^2 = \frac 1 3 (a^2 + b^2 + c^2) }\]对于一个任意点 $P$:
\[\boxed{ PA^2 + PB^2 + PC^2 \ge \frac 1 3 (a^2 + b^2 + c^2) }\]取等当且仅当 $P$ 是重心 $G$。
证明
在 $A,B,C$ 处各放置一个质量为 $1$ 的质点。
计算质心 $G$ 处转动惯量:
\[I_G = GA^2 + GB^2 + GC^2\]使用三次平行轴定理:
\[\begin{cases} I_A = I_G + 3 GA^2 = b^2 + c^2 \\ I_B = I_G + 3 GB^2 = a^2 + c^2 \\ I_C = I_G + 3 GC^2 = a^2 + b^2 \\ \end{cases}\] \[\begin{aligned} 6 (GA^2 + GB^2 + GC^2) &= 2 (a^2 + b^2 + c^2) \\ GA^2 + GB^2 + GC^2 &= \frac 1 3 (a^2 + b^2 + c^2) \end{aligned}\]得证。
进一步地,对于任意一点 $P$,有
\[PA^2 + PB^2 + PC^2 = I_P = I_G + 3 PG^2 \ge I_G\]取等当且仅当 $PG = 0$,即 $P$ 就是 $G$。