反演变换
Published:
反演变换
给定一个圆 $\omega$ 及其圆心 $O$,还有半径 $r$。点 $P$ 关于 $\omega$ 的反演点 $P’$ 被定义为:在射线 $OP$ 上,且满足以下条件的点
\[OP \times OP' = R^2\]对于任意的两点 $A,B$ 及反演后的 $A’,B’$,可以轻松导出如下相似三角形:
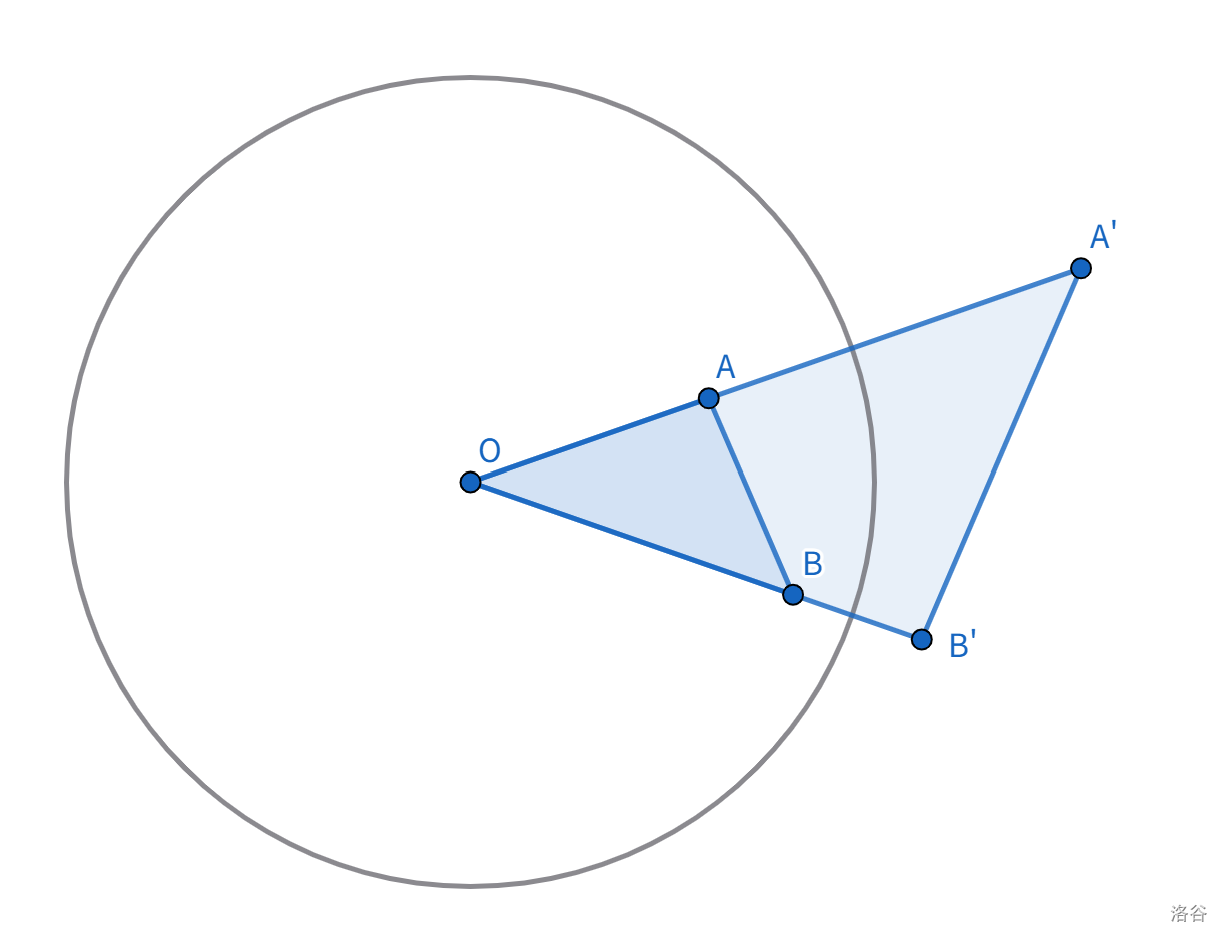
并且线段 $A’B’$ 的长度和线段 $AB$ 的长度有如下的数量关系:
\[A'B' = \frac {OB'} {OA} \times AB\]把 $OB’$ 用 $OB$ 表示,更对称:
\[\boxed{ A'B' = \frac {R^2} {OA \times OB} \times AB }\]直线的反演
经过 $O$ 的直线反演后是自身,这是平凡的。接下来只关心不经过 $O$ 的情况。
对不经过 $O$ 的直线 $l$ 上的所有点反演,得到的轨迹是什么?
作 $OA \perp l$ 垂足为 $A$。令 $A$ 的反演点为 $A’$。在直线上任找一个点 $B$,令 $B$ 的反演点为 $B’$。
构造刚才的相似三角形,可知 $\angle OB’A’ = \angle OAB$ 是直角。因此 $B’$ 在以 $OA’$ 为直径的圆 $\omega$ 上。
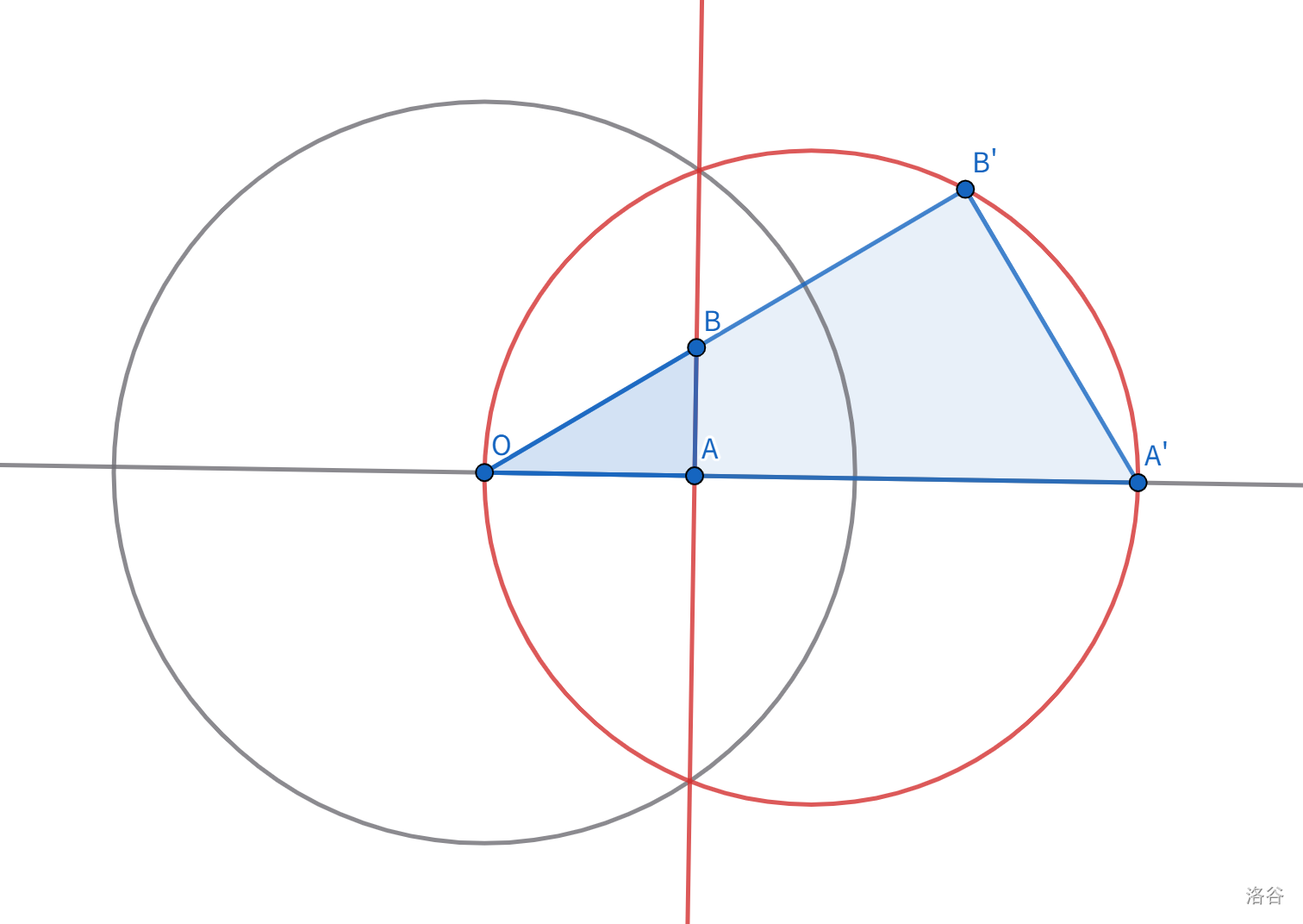
此时已经证明 $B \mapsto B’$ 可以把 $l$ 映射到 $\omega$ 的一个子集。那么这是一个双射吗?
这“几乎”是一个双射。对于任意一个圆上的点 $B’$,连结 $OB’$ 与 $l$ 交于 $B$ 即可。
但是若我们选择的 $B’ = O$ 则这会失效!这是不优美的,我们要改进这一点。从代数上说 $OB’ = 0$ 说明 $OB = \infty$,若我们引入无穷远点 $\infty$,则我们可以认为 $B’$ 对应的原来的点为 $\infty$。也就是说,我们的世界从欧氏平面变为了 Riemann 球。
现在我们可以说:在 Riemann 球上,不经过 $O$ 的直线反演结果为一个经过 $O$ 的圆。
圆的反演
根据反演变换可逆,经过 $O$ 的圆反演后是一条不经过 $O$ 的直线。
对不经过 $O$ 的圆反演结果是什么?
是不经过 $O$ 的另一个圆。
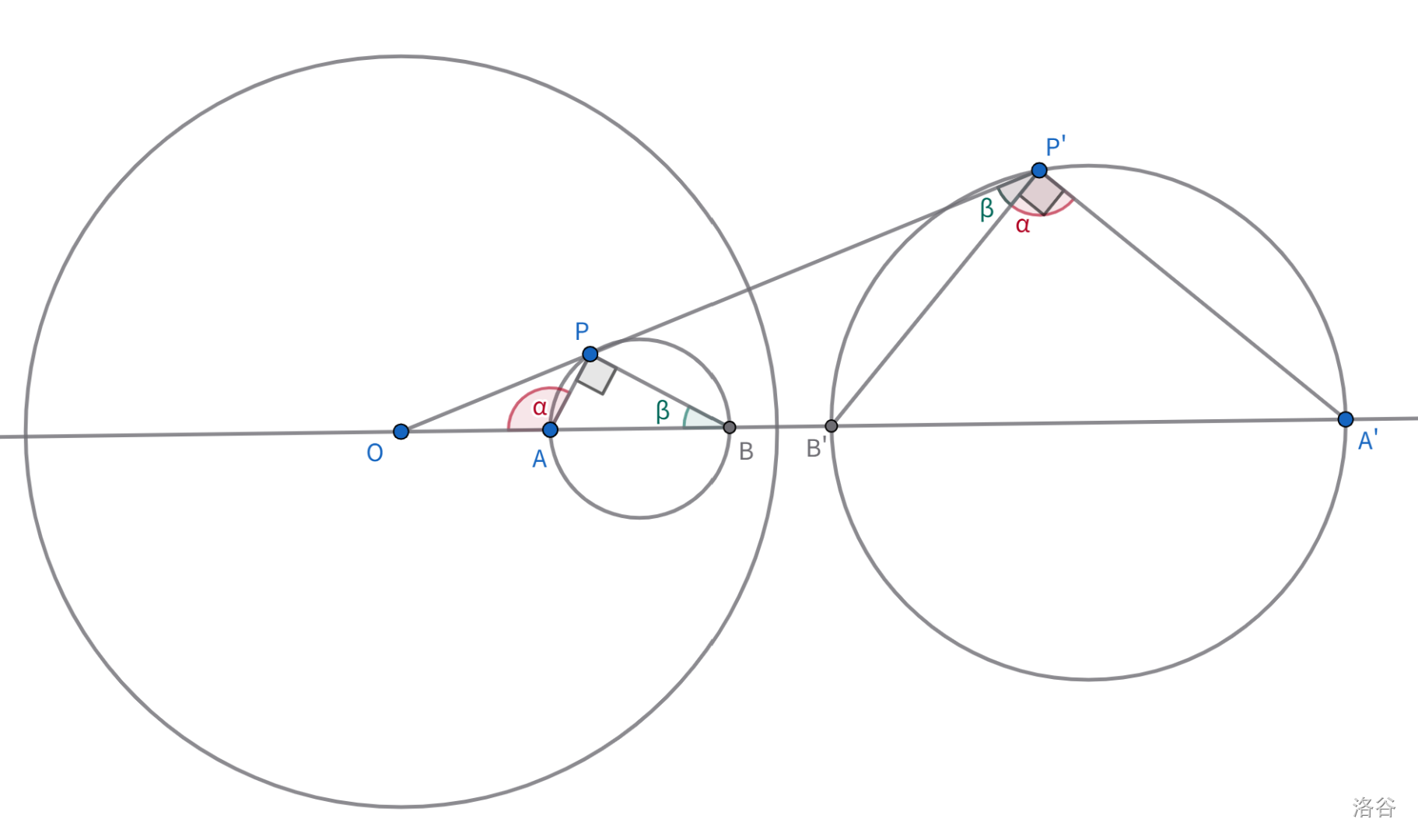
广义圆
我们发现「直线和圆」对反演变换是封闭的。因此我们把它俩合称广义圆。直线可以被视为半径无穷大、圆心在 $\infty$ 的圆。
经过 $O$ 的广义圆在反演后经过 $\infty$;经过 $\infty$ 的广义圆在反演后经过 $O$。
Ptolemy 定理
欧氏距离的三角形不等式,有没有对应的反演后的定理?
对于 $A,B,C$ 三点,设反演点为 $A’,B’,C’$,它们应该满足三角形不等式:
\[A'B' + B'C' \ge A'C'\]用反演前的距离换算:
\[\begin{aligned} \frac {R^2} {OA \times OB} \times AB + \frac {R^2} {OB \times OC} \times BC &\ge \frac {R^2} {OA \times OC} \times AC \\ OC \times AB + OA \times BC &\ge OB \times AC \end{aligned}\]把 $O$ 换个字母换成 $D$,再整理一下:
\[\boxed{ AB \times CD + AD \times BC \ge AC \times BD }\]这个结论被称为 Ptolemy 不等式。
取等条件呢?三角不等式的取等条件为 $A’, B’, C’$ 共线且 $B’$ 在 $A’,C’$ 之间,反演回来就是 $A,B,C,O$ 共圆形成四边形。
因此,对于圆内接四边形 $ABCD$,有:
\[\boxed{ AB \times CD + AD \times BC = AC \times BD }\]这个结论被称为 Ptolemy 定理。
与复变函数的关系
不妨设反演圆为单位圆。复数 $z$ 对应的点在反演后对应的复数即为:
\[z \mapsto \frac 1 {\bar z}\]因此,作为一个解析映射,在除了 $O$ 以外的地方($O$ 处不解析),它是一个保角变换。相切可以看成夹角为 $0$,因此反演也保持相切关系不变。